8.4: La teoría orbital molecular
- Page ID
- 1865
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Habilidades para desarrollar
- Resumir el enfoque mecánico cuántico básico para derivar los orbitales moleculares de los orbitales atómicos.
- Describir las características de los orbitales moleculares de unión y antienlace.
- Calcular órdenes de enlace basadas en configuraciones de electrones moleculares
- Escribir configuraciones de electrones moleculares para moléculas diatómicas de primera y segunda fila
- Relacionar estas configuraciones de electrones con la estabilidad de las moléculas y sus propiedades magnéticas.
Para casi todas las moléculas covalentes que existen, ahora podemos dibujar la estructura de Lewis, predecir la geometría de los pares de electrones, predecir la geometría molecular y acercarnos a la predicción de los ángulos de enlace. Sin embargo, una de las moléculas más importantes que conocemos, la molécula del oxígeno O2, presenta un problema con respecto a su estructura de Lewis. Escribiríamos la siguiente estructura de Lewis para O2:
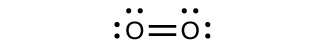
Esta estructura electrónica se adhiere a todas las reglas que rigen la teoría de Lewis. Hay un enlace doble O = O, y cada átomo de oxígeno tiene ocho electrones a su alrededor. Sin embargo, esta imagen está en desacuerdo con el comportamiento magnético del oxígeno. Por sí mismo, el O2 no es magnético, pero se siente atraído por los campos magnéticos. Por lo tanto, cuando vertimos el oxígeno líquido a través de un imán fuerte, se acumula entre los polos del imán y desafía la gravedad. Tal atracción hacia un campo magnético se llama el paramagnetismo, y surge en moléculas que tienen electrones no apareados. Y, sin embargo, la estructura de Lewis del O2 indica que todos los electrones están emparejados. ¿Cómo explicamos esta discrepancia?
La susceptibilidad magnética mide la fuerza experimentada por una sustancia en un campo magnético. Cuando comparamos el peso de una muestra con el peso medido en un campo magnético (Figura \(\PageIndex{1}\)), las muestras paramagnéticas que son atraídas por el imán aparecerán más pesadas debido a la fuerza ejercida por el campo magnético. Podemos calcular el número de electrones no apareados en función del aumento de peso.
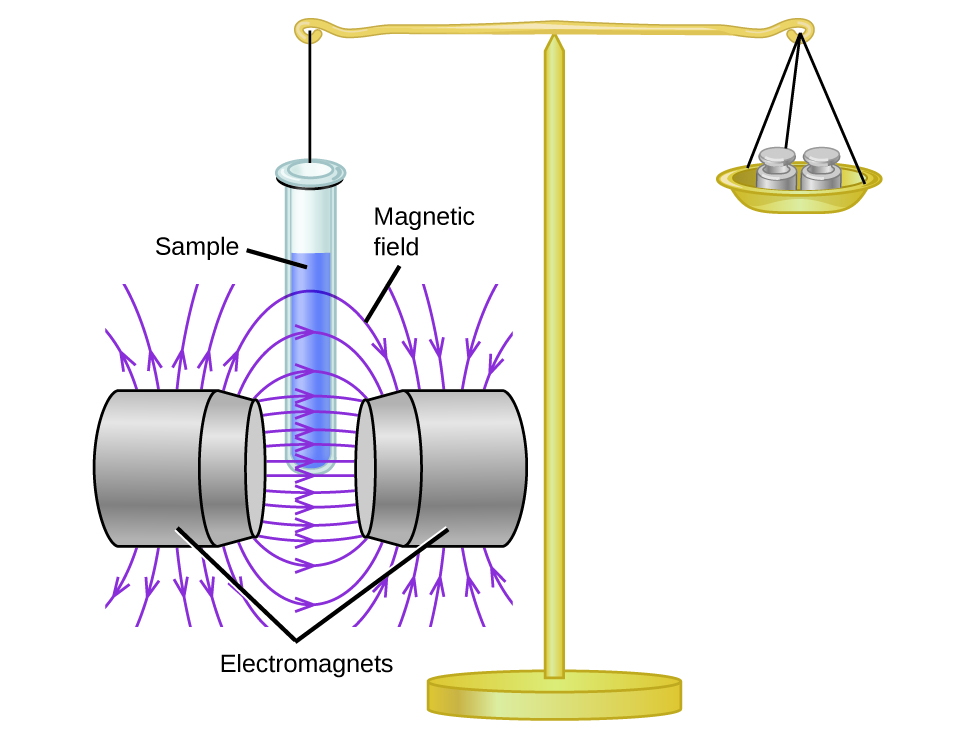
Los experimentos muestran que cada molécula de O2 tiene dos electrones no apareados. El modelo de estructura de Lewis no predice la presencia de estos dos electrones no apareados. A diferencia del oxígeno, el peso aparente de la mayoría de las moléculas es un poco menos en la presencia de un campo magnético no homogéneo. Los materiales en los que todos los electrones están emparejados son diamagnéticos y repelen un campo magnético. Los materiales paramagnéticos y diamagnéticos no actúan como imanes permanentes. Solo en la presencia de un campo magnético aplicado demuestran atracción o repulsión.
Video \(\PageIndex{1}\): El agua, como la mayoría de las moléculas, contiene todos los electrones emparejados. Los seres vivos contienen un gran porcentaje de agua, por eso demuestra un comportamiento diamagnético. Si coloca una rana cerca de un imán suficientemente grande, levitará. Puedes ver videos de ranas flotantes diamagnéticas, fresas y más (https://www.youtube.com/watch?v=A1vyB-O5i6E)
La teoría de la órbita molecular (teoría MO) nos da una explicación del enlace químico que explica el paramagnetismo de la molécula del oxígeno. También explica el enlace en una serie de otras moléculas, como violaciones de la regla del octeto y más moléculas con enlaces más complicados (más allá del alcance de este texto) que son difíciles de describir con las estructuras de Lewis. Además, proporciona un modelo para describir las energías de los electrones en una molécula y la ubicación probable de estos electrones. A diferencia de la teoría del enlace de valencia, que usa orbitales híbridos que se asignan a un átomo específico, la teoría MO usa la combinación de orbitales atómicos para producir orbitales moleculares que se deslocalizan sobre la molécula completa en lugar de localizarse en sus átomos constituyentes. La teoría MO también nos ayuda a comprender por qué algunas sustancias son conductores eléctricos, otras son semiconductores y otras son aislantes. La tabla \(\PageIndex{1}\) resume los puntos principales de las dos teorías de enlace complementarias. Ambas teorías proporcionan formas diferentes y útiles de describir la estructura molecular.
| Teoría del enlace de valencia | Teoría orbital molecular |
|---|---|
| considera los enlaces como localizados entre un par de átomos | considera electrones deslocalizados en toda la molécula |
|
crea enlaces a partir de la superposición de orbitales atómicos(s, p, d…) y orbitales híbridos (sp, sp2, sp3…) |
combina orbitales atómicos para formar orbitales moleculares (σ, σ*, π, π*) |
| forma enlaces σ o π | crea interacciones de unión y antienlace en función de qué orbitales se llenan |
| predice la forma molecular en función del número de regiones de densidad electrónica | predice la disposición de los electrones en las moléculas |
| necesita múltiples estructuras para describir la resonancia |
La teoría de los orbitales moleculares describe la distribución de los electrones en las moléculas de la misma manera que la distribución de electrones en los átomos se describe usando los orbitales atómicos. Usando la mecánica cuántica, el comportamiento de un electrón en una molécula todavía se describe mediante una función de onda, Ψ, análoga al comportamiento en un átomo. Al igual que los electrones alrededor de los átomos aislados, los electrones alrededor de los átomos en las moléculas están limitados a energías discretas (cuantificadas). La región del espacio en la que es probable que se encuentre un electrón de valencia en una molécula se llama el orbital molecular (Ψ2). Al igual que un orbital atómico, un orbital molecular está lleno cuando contiene dos electrones con espín opuesto.
Consideraremos los orbitales moleculares en moléculas compuestas de dos átomos idénticos (H2 o Cl2, por ejemplo). Estas moléculas se llaman las moléculas diatómicas homonucleares. En estas moléculas diatómicas, se producen varios tipos de orbitales moleculares.
El proceso matemático de combinar orbitales atómicos para generar orbitales moleculares se llama la combinación lineal de los orbitales atómicos (LCAO). La función de onda describe las propiedades ondulatorias de un electrón. Los orbitales moleculares son combinaciones de funciones de ondas orbitales atómicas. La combinación de ondas puede conducir a una interferencia constructiva, en la que los picos se alinean con los picos, o la interferencia destructiva, en la que los picos se alinean con los puntos más bajos (Figura \(\PageIndex{2}\)). En los orbitales, las ondas son tridimensionales y se combinan con ondas en fase que producen regiones con una mayor probabilidad de densidad electrónica y nodos fuera de fase que producen ondas, o regiones sin densidad de electrones.

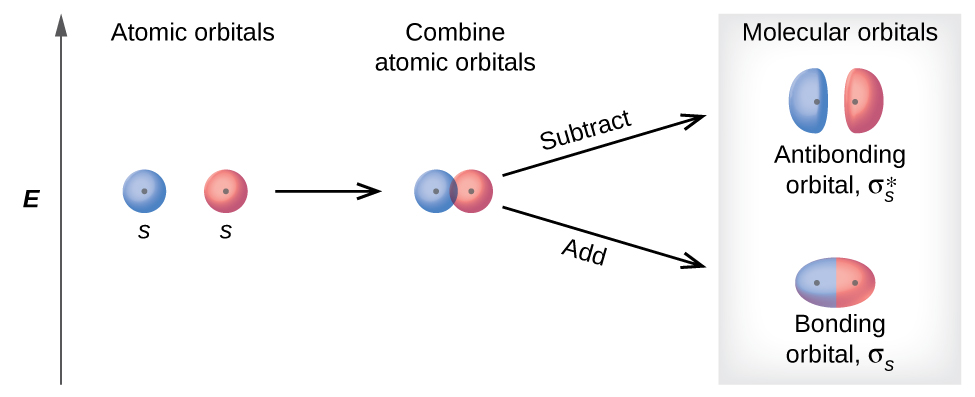
Hay dos tipos de orbitales moleculares que se pueden formar a partir de la superposición de dos orbitales atómicos en átomos adyacentes. Los dos tipos se ilustran en la figura 8.4.3. La combinación en fase produce un orbital molecular σs de menor energía (leído como "sigma-s") en el que la mayor parte de la densidad electrónica está directamente entre los núcleos. La adición fuera de fase (que también se puede considerar como restando las funciones de onda) produce un orbital molecular de mayor energía \(σ^∗_s\) (leído como "sigma-s-estrella") en el que existe es un nodo entre los núcleos. El asterisco significa que el orbital es un orbital de antienlace. Los electrones en un orbital σs son atraídos por ambos núcleos al mismo tiempo y son más estables (de menor energía) de lo que serían como átomos aislados. Agregar electrones a estos orbitales crea una fuerza que mantiene los dos núcleos unidos, por lo que los llamamos los orbitales de unión. Los electrones en los orbitales \(σ^∗_s \) están ubicados muy lejos de la región entre los dos núcleos. La fuerza de atracción entre los núcleos y estos electrones separa los dos núcleos. Por lo tanto, estos orbitales se llaman los orbitales de antienlace. Los electrones llenan el orbital de enlace de menor energía antes que el orbital de antienlace de mayor energía, así como llenan los orbitales atómicos de menor energía antes de llenar los orbitales atómicos de mayor energía.
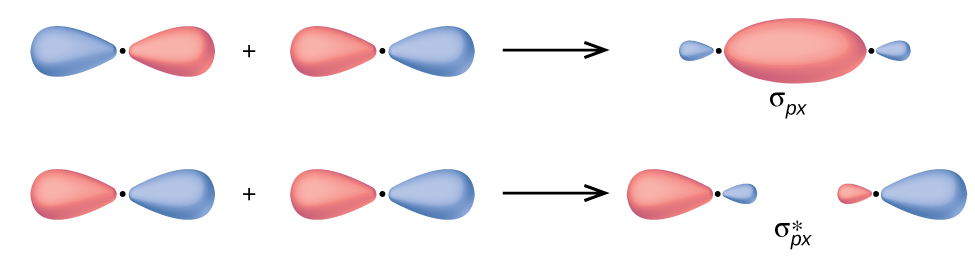
En los orbitales p, la función de onda da lugar a dos lóbulos con fases opuestas, análogamente a cómo una onda bidimensional tiene ambas partes por encima y por debajo del promedio. Indicamos las fases por sombreando los lóbulos orbitales de diferentes colores. Cuando los lóbulos orbitales de la misma fase se superponen, la interferencia de onda constructiva aumenta la densidad de electrones. Cuando las regiones de la fase opuesta se superponen, la interferencia destructiva de la onda disminuye la densidad de electrones y crea nodos. Cuando los orbitales p se superponen de extremo a extremo, crean orbitales σ y σ* (Figura \(\PageIndex {4}\)). Si dos átomos se encuentran a lo largo del eje x en un sistema de coordenadas cartesianas, los dos orbitales px se superponen de extremo a extremo y forman σpx (enlace) y \(σ^∗_{px}\) (antienlace) (leído como "sigma-p-x” y “sigma-p-x estrella", respectivamente). Al igual que con la superposición s-orbital, el asterisco indica el orbital con un nodo entre los núcleos, que es un orbital antienlace de mayor energía.
La superposición lado a lado de dos orbitales p da lugar a un orbital molecular de unión pi(π) y a un orbital molecular antienlace π*, como se muestra en la Figura \(\PageIndex{5}\). En la teoría del enlace de valencia, describimos los enlaces π como enlaces que contienen un plano nodal que contiene el eje internuclear y perpendicular a los lóbulos de los orbitales p, con densidad de electrones a cada lado del nodo. En la teoría de los orbitales moleculares, describimos el orbital π por esta misma forma, y existe un enlace π cuando este orbital contiene electrones. Los electrones en este orbital interactúan con ambos núcleos y ayudan a mantener los dos átomos juntos, convirtiéndolo en un orbital de enlace. Para la combinación desfasada, se crean dos planos nodales, uno a lo largo del eje internuclear y otro perpendicular entre los núcleos.
Figure \(\PageIndex{5}\): La superposición lado a lado de cada uno de los dos orbitales da como resultado la formación de dos orbitales moleculares π. La combinación de los orbitales fuera de fase da como resultado un orbital molecular de antienlace con dos nodos. Uno contiene el eje internuclear, y el otro es perpendicular al eje. La combinación de los orbitales en fase da como resultado un orbital de unión. Hay un nodo (plano azul) que contiene el eje internuclear con los dos lóbulos del orbital ubicados arriba y debajo de este nodo.
En los orbitales moleculares de las moléculas diatómicas, cada átomo también tiene dos grupos de orbitales p orientados uno al lado del otro (py y pz), por lo que estos cuatro orbitales atómicos se combinan en pares para formar dos orbitales π y dos orbitales π*. Los orbitales πpy y \(π^∗_{py}\) están orientados en ángulo recto con los orbitales πpz y \(π^∗_{pz}\) Excepto por su orientación, los orbitales πpy y πpz son idénticos y tienen la misma energía; son orbitales degenerados. Los orbitales de antienlace \(π^∗_{py}\) y \(π^∗_{pz}\) también son degenerados e idénticos, excepto por su orientación. Un total de seis orbitales moleculares resulta de la combinación de los seis orbitales p atómicos en dos átomos: σpx y \(σ^∗_{px}\), πpy y \(π^∗_{py}\), πpz y \(π^∗_{pz}\).
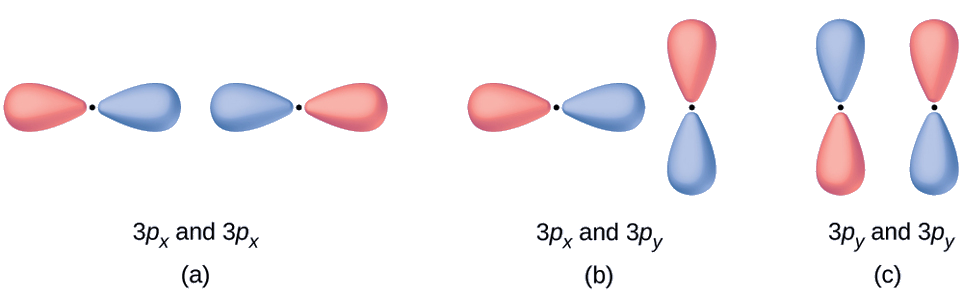
Ejemplo \(\PageIndex{1}\)
Los orbitales moleculares predicen qué tipo (si lo hay) de orbital molecular resultaría de agregar las funciones de onda para que cada par de orbitales se superpongan. Todos los orbitales tienen energías similares.
Solución
a. Esta es una combinación en fase, que resulta en un orbital σ3p
b. Esto no dará como resultado un nuevo orbital porque el componente en fase (parte inferior) y el componente fuera de fase (parte superior) se cancelan. Solo los orbitales con la alineación correcta se pueden combinar.
c. Esta es una combinación desfasada, que resulta en un orbital \(π^∗_{3p}\)
Ejercicio \(\PageIndex{1}\)
Etiquete el orbital molecular que se muestra como σ o π, enlace o antienlace e indique dónde se produce el nodo.

- Respuesta
-
El orbital está ubicado a lo largo del eje internuclear, por lo que es un orbital σ. Hay un nodo que divide el eje internuclear en dos partes, por lo que es un orbital de antienlace.

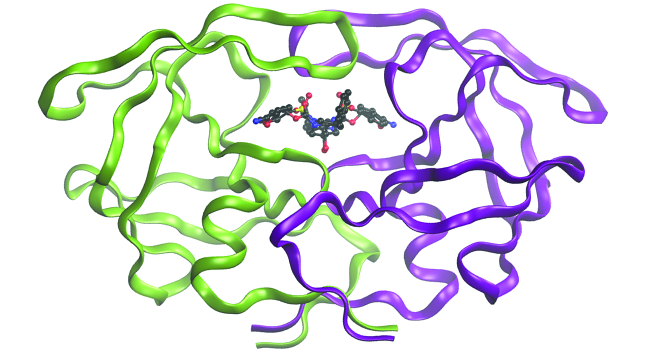
Aplicación: la química computacional en el diseño de las drogas
Aunque las descripciones de los enlaces descritas en este capítulo involucran muchos conceptos teóricos, también tienen muchas aplicaciones prácticas del mundo real. Por ejemplo, el diseño de medicamentos es un campo importante que usa nuestra comprensión de los enlaces químicos para desarrollar productos farmacéuticos. Esta área de estudio interdisciplinaria usa la biología (comprensión de las enfermedades y cómo funcionan) para identificar objetivos específicos, como un sitio de unión que está involucrado en una vía de enfermedad. Al modelar las estructuras del sitio de unión y los medicamentos potenciales, los químicos computacionales pueden predecir qué estructuras pueden encajar y que efectivamente se unirán (Figura \(\PageIndex{6}\)). Miles de candidatos potenciale se pueden reducir a algunos de los candidatos más prometedores. Estas moléculas candidatas se prueban cuidadosamente para determinar los efectos secundarios, la eficacia con la que se pueden transportar a través del cuerpo y otros factores. Se han descubierto docenas de nuevos productos farmacéuticos importantes con la ayuda de la química computacional, y se están realizando nuevos proyectos de investigación.
Diagramas de energía orbital molecular
Los niveles de energía relativos de los orbitales atómicos y moleculares se muestran típicamente en un diagrama de orbitales moleculares (Figura \(\PageIndex{7}\)). Para una molécula diatómica, los orbitales atómicos de un átomo se muestran a la izquierda y los del otro átomo se muestran a la derecha. Cada línea horizontal representa un orbital que puede contener dos electrones. Los orbitales moleculares formados por la combinación de los orbitales atómicos se muestran en el centro. Las líneas discontinuas muestran cuáles de los orbitales atómicos se combinan para formar los orbitales moleculares. Para cada par de orbitales atómicos que se combinan, un orbital molecular de energía más baja (enlace) y un resultado orbital de energía más alta (antienlace). Por lo tanto, podemos ver que la combinación de los seis orbitales atómicos de 2p da como resultado tres orbitales de enlace (uno σ y dos π) y tres orbitales de antienlace (uno σ* y dos π*).
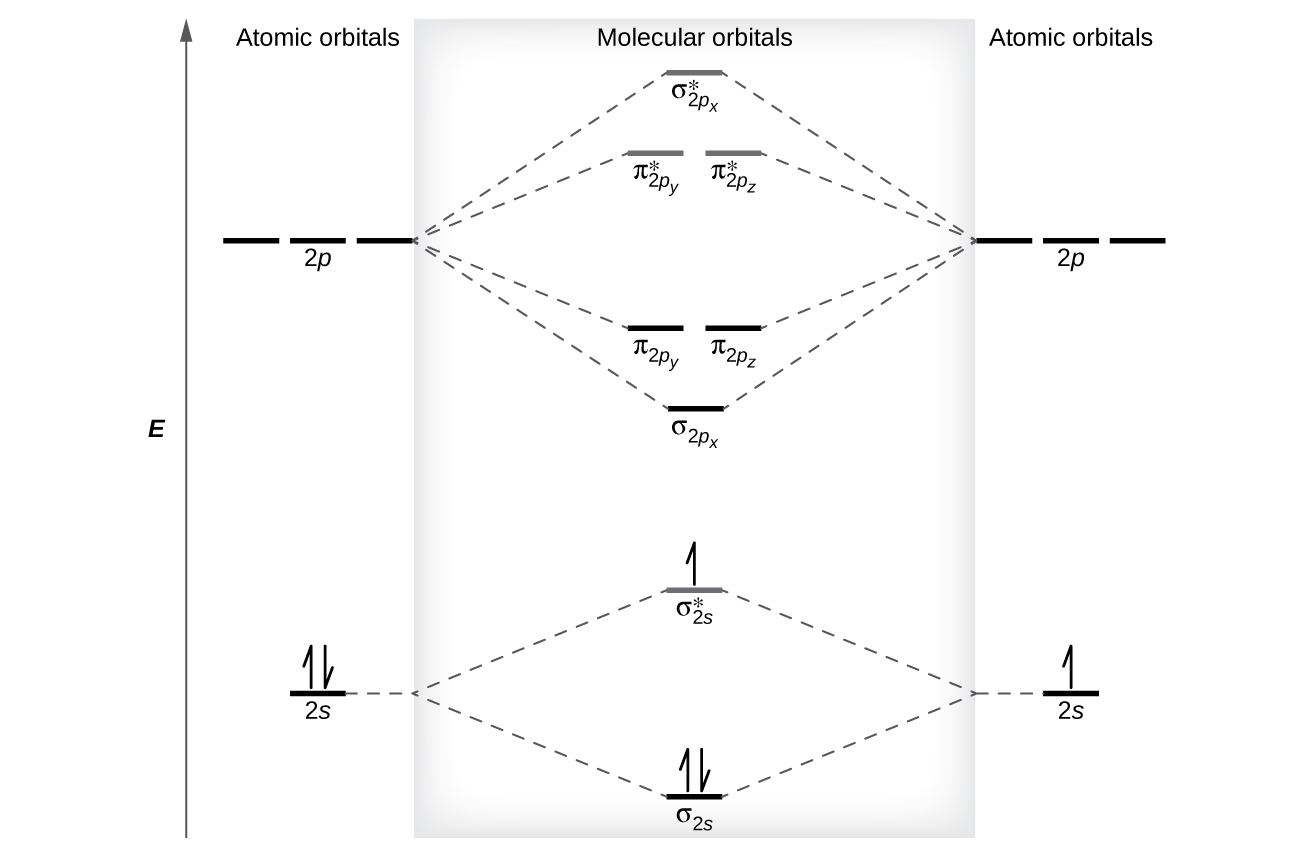
Predecimos la distribución de electrones en estos orbitales moleculares llenando los orbitales de la misma manera que llenamos los orbitales atómicos, según el principio de Aufbau. Los orbitales de energía baja se llenan primero, los electrones se extienden entre los orbitales degenerados antes del emparejamiento, y cada orbital puede contener un máximo de dos electrones con espines opuestos (Figura \(\PageIndex{7}\)). Del mismo modo que escribimos las configuraciones electrónicas para átomos, podemos escribir la configuración electrónica molecular enumerando los orbitales con superíndices que indican la cantidad de electrones presentes. Para mayor claridad, colocamos paréntesis alrededor de los orbitales moleculares con la misma energía. En este caso, cada orbital tiene una energía diferente, por lo que los paréntesis separan cada orbital. Por lo tanto, esperaríamos que una molécula o ion diatómico que contiene siete electrones (como \(\ce{Be2+}\)) tuviera la configuración de electrones moleculares \((σ_{1s})^2(σ^∗_{1s})^2(σ_{2s})^2(σ^∗_{2s})^1\). Es común omitir los electrones centrales de los diagramas y configuraciones de los orbitales moleculares e incluir solo los electrones de valencia.
El orden de enlace
El diagrama de orbitales moleculares llenos muestra el número de electrones en los orbitales moleculares de enlace y antienlace. La contribución neta de los electrones a la fuerza de enlace de una molécula se identifica determinando el orden de enlace que resulta del llenado de los orbitales moleculares por los electrones.
Cuando usamos las estructuras de Lewis para describir la distribución de electrones en las moléculas, definimos el orden de enlace como el número de pares de electrones de enlace entre dos átomos. Por lo tanto, un enlace simple tiene un orden de enlace de 1, un enlace doble tiene un orden de enlace de 2 y un enlace triple tiene un orden de enlace de 3. Definimos el orden de enlace de manera diferente cuando usamos la descripción molecular orbital de la distribución de electrones, pero el orden de enlace resultante suele ser el mismo. La técnica MO es más precisa y puede explicar casos cuando falla el método de estructura de Lewis, pero ambos métodos describen el mismo fenómeno.
En el modelo orbital molecular, un electrón contribuye a una interacción de enlace si ocupa un orbital de enlace y contribuye a una interacción de antienlace si ocupa un orbital de antienlace. El orden de enlace se calcula por restando los electrones desestabilizadores (antienlaces) de los electrones estabilizadores (enlaces). Ya que un enlace consiste en dos electrones, dividimos por dos para obtener el orden de enlace. Podemos determinar el orden de los enlace con la siguiente ecuación:
El orden de un enlace covalente es una guía para su fuerza; un enlace entre dos átomos dados se vuelve más fuerte a medida que aumenta el orden del enlace. Si la distribución de los electrones en los orbitales moleculares entre dos átomos es tal que el enlace resultante tendría un orden de enlace de cero, no se forma un enlace estable. A continuación, veremos algunos ejemplos específicos de los diagramas de MO y los órdenes de enlaces.
Los enlaces en las moléculas diatómicas
Una molécula de dihidrógeno (H2) se forma a partir de dos átomos de hidrógeno. Cuando los orbitales atómicos de los dos átomos se combinan, los electrones ocupan el orbital molecular de menor energía, el orbital de enlace σ1s. Una molécula de dihidrógeno, H2, se forma fácilmente porque la energía de una molécula H2 es más baja que la de dos átomos de H. El orbital σ1s que contiene ambos electrones es más bajo en energía que cualquiera de los dos orbitales atómicos 1s.
Un orbital molecular puede contener dos electrones, por lo que ambos electrones en la molécula H2 están en el orbital de enlace σ1s; la configuración electrónica es \((σ_{1s})^2\). Representamos esta configuración usando un diagrama de energía orbital molecular (Figura \(\PageIndex{8}\)) en el que una sola flecha hacia arriba indica un electrón en un orbital, y dos flechas (hacia arriba y hacia abajo) indican dos electrones de espín opuesto.
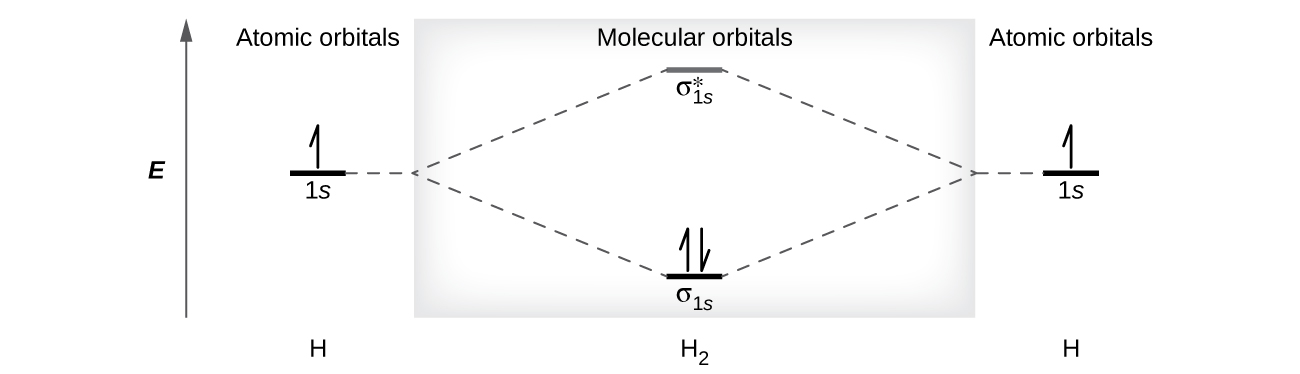
Una molécula de dihidrógeno contiene dos electrones en enlace y no contiene electrones de antienlace, por lo que tenemos
\[\ce{bond\: order\: in\: H2}=\dfrac{(2−0)}{2}=1\]
Debido a que el orden de enlace para el enlace H – H es uno, el enlace es un enlace simple.
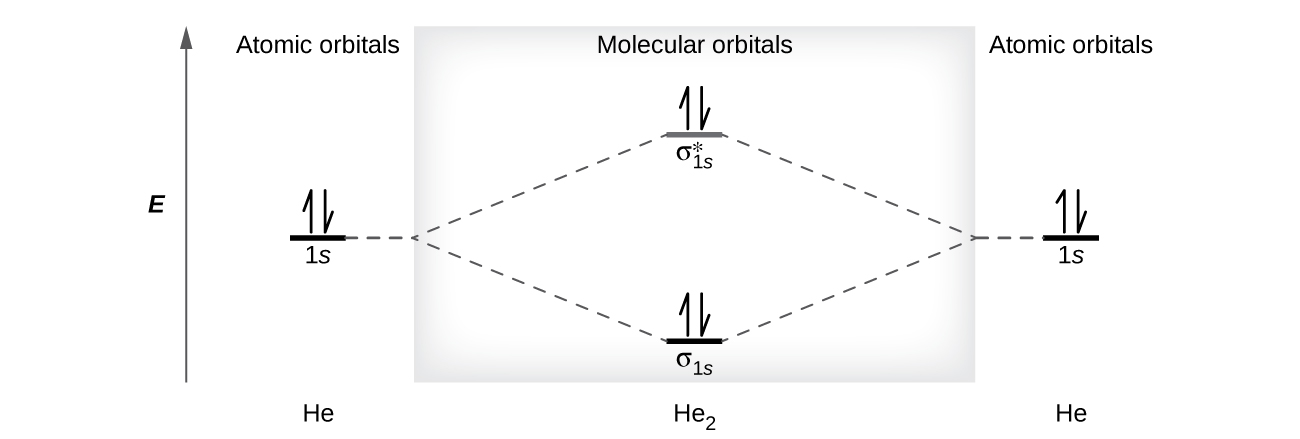
Un átomo de helio tiene dos electrones, los cuales están en su orbital 1s. Dos átomos de helio no se combinan para formar una molécula de dihelio, He2, con cuatro electrones, porque el efecto estabilizador de los dos electrones en el orbital de enlace de baja energía se compensaría con el efecto desestabilizador de los dos electrones de antienlace de alta energía en el orbital molecular. Escribiríamos la configuración electrónica hipotética de He2 como \((σ_{1s})^2(σ^∗_{1s})^2\) como en la Figura \(\PageIndex{9}\). El cambio neto de energía sería cero, por lo que no hay fuerza impulsora para que los átomos de helio formen la molécula diatómica. De hecho, el helio existe como átomos discretos más que como moléculas diatómicas. El orden de enlace en una molécula hipotética de dihelio sería cero.
Un orden de enlace de cero indica que no se forma ningún enlace entre dos átomos.
Las moléculas diatómicas del segundo período
Ocho posibles moléculas diatómicas homonucleares podrían estar formadas por los átomos del segundo período de la tabla periódica: Li2, Be2, B2, C2, N2, O2, F2, y Ne2. Sin embargo, podemos predecir que la molécula Be2 y la molécula Ne2 no serían estables. Podemos predecir esto considerando las configuraciones de los electrones moleculares (Tabla \(\PageIndex{1}\)).
| Molecula | Configuración de Electrones | Orden de enlace |
|---|---|---|
| Li2 | \((σ_{2s})^2\) | 1 |
| Be2 (inestable) | \((σ_{2s})^2(σ^∗_{2s})^2\) | 0 |
| B2 | \((σ_{2s})^2(σ^∗_{2s})^2(π_{2py},\:π_{2pz})^2\) | 1 |
| C2 | \((σ_{2s})^2(σ^∗_{2s})^2(π_{2py},\:π_{2pz})^4\) | 2 |
| N2 | \((σ_{2s})^2(σ^∗_{2s})^2(π_{2py},\:π_{2pz})^4(σ_{2px})^2\) | 3 |
| O2 | \((σ_{2s})^2(σ^∗_{2s})^2(σ_{2px})^2(π_{2py},\:π_{2pz})^4(π^∗_{2py},π^∗_{2pz})^2\) | 2 |
| F2 | \((σ_{2s})^2(σ^∗_{2s})^2(σ_{2px})^2(π_{2py},\:π_{2pz})^4(π^∗_{2py},\:π^∗_{2pz})^4\) | 1 |
| Ne2 (inestable) | \((σ_{2s})^2(σ^∗_{2s})^2(σ_{2px})^2(π_{2py},\:π_{2pz})^4(π^∗_{2py},π^∗_{2pz})^4(σ^∗_{2px})^2\) | 0 |
Predecimos configuraciones de los electrones orbitales moleculares de valencia tal como predecimos configuraciones electrónicas de átomos. Los electrones de valencia se asignan a orbitales moleculares de valencia con las energías más bajas posibles. De acuerdo con la regla de Hund, cada vez que hay dos o más orbitales moleculares degenerados, los electrones llenan cada orbital de ese tipo individualmente antes de que pase un emparejamiento de electrones.
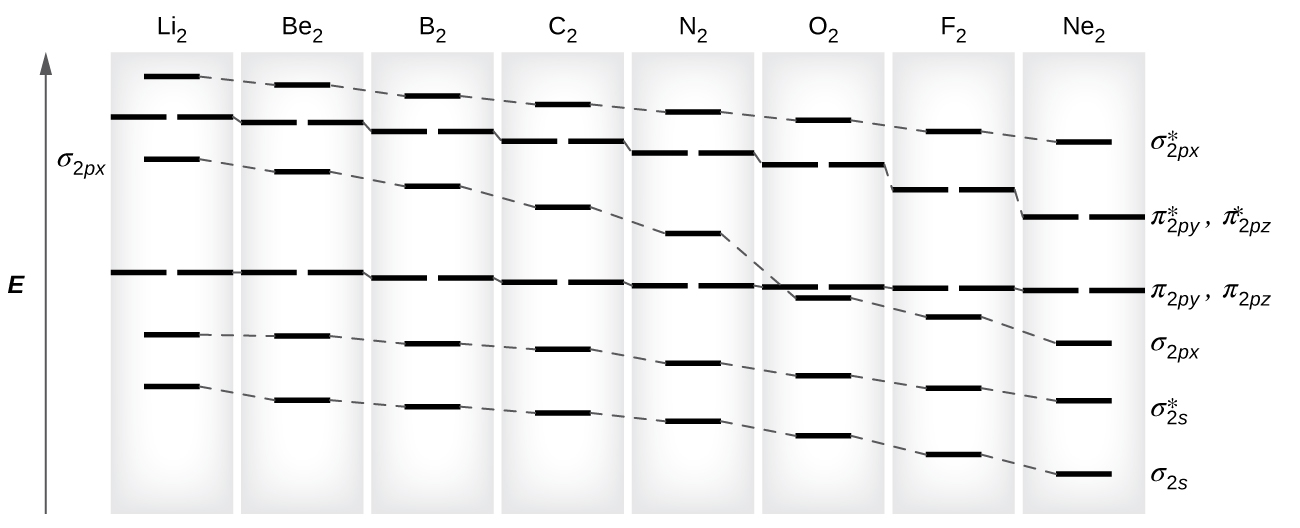
Como vimos en la teoría del enlace de valencia, los enlaces σ son generalmente más estables que los enlaces π formados a partir de orbitales atómicos degenerados. Del mismo modo, en la teoría de los orbitales moleculares, los orbitales σ suelen ser más estables que los orbitales π. Sin embargo, este no es siempre el caso. Los MO para los orbitales de valencia del segundo período se muestran en la Figura \(\PageIndex{10}\). Al observar los orbitales moleculares Ne2, vemos que el orden es consistente con el diagrama genérico que se muestra en la sección anterior. Sin embargo, para los átomos con tres o menos electrones en los orbitales p (Li a N) observamos un patrón diferente, en el que el orbital σp es más alto en energía que el conjunto πp. Obtenga el diagrama molecular orbital para un ion diatómico homonuclear sumando o restando electrones del diagrama para la molécula neutra.
Este cambio en el orden orbital ocurre debido a un fenómeno llamado la mezcla de s-p. La mezcla s-p no crea nuevos orbitales; simplemente influye las energías de los orbitales moleculares existentes. La función de la onda σs se combina matemáticamente con la función de onda σp, con el resultado de que el orbital σs se vuelve más estable y el orbital σp se vuelve menos estable (Figura \(\PageIndex{11}\)). Del mismo modo, los orbitales de antienlace también se mezclan s-p, con σs* cada vez más estable y σp* cada vez menos estable.
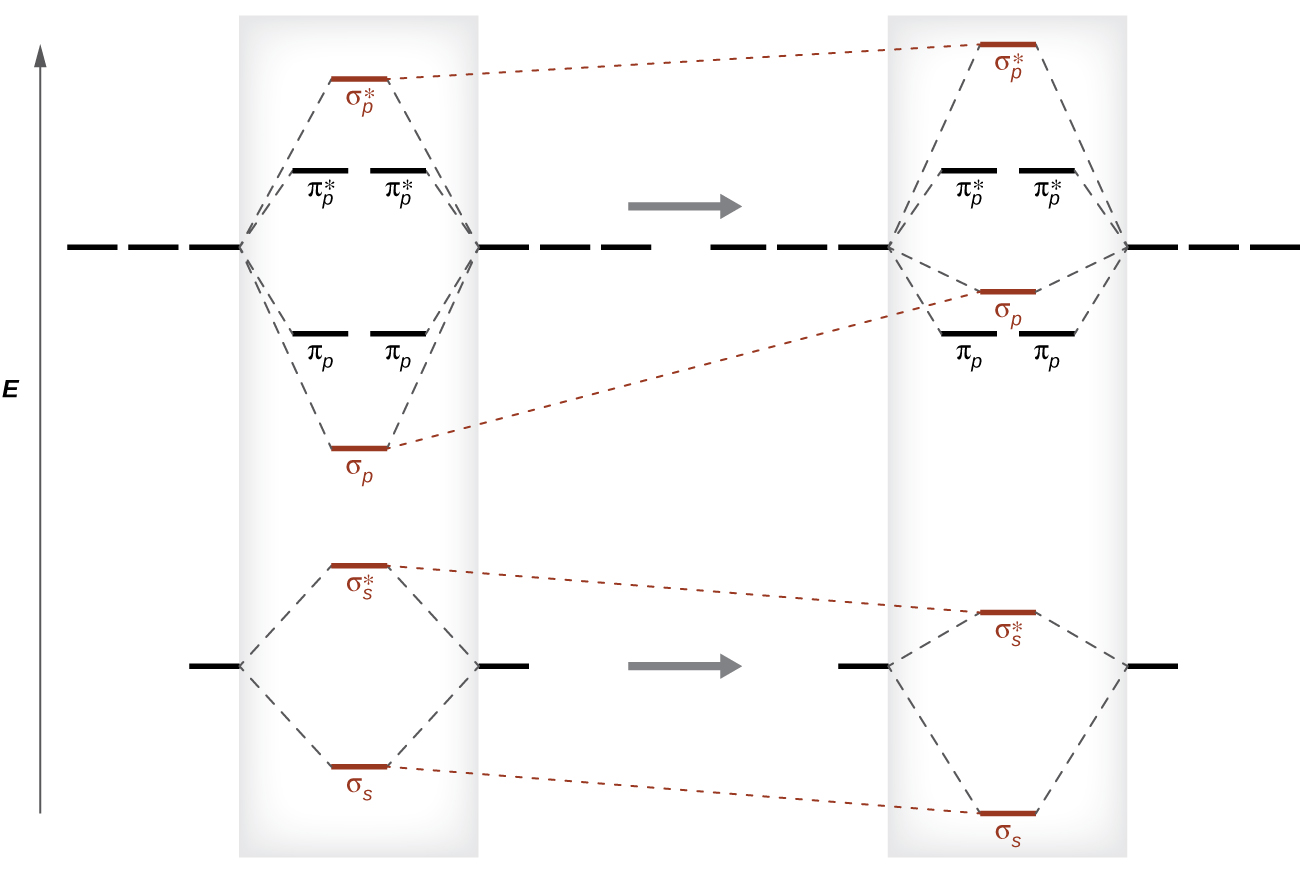
La mezcla s-p ocurre cuando los orbitales s y p tienen energías similares. La diferencia de energía entre los orbitales 2s y 2p en O, F y Ne es mayor que en Li, Be, B, C y N. Debido a esto, O2, F2 y Ne exhiben una mezcla de sp insignificante (no es suficiente para cambiar el orden de energía), y sus diagramas de MO siguen el patrón normal, como se muestra en la Figura \(\PageIndex{7}\). Todas las otras moléculas diatómicas del período 2 tienen mezcla de s-p, lo que conduce al patrón donde el orbital σp se eleva por encima del conjunto πp.
Usando los diagramas MO que se muestran en la Figura \(\PageIndex{11}\), podemos agregar electrones y determinar la configuración de electrones moleculares y el orden de enlace para cada una de las moléculas diatómicas. Como se muestra en la Tabla \(\PageIndex{1}\), las moléculas Be2 y Ne2 tendrían un orden de enlace de 0, y estas moléculas no existen.
La combinación de dos átomos de litio para formar una molécula de litio, Li2, es análoga a la formación de H2, pero los orbitales atómicos involucrados son los orbitales de valencia 2s. Cada uno de los dos átomos de litio tiene un electrón de valencia. Por lo tanto, tenemos dos electrones de valencia disponibles para el enlace orbital molecular σ2s. Debido a que ambos electrones de valencia estarían en un orbital de enlace, predeciríamos que la molécula de Li2 sería estable. De hecho, la molécula está presente en una concentración apreciable en el vapor de litio a temperaturas cercanas al punto de ebullición del elemento. También las otras moléculas con un orden de enlace mayor que cero se muestran en la Tabla \(\PageIndex{1}\).
La molécula de O2 tiene suficientes electrones para llenar la mitad del nivel \((π^∗_{2py},\:π^∗_{2pz})\). Esperamos que los dos electrones que ocupan estos dos orbitales degenerados no estén emparejados, y esta configuración electrónica molecular para O2 está de acuerdo con el hecho de que la molécula de oxígeno tiene dos electrones no emparejados (Figura \(\PageIndex{10}\)). La presencia de dos electrones no apareados ha resultado ser difícil de explicar usando las estructuras de Lewis, pero la teoría de los orbitales moleculares lo explica bastante bien. De hecho, los electrones no emparejados de la molécula del oxígeno apoyan la teoría de los orbitales moleculares.
APLICACIÓN: TEORÍA DE Enlace EN SISTEMAS EXTENDIDOS
Cuando se combinan dos orbitales atómicos idénticos en átomos diferentes, resultan dos orbitales moleculares (por ejemplo, \(H_2\) en la Figura \(\PageIndex{8}\)). El orbital de enlace es más bajo en energía que los orbitales atómicos originales porque los orbitales atómicos están en fase en el orbital molecular. El orbital de antienlace tiene mayor energía que los orbitales atómicos originales porque los orbitales atómicos están desfasados.
De manera sólida, suceden cosas similares, pero a una escala mucho más grande. Recuerde que incluso en una muestra pequeña hay una gran cantidad de átomos (típicamente> 1023 átomos) y, por lo tanto, una gran cantidad de orbitales atómicos que se pueden combinar en orbitales moleculares. Cuando se combinan los orbitales atómicos de N valencia, se combina la misma energía y cada uno con un (1) electrón, se producen orbitales de enlace N/2 (llenos) y orbitales de antienlace N/2 (vacíos). Cada orbital de enlace mostrará una disminución de energía ya que los orbitales atómicos están mayormente en fase, pero cada uno de los orbitales de enlace será un poco diferente y tendrá energías un poco diferentes. Los orbitales de antienlace mostrarán un aumento de energía ya que los orbitales atómicos están en su mayoría fuera de fase, pero cada uno de los orbitales de antienlace también será un poco diferente y tendrá energías un poco diferentes. Los niveles de energía permitidos para todos los orbitales de unión están tan juntos que forman una banda, llamada la banda de valencia. Del mismo modo, todos los orbitales de antienlace están muy juntos y forman una banda, llamada la banda de conducción. La Figura \(\PageIndex{12}\)) muestra las bandas para tres clases importantes de materiales: aislantes, semiconductores y conductores.
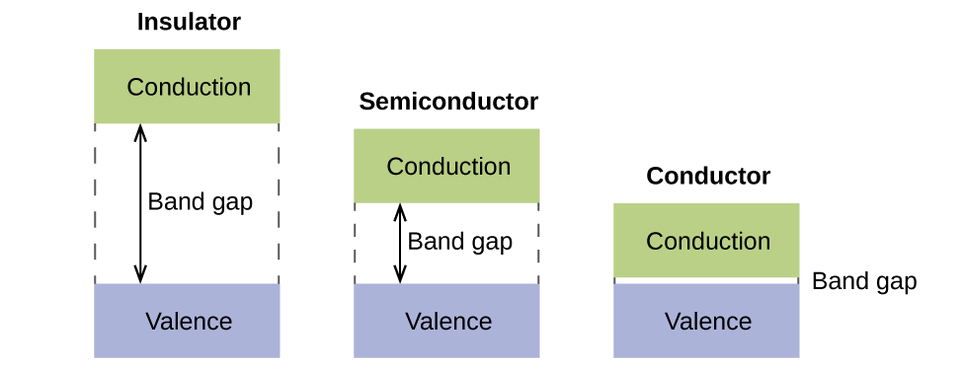
Para conducir la electricidad, los electrones se deben mover de la banda de valencia llena a la banda de conducción vacía donde pueden moverse por todo el sólido. El tamaño de la brecha de banda, o la diferencia de energía entre la parte superior de la banda de valencia y la parte inferior de la banda de conducción, determina que fácil es mover electrones entre las bandas. Solo se requiere una pequeña cantidad de energía en un conductor porque el intervalo de banda es muy pequeño. Esta pequeña diferencia de energía es "fácil" de superar, por eso son buenos conductores de electricidad. En un aislante, el espacio entre bandas es tan "grande" que muy pocos electrones se mueven hacia la banda de conducción; como resultado, los aisladores son malos conductores de la electricidad. Los semiconductores conducen la electricidad cuando se dan cantidades "moderadas" de energía para mover los electrones fuera de la banda de valencia y hacia la banda de conducción. Los semiconductores, como el silicio, se encuentran en muchos productos electrónicos.
Los semiconductores se usan en dispositivos como las computadoras, los teléfonos inteligentes y las células solares. Las células solares producen electricidad cuando la luz da la energía para mover electrones fuera de la banda de valencia. La electricidad que se genera se puede usar para alimentar una luz o herramienta, o se puede almacenar para su uso posterior cargando una batería. A partir de diciembre de 2014, hasta el 46% de la energía en la luz solar se podría convertir en electricidad mediante las células solares.
Ejemplo \(\PageIndex{2}\): LOS DIAGRAMAS ORBITALES MOLECULARES, EL ORDEN DE ENLACES Y EL NÚMERO DE ELECTRONES SIN PAR
Dibuje el diagrama orbital molecular de la molécula de oxígeno, O2. A partir de este diagrama, calcule el orden de enlace para O2. ¿Cómo explica este diagrama el paramagnetismo de O2?
Solución
Dibujamos un diagrama de energía orbital molecular similar al que se muestra en la Figura \(\PageIndex{7}\). Cada átomo de oxígeno aporta seis electrones, por lo que el diagrama aparece como se muestra en Figura \(\PageIndex{7}\).
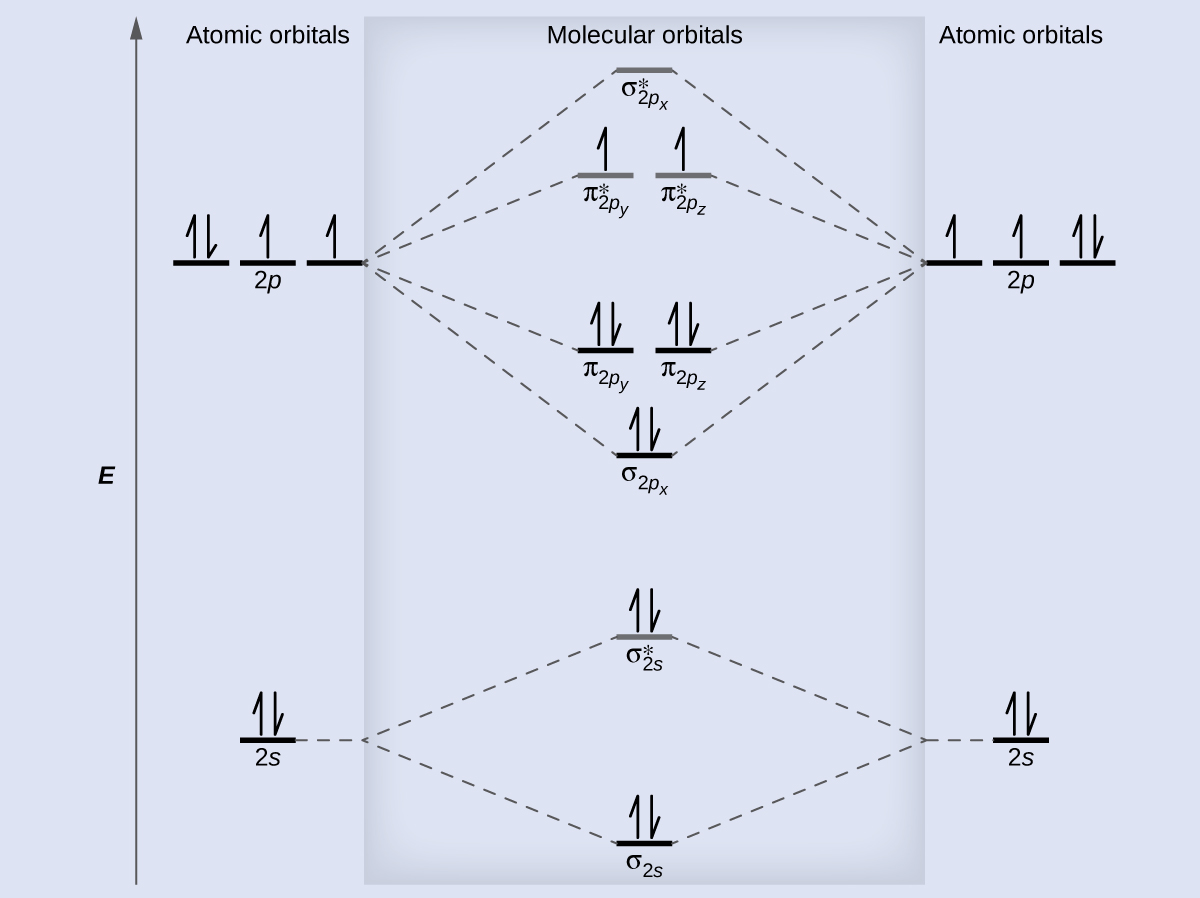
Calculamos el orden de enlace como
El paramagnetismo del oxígeno se explica por la presencia de dos electrones no apareados en los orbitales moleculares (π2py, π2pz)*.
Ejercicio \(\PageIndex{2}\)
El componente principal del aire es N2. A partir del diagrama orbital molecular de N2, prediga su orden de enlace y si es diamagnético o paramagnético.
- Respuesta
-
N2 tiene un orden de enlace de 3 y es diamagnético.
Ejemplo \(\PageIndex{3}\): PREDICCIONES DE LOS IONES CON DIAGRAMAS DE MO
Dé la configuración orbital molecular para los electrones de valencia en \(\ce{C2^2-}\). ¿Será este el ion más estable?
Solución
Mirando el diagrama MO apropiado, vemos que los orbitales π son más bajos en energía que el orbital σp. La configuración del electrón de valencia para C2 es
\((σ_{2s})^2(σ^∗_{2s})^2(π_{2py},\:π_{2pz})^4\).
Agregar dos electrones más para generar el anión \(\ce{C2^2-}\) dará una configuración electrónica de valencia de
\((σ_{2s})^2(σ^∗_{2s})^2(π_{2py},\:π_{2pz})^4(σ_{2px})^2\)
Dado que esto tiene seis electrones de enlace más que el antienlace, el orden de enlace será 3 y el ion será estable.
Ejercicio \(\PageIndex{3}\)
¿Cuántos electrones no apareados estarían presentes en un ion \(\ce{Be2^2-}\)? ¿Sería paramagnético o diamagnético?
- Respuesta
-
dos, paramagnético
Conceptos clave y resumen
La teoría del orbital molecular (MO) describe el comportamiento de los electrones en una molécula en términos de combinaciones de las funciones de la onda atómica. Los orbitales moleculares resultantes se pueden extender sobre todos los átomos en la molécula. Los orbitales moleculares de enlace se forman mediante combinaciones en fase de funciones de la onda atómica, y los electrones en estos orbitales estabilizan una molécula. Los orbitales moleculares de antienlace resultan de combinaciones desfasadas de funciones de la onda atómica y electrones en estos orbitales que hacen que una molécula sea menos estable. Los orbitales moleculares ubicados a lo largo de un eje internuclear se llaman σ MO. Se pueden formar a partir de orbitales s o a partir de orbitales p orientados de manera integral. Los orbitales moleculares formados a partir de orbitales p orientados lado a lado tienen densidad de electrones en lados opuestos del eje internuclear y se llaman los orbitales π.
Podemos describir la estructura electrónica de las moléculas diatómicas aplicando la teoría de la órbita molecular a los electrones de valencia de los átomos. Los electrones llenan los orbitales moleculares siguiendo las mismas reglas que se aplican al llenado de los orbitales atómicos; La regla de Hund y el principio de Aufbau nos dicen que los orbitales de baja energía se llenarán primero, los electrones se espaciarán antes de emparejarse, y cada orbital puede contener un máximo de dos electrones con espines opuestos. Los materiales con electrones desapareados son paramagnéticos y atraídos por un campo magnético, mientras que aquellos con electrones emparejados son diamagnéticos y repelidos por un campo magnético. La predicción correcta de las propiedades magnéticas de las moléculas es una ventaja de la teoría de los orbitales moleculares sobre las estructuras de Lewis y la teoría del enlace de valencia.
Contribuyentes
Paul Flowers (Universidad de Carolina del Norte - Pembroke), Klaus Theopold (Universidad de Delaware) y Richard Langley (Stephen F. Austin Universidad del Estado) con autores contribuyentes. Contenido del libro de texto producido por la Universidad de OpenStax tiene licencia de Atribución de Creative Commons Licencia 4.0 licencia. Descarge gratis en http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110)."
Ana Martinez (amartinez02@saintmarys.edu) contribuyó a la traducción de este texto.
C2−


