12.4: Leyes de tasas en química

habilidades para desarrollar

• Explicar la forma y función de una ley de tasas.
• Utilizar las leyes de velocidad para calcular las velocidades de reacción.
• Utilizar los datos de velocidad y concentración para identificar órdenes de reacción y derivar leyes de velocidad

Como se describe en el módulo anterior, la velocidad de una reacción se ve afectada por las concentraciones de los reactivos. Las leyes de velocidad o las ecuaciones de velocidad son expresiones matemáticas que describen la relación entre la velocidad de una reacción química y la concentración de sus reactivos. En general, una ley de tasas (o ley de tasas diferenciales, como a veces se llama) toma esta forma:

\[\ce{rate}=k[A]^m[B]^n[C]^p…\]

en el que [A], [B] y [C] representan las concentraciones molares de los reactivos, y k es el constante de velocidad, que es específico para una reacción particular a una temperatura particular. Los exponentes m, n y p suelen ser enteros positivos (aunque es posible que sean fracciones o números negativos). El constante de velocidad k y los exponentes m, n y p se deben determinar experimentalmente observando cómo cambia la velocidad de una reacción a medida que cambian las concentraciones de los reactivos. El constante de velocidad k es independiente de la concentración de A, B o C, pero varía con la temperatura y el área de la superficie.

Los exponentes en una ley de velocidad describen los efectos de las concentraciones de reactivo en la velocidad de reacción y definen el orden de reacción. Considere una reacción para la cual la ley de tasas es:

\[\ce{rate}=k[A]^m[B]^n\]

Si el exponente m es 1, la reacción es de primer orden con respecto a A. Si m es 2, la reacción es de segundo orden con respecto a A. Si n es 1, la reacción es de primer orden en B. Si n es 2, la reacción es de segundo orden en B. Si m o n es cero, la reacción es de orden cero en A o B, respectivamente, y la velocidad de la reacción no se ve afectada por la concentración de ese reactivo. El orden general de la reacción es la suma de los órdenes con respecto a cada reactivo. Si m = 1 y n = 1, el orden general de la reacción es de segundo orden (m + n = 1 + 1 = 2).

La ley de tasas:

\[\ce{rate}=k[\ce{H2O2}]\]

describe una reacción de primer orden en el peróxido de hidrógeno y de primer orden en general. La ley de tasas:

\[\ce{rate}=k[\ce{C4H6}]^2\]

describe una reacción de segundo orden en C₄H₆ y de segundo orden en general. La ley de tasas:

\[\ce{rate}=k[\ce{H+}][\ce{OH-}]\]

describe una reacción que es de primer orden en H⁺, primer orden en OH⁻ y segundo orden en general.

Ejemplo \(\PageIndex{1}\): ESCRIBIR LEYES DE TASAS DE ORDENES DE REACCIÓN

Un experimento muestra que la reacción del dióxido de nitrógeno con el monóxido de carbono:

\[\ce{NO2}(g)+\ce{CO}(g)⟶\ce{NO}(g)+\ce{CO2}(g) \nonumber\]

es de segundo orden en NO₂ y orden cero en CO a 100 °C. ¿Cuál es la ley de velocidad para la reacción?

Solución

La reacción tendrá la forma:

\[\ce{rate}=k[\ce{NO2}]^m[\ce{CO}]^n \nonumber\]

La reacción es de segundo orden en NO₂; así m = 2. La reacción es de orden cero en CO; entonces n = 0. La ley de la tasa es:

\[\ce{rate}=k[\ce{NO2}]^2[\ce{CO}]^0=k[\ce{NO2}]^2 \nonumber\]

Recuerde que un número elevado a la potencia cero es igual a 1, por lo tanto, [CO]⁰ = 1, por lo que simplemente podemos reducir la concentración de CO de la ecuación de velocidad: la velocidad de reacción depende únicamente de la concentración de NO₂ . Cuando consideremos los mecanismos de velocidad más adelante en este capítulo, explicaremos cómo la concentración de un reactivo no puede tener efecto en una reacción a pesar de estar involucrado en la reacción.

Ejercicio \(\PageIndex{1A}\)

La ley de velocidad para la reacción:

\[\ce{H2}(g)+\ce{2NO}(g)⟶\ce{N2O}(g)+\ce{H2O}(g) \nonumber\]

ha sido determinado experimentalmente como la tasa = k[NO]²[H₂]. ¿Cuáles son los órdenes con respecto a cada reactivo y cuál es el orden general de la reacción?

Respuesta:

• orden en NO = 2;
• orden en H₂ = 1;
• orden general = 3

Ejercicio \(\PageIndex{1B}\)

En una reacción de transesterificación, un triglicérido reacciona con un alcohol para formar éster y glicerol. Muchos estudiantes aprenden sobre la reacción entre el metanol (CH₃OH) y el acetato de etilo (CH₃CH₂OCOCH₃) como una reacción de muestra antes de estudiar las reacciones químicas que producen el biodiesel:

\[\ce{CH3OH + CH3CH2OCOCH3 ⟶ CH3OCOCH3 + CH3CH2OH} \nonumber\]

La ley de velocidad para la reacción entre el metanol y el acetato de etilo se determina experimentalmente bajo ciertas condiciones:

\[\ce{rate}=k[\ce{CH3OH}] \nonumber\]

¿Cuál es el orden de la reacción con respecto al metanol y el acetato de etilo, y cuál es el orden general de la reacción?

Respuesta

• orden en CH₃OH = 1;
• orden en CH₃CH₂OCOCH₃ = 0;
• orden general = 1

A veces es útil usar un método algebraico más explícito, a veces llamado el método de las tasas iniciales, para determinar los órdenes en las leyes de tasas. Para usar este método, seleccionamos dos conjuntos de datos de velocidad que difieren en la concentración de un solo reactivo y establecemos una relación de las dos velocidades y las dos leyes de velocidad. Después de cancelar términos que son iguales, nos queda una ecuación que contiene solo uno desconocido, el coeficiente de concentración que varía. Luego resolvemos esta ecuación para el coeficiente.

Ejemplo \(\PageIndex{2}\): DETERMINANDO UNA LEY DE TASAS USANDO LAS TASAS INICIALES

El ozono en la atmósfera superior se agota cuando reacciona con los óxidos de nitrógeno. Las tasas de las reacciones de los óxidos de nitrógeno con el ozono son factores importantes para decidir la importancia de estas reacciones en la formación del agujero del ozono sobre la Antártida (Figura \(\PageIndex{1}\)). Una de esas reacciones es la combinación del óxido nítrico, NO, con el ozono, O₃:

Figura\(\PageIndex{1}\): En los últimos años, la concentración del ozono atmosférico sobre la Antártida ha disminuido durante el invierno. Este mapa muestra la disminución de la concentración como un área púrpura. (crédito: modificación del trabajo de la NASA)

\[\ce{NO}(g)+\ce{O3}(g)⟶\ce{NO2}(g)+\ce{O2}(g)\nonumber\]

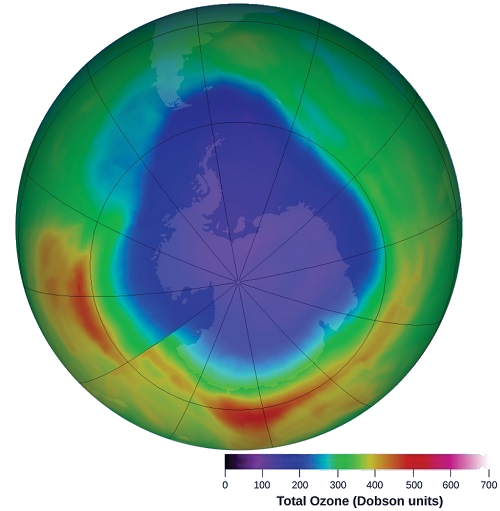
Esta reacción ha sido estudiada en el laboratorio, y los siguientes datos de velocidad se determinaron a 25 ° C.

Prueba	\([\ce{NO}]\) (mol/L)	\([\ce{O3}]\) (mol/L)	\(\dfrac{Δ[\ce{NO2}]}{Δt}\:\mathrm{(mol\:L^{−1}\:s^{−1})}\)
1	1.00 × 10^−6	3.00 × 10^−6	6.60 × 10^−5
2	1.00 × 10^−6	6.00 × 10^−6	1.32 × 10^−4
3	1.00 × 10^−6	9.00 × 10^−6	1.98 × 10^−4
4	2.00 × 10^−6	9.00 × 10^−6	3.96 × 10^−4
5	3.00 × 10^−6	9.00 × 10^−6	5.94 × 10^−4

Determine la ley de velocidad y el constante de velocidad para la reacción a 25 ° C.

Solución

La ley de velocidad tendrá la forma:

\[\ce{rate}=k[\ce{NO}]^m[\ce{O3}]^n\]

Podemos determinar los valores de m, n y k a partir de los datos experimentales usando el siguiente proceso de tres partes:

1. Determine el valor de m a partir de los datos en los que [NO] varía y [O₃] es constante. En los últimos tres experimentos, [NO] varía mientras que [O₃] permanece constante. Cuando [NO] se duplica de la prueba 3 a 4, la tasa se duplica, y cuando [NO] se triplica de la prueba 3 a 5, la tasa también se triplica. Por lo tanto, la tasa también es directamente proporcional a [NO], y m en la ley de tasa es igual a 1.
2. Determine el valor de n a partir de los datos en los que [O₃] varía y [NO] es constante. En los primeros tres experimentos, [NO] es constante y [O₃] varía. La velocidad de la reacción cambia en proporción directa al cambio en [O₃]. Cuando [O3] se duplica de la prueba 1 a 2, la tasa se duplica; cuando [O₃] se triplica de la prueba 1 a la 3, la tasa aumenta también se triplica. Por lo tanto, la tasa es directamente proporcional a [O₃], y n es igual a 1. La ley de tasa es así:
   \[\ce{rate}=k[\ce{NO}]^1[\ce{O3}]^1=k[\ce{NO}][\ce{O3}]\]
3. Determine el valor de k de un conjunto de concentraciones y la tasa correspondiente.
   \[\begin{align*}
   k&=\mathrm{\dfrac{rate}{[NO][O_3]}}\\
   &=\mathrm{\dfrac{6.60×10^{−5}\cancel{mol\: L^{−1}}\:s^{−1}}{(1.00×10^{−6}\cancel{mol\: L^{−1}})(3.00×10^{−6}\:mol\:L^{−1})}}\\
   &=\mathrm{2.20×10^7\:L\:mol^{−1}\:s^{−1}}
   \end{align*}\]

   El gran valor de k nos dice que esta es una reacción rápida que podría desempeñar un papel importante en el agotamiento del ozono si la concentración de NO es lo suficientemente grande.

Ejercicio \(\PageIndex{2}\)

El acetaldehído se descompone cuando se calienta para producir el metano y el monóxido de carbono de acuerdo con la ecuación

\[\ce{CH3CHO}(g)⟶\ce{CH4}(g)+\ce{CO}(g)\]

Determine la ley de velocidad y el constante de velocidad para la reacción a partir de los siguientes datos experimentales:

Prueba	\([\ce{CH3CHO}]\) (mol/L)	\(−\dfrac{Δ[\ce{CH3CHO}]}{Δt}\mathrm{(mol\:L^{−1}\:s^{−1})}\)
1	1.75 × 10^−3	2.06 × 10^−11
2	3.50 × 10^−3	8.24 × 10^−11
3	7.00 × 10^−3	3.30 × 10^−10

Respuesta

\(\ce{rate}=k[\ce{CH3CHO}]^2\) con k = 6.73 × 10⁻⁶ L/mol/s

Ejemplo \(\PageIndex{3}\): Determinando las leyes de velocidad usando las tasa de reacción iniciales

Usando el método de tasas iniciales y los datos experimentales, determine la ley de tasas y el valor del constante de tasas para esta reacción:

\[\ce{2NO}(g)+\ce{Cl2}(g)⟶\ce{2NOCl}(g)\]

Prueba	[NO] (mol/L)	\([Cl_2]\) (mol/L)	\(−\dfrac{Δ[\ce{NO}]}{Δt}\mathrm{(mol\:L^{−1}\:s^{−1})}\)
1	0.10	0.10	0.00300
2	0.10	0.15	0.00450
3	0.15	0.10	0.00675

Solución

La ley de velocidad para esta reacción tendrá la forma:

\[\ce{rate}=k[\ce{NO}]^m[\ce{Cl2}]^n\]

Como en el Ejemplo \(\PageIndex{2}\), podemos abordar este problema de forma gradual, determinando los valores de m y n a partir de los datos experimentales y luego usando estos valores para determinar el valor de k. En este ejemplo, sin embargo, utilizaremos un enfoque diferente para determinar los valores de m y n:

Determine el valor de m a partir de los datos en los que [NO] varía y [Cl₂] es constante. Podemos escribir las proporciones con los subíndices x e y para indicar datos de dos ensayos diferentes:

\[\dfrac{\ce{rate}_x}{\ce{rate}_y}=\dfrac{k[\ce{NO}]^m_x[\ce{Cl2}]^n_x}{k[\ce{NO}]^m_y[\ce{Cl2}]^n_y}\]

El uso de la tercera prueba y la primera prueba, en la que [Cl₂] no varía, proporciona:

\[\mathrm{\dfrac{rate\: 3}{rate\: 1}}=\dfrac{0.00675}{0.00300}=\dfrac{k(0.15)^m(0.10)^n}{k(0.10)^m(0.10)^n}\]

Después de cancelar términos equivalentes en el numerador y el denominador, nos quedamos con:

\[\dfrac{0.00675}{0.00300}=\dfrac{(0.15)^m}{(0.10)^m}\]

que se simplifica a:

\[2.25=(1.5)^m\]

Podemos usar logaritmos naturales para determinar el valor del exponente m:

\(\begin{align*}
\ln(2.25)&=m\ln(1.5)
\dfrac{\ln(2.25)}{\ln(1.5)}&=m
2&=m
\end{align*}\)

Podemos confirmar el resultado fácilmente, ya que:

\(1.5^2=2.25\)

• Determine el valor de n a partir de datos en los que [Cl₂] varía y [NO] es constante. \[\mathrm{\dfrac{rate\: 2}{rate\: 1}}=\dfrac{0.00450}{0.00300}=\dfrac{k(0.10)^m(0.15)^n}{k(0.10)^m(0.10)^n}\]

  La cancelación da:

  \[\dfrac{0.0045}{0.0030}=\dfrac{(0.15)^n}{(0.10)^n}\]

  que se simplifica a:

  \[1.5=(1.5)^n\]

  Por lo tanto, n debe ser 1, y la forma de la ley de tasas es:

  \[\ce{Rate}=k[\ce{NO}]^m[\ce{Cl2}]^n=k[\ce{NO}]^2[\ce{Cl2}]\]
• Determine el valor numérico del constante de velocidad k con las unidades apropiadas. Las unidades para la velocidad de una reacción son mol/L/s. Las unidades para k son lo que sea necesario para que la sustitución en la expresión de la ley de velocidad proporcione las unidades apropiadas para la velocidad. En este ejemplo, las unidades de concentración son mol³/L³. Las unidades para k deben ser mol − 2 L²/s, de modo que la tasa esté en términos de mol/L/s.

  Para determinar el valor de k una vez que se ha resuelto la expresión de la ley de velocidad, simplemente conecte los valores de la primera prueba experimental y resuelve para k:

  \(\begin{align*}
  \mathrm{0.00300\:mol\:L^{−1}\:s^{−1}}&=k\mathrm{(0.10\:mol\:L^{−1})^2(0.10\:mol\:L^{−1})^1}\\
  k&=\mathrm{3.0\:mol^{−2}\:L^2\:s^{−1}}
  \end{align*}\)

Ejercicio \(\PageIndex{3}\)

Use los datos de velocidad inicial dados para derivar la ley de velocidad para la reacción cuya ecuación es:

\[\ce{OCl-}(aq)+\ce{I-}(aq)⟶\ce{OI-}(aq)+\ce{Cl-}(aq)\]

Prueba	[OCl^−] (mol/L)	[I^−] (mol/L)	Tasa Inicial (mol/L/s)
1	0.0040	0.0020	0.00184
2	0.0020	0.0040	0.00092
3	0.0020	0.0020	0.00046

Determine la expresión de la ley de velocidad y el valor del constante de velocidad k con unidades apropiadas para esta reacción.

Respuesta

\(\mathrm{\dfrac{rate\: 2}{rate\: 3}}=\dfrac{0.00092}{0.00046}=\dfrac{k(0.0020)^x(0.0040)^y}{k(0.0020)^x(0.0020)^y}\)

2.00 = 2.00^y

y = 1

\(\mathrm{\dfrac{rate\: 1}{rate\: 2}}=\dfrac{0.00184}{0.00092}=\dfrac{k(0.0040)^x(0.0020)^y}{k(0.0020)^x(0.0040)^y}\)

\(\begin{align*}
2.00&=\dfrac{2^x}{2^y}\\
2.00&=\dfrac{2^x}{2^1}\\
4.00&=2^x\\
x&=2
\end{align*}\)

Sustituyendo los datos de la concentración de la primer prueba y resolviendo para los rendimientos de k nos da:

\(\begin{align*}
\ce{rate}&=k[\ce{OCl-}]^2[\ce{I-}]^1\\
0.00184&=k(0.0040)^2(0.0020)^1\\
k&=\mathrm{5.75×10^4\:mol^{−2}\:L^2\:s^{−1}}
\end{align*}\)

La orden de reacción y la tasa de unidades constantes

En algunos de nuestros ejemplos, los órdenes de reacción en la ley de velocidad resultan ser los mismos que los coeficientes en la ecuación química para la reacción. Esto es simplemente una coincidencia y no es siempre el caso. Las leyes de velocidad pueden exhibir órdenes fraccionales para algunos reactivos, y algunas veces se observan órdenes de reacción negativas cuando un aumento en la concentración de un reactivo causa una disminución en la velocidad de la reacción. Se proporcionan algunos ejemplos que ilustran estos puntos:

\(\ce{NO2 + CO⟶NO + CO2}\hspace{20px}\ce{rate}=k[\ce{NO2}]^2\\
\ce{CH3CHO⟶CH4 + CO}\hspace{20px}\ce{rate}=k[\ce{CH3CHO}]^2\\
\ce{2N2O5⟶2NO2 + O2}\hspace{20px}\ce{rate}=k[\ce{N2O5}]\\
\ce{2NO2 + F2⟶2NO2F}\hspace{20px}\ce{rate}=k[\ce{NO2}][\ce{F2}]\\
\ce{2NO2Cl⟶2NO2 + Cl2}\hspace{20px}\ce{rate}=k[\ce{NO2Cl}]\)

Es importante tener en cuenta que las leyes de velocidad se determinan solo por experimento y no se predicen de manera confiable por la estequiometría de la reacción.

Las órdenes de reacción también juegan un papel en la determinación de las unidades para el constante de velocidad k. En el Ejemplo \(\PageIndex{2}\), una reacción de segundo orden, encontramos que las unidades para k son \(\mathrm{L\:mol^{- 1}\:s^{-1}}\), mientras que en el Ejemplo \(\PageIndex{3}\), una reacción de tercer orden, encontramos que las unidades para k son mol − 2 L²/s. En términos más generales, las unidades para el constante de velocidad para una reacción de orden \((m+n)\) son \(\ce{mol}^{1−(m+n)}\ce L^{(m+n)−1}\ce s^{−1}\). La tabla \(\PageIndex{1}\) resume las unidades de la velocidad constante para órdenes de reacción comunes.

Tabla \(\PageIndex{1}\): Tasas constantes para las órdenes de reacción comunes

Orden de Reacción	Unidades de k
\( (m+n)\)	\(\ce{mol}^{1−(m+n)}\ce L^{(m+n)−1}\ce s^{−1}\)
cero	mol/L/s
primero	s^−1
segundo	L/mol/s
tercero	mol^−2 L^2 s^−1

Tenga en cuenta que las unidades en la tabla también se pueden expresar en términos de molaridad (M) en lugar de mol/L. Además, se pueden usar unidades de tiempo que no sean el segundo (como minutos, horas, días), según la situación.

Resumen

Las leyes de velocidad afectadas una descripción matemática de cómo los cambios en la cantidad de una sustancia afectada la velocidad de una reacción química. Las leyes de velocidad se determinan experimentalmente y no se pueden predecir por la estequiometría de la reacción. El orden de la reacción describe cuánto afecta un cambio en la cantidad de cada sustancia a la velocidad general, y el orden general de una reacción es la suma de los órdenes de cada sustancia presente en la reacción. Las órdenes de reacción son los comandos de primer orden, segundo orden u orden cero, pero son posibles los pedidos fraccionarios e incluso negativos.

Glosario

método de tasas iniciales

uso de un método algebraico más explícito para determinar los órdenes en una ley de tasas

orden de reacción general

suma de las órdenes de reacción para cada sustancia representada en la ley de velocidad

tasa constante (k)

proporcionalidad constante en la relación entre la velocidad de reacción y las concentraciones de reactivos

ley de tasas

(también, ecuación de velocidad) ecuación matemática que muestra la dependencia de la velocidad de reacción de la constante de velocidad y la concentración de uno o más reactivos

orden de reacción

valor de un exponente en una ley de tasa, expresado como un número ordinal (por ejemplo, orden cero para 0, primer orden para 1, segundo orden para 2, etc.)

Contribuyentes

• Paul Flowers (Universidad de Carolina del Norte - Pembroke), Klaus Theopold (Universidad de Delaware) y Richard Langley (Stephen F. Austin Universidad del Estado) con autores contribuyentes. Contenido del libro de texto producido por la Universidad de OpenStax tiene licencia de Atribución de Creative Commons Licencia 4.0 licencia. Descarge gratis en http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110)."

• Ana Martinez ([e-mail]) contribuyó a la traducción de este texto.