3.7: Actividad Óptica
- Page ID
- 2329
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Mientras su nariz, con la ayuda de sus proteínas receptoras quirales, puede diferenciar entre (R)-carvone y (S)-carvone, le seria difícil a alguien con gripe distinguir entre los dos enantiómeros usando la mojaría de técnicas orgánicas estándares de laboratorio. Enantiómeros tienen cualidades físicas idénticas: la misma temperatura de derretir, hervir, comportamiento de solubilidad, movilidad cromatográfica, índice de refractividad, etc. Sin la ayuda de un agente quiral (ej. las proteínas receptoras de olores) una de las únicas maneras en la cual un par de enantiómeros pueden ser distinguidos en un laboratorio es por medio de un método conocido como polarimetría.
Usted tal vez sabrá atreves de el estudio de física que la luz es caracterizada por electricidad y campos magnéticos que fluctúa en las superficies que son perpendiculares. En “luz normal”, sin polarizar, estas fluctuaciones son orientadas de manera descontrolada en la superficies. Luz que ha pasado por un filtro polarizador fluctúa en una sola dirección, y es llamada plano de luz polarizada.
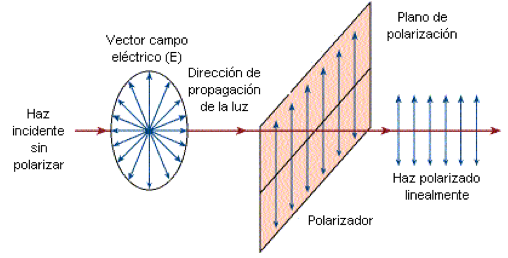
Moleculas quilares tienen propiedades conosidas como actividad optica: esto significa que un rayo de luz, al momento que pasa atravez de la sustancia quiral, interactuara con la sustancia de una manera que el angulo del plano de fluctuacion rotara.
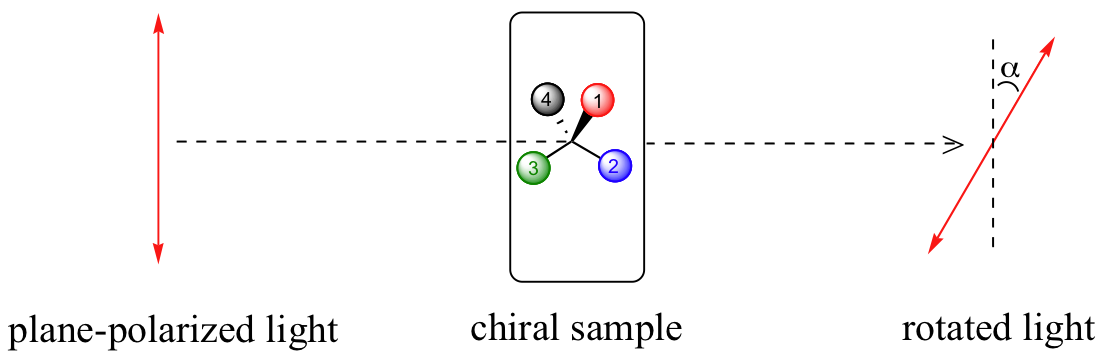
Enantiómeros en su forma pura siempre rotaran el plano-polarizado de luz igualmente, pero en direcciones diferente. Si una muestra estereoquímica pura de (S)-carvone, por ejemplo, rota el plano-polarizado de luz +10˚(de la misma manera de las ajugas del reloj), entonces una muestra de (R)-carvone (en la misma concentración y bajo las mismas condiciones experimentales) rotara la luz -10˚ (en contra de las ajugas del reloj).
La magnitud observada de la actividad óptica depende de temperatura, longitud de onda, solvente, concentración de la muestra quiral, y la longitud de el tubo de muestra. (La longitud es la longitud, expresada en decímetros (1dm – 10cm), que el plano-polarizado de luz viaja atreves de la muestra quiral). Típicamente, actividad óptica es medida en tubos de 1 decámetro (10cm) a una temperatura de 25 ˚C, usando una fuente de luz llamada “linea-D” que viene de una lámpara de sodio, con una longitud de onda de 589 y es color amarillo. La rotación especifica de una muestra a 25˚ es expresado por la ecuación:
\[ [\alpha]_D^{25} = \dfrac{\alpha}{lc}\]
Donde α es la rotación observada, l es la longitud en dm (decímetros, o 10 cm) y c es la concentración de la muestra en gramos por 100 mL. Debido a que cada molécula quiral tiene una rotación especifica, medidas de polimetría pueden ser usadas para determinar la concentración de una muestra pura de una solución quiral, asumiendo que la rotación especifica ya es conocida. Este es un método común para determinar la concentración de soluciones azucaradas.
Debido a que los enantiómeros R y S tienen la misma, pero opuestas actividad de rotación óptica, naturalmente sigue que una mezcla racémica conteniendo 50:50 de dos enantiómeros no tendrá actividad óptica observada. Pero, si sabemos la rotación especifica de una molécula, podemos calcular fácilmente la proporción de enantiómeros presentes en una mezcla de dos enantiómeros basados en la actividad óptica medida. Cuando una mezcla contiene mas de un enantiómero que del otro, químicos seguido usan el concepto llamado exceso enantiómerico (ee) para cuantificar la diferencia. Exceso enantiómerico puede ser expresado como:
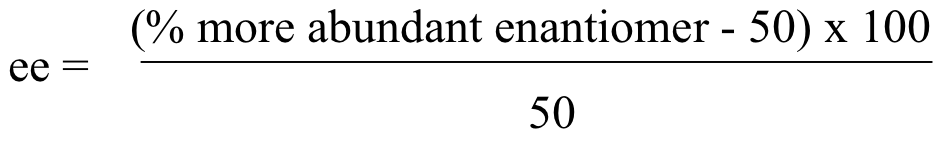
Por ejemplo, una mezcla que contiene 60% R enantiómero (y 40% S enantiomero) tiene 20% exceso del enantiómero R: ((60-50) x 100) / 50 = 20 %.
Expresado en términos de rotación óptica (usando valores absolutos):

Ejemplo 3.9
Moléculas quirales frecuentemente son clasificadas acorde a su rotación especifica, como en (S)-(+)-carvone y (R)-(-)-carvone, o (±)-carvone para la mezcla racémica. De cualquier manera, no hay conexión entre la designación de R/S y el signo especifico de rotación. Sin hacer el experimento polimétrico o buscar en literatura, no sabríamos si (-)-carvone tiene configuración R y (+)-carvone tiene una configuración S.


