4.1: Introducción a la espectrometría de masas
- Page ID
- 2336
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)4.1A: El espectro electromagnético
Radiación electromagnética, como podrán recordar de una clase de química o física anterior, se compone de ondas eléctricas y magnéticas que oscilan en planos perpendiculares. La luz visible es la radiación electromagnética . También lo son los rayos gamma que son emitidos por el combustible nuclear gastado, las radiografías que un médico utiliza para visualizar los huesos, la luz ultravioleta que causa una quemadura dolorosa cuando se le olvida aplicar protector solar, la luz infrarroja que el ejército utiliza en gafas de visión nocturna, las microondas que usted utiliza para calentar sus burritos congelados, y las ondas de radiofrecuencia que llevan la música a cualquier persona que está lo suficiente pasado de moda como para seguir escuchando la radio FM o AM.
Así como las olas del mar, ondas electromagnéticas viajan en una dirección definida. Mientras que la velocidad de las olas del mar puede variar, sin embargo, la velocidad de las ondas electromagnéticas - comúnmente referido como la velocidad de la luz - es esencialmente una constante, aproximadamente 300 millones de metros por segundo. Esto es cierto si estamos hablando de la radiación gamma o luz visible. Obviamente, hay una gran diferencia entre estos dos tipos de ondas - estamos rodeados por este último durante más de la mitad de nuestro tiempo en la tierra, mientras que esperamos nunca ser expuestos a la radiación gamma en un grado significativo. Las diferentes propiedades de los diversos tipos de radiación electromagnética se deben a diferencias en sus longitudes de onda, y las diferencias correspondientes en sus energías: longitudes de onda más cortas corresponden a una energía más alta.
La radiación de alta energía (tales como gamma y rayos X) está compuesto de ondas muy cortas - tan corto como 10-16 metros de cresta a cresta. Olas más largas son mucho menos enérgicas, y por lo tanto son menos peligrosas para los seres vivos. Ondas de luz visibles están en el rango de 400 - 700 nm (nanómetros, o 10-9 m), mientras que las ondas de radio pueden ser de varios cientos de metros de longitud.
La noción de que la radiación electromagnética contiene una cantidad cuantificable de energía quizás puede entenderse mejor si hablamos de la luz como una corriente de partículas, llamadas fotones, en vez de como una onda. (Recordemos el concepto conocido como 'dualidad onda-partícula ': al nivel cuántico, el comportamiento de las ondas y el de las partículas se vuelven indistinguibles, y las partículas muy pequeñas tienen una 'longitud de onda' observable). Si describimos la luz como una corriente de fotones, la energía de una longitud de onda particular se puede expresar como:
\[E = \dfrac{hc}{\lambda} \tag{4.1.1}\]
donde
- \(E\) es energía en kcal/mol,
- \(\lambda\) (la letra Griega lambda) es la longitud de onda en metros,
- \(c\) es 3.00 x 108 m/s (la velocidad de la luz), y
- \(h\) es 9.537 x 10-14 kcal•s•mol-1, un número conocido como el constante de Planck.
Debido a que la radiación electromagnética viaja a una velocidad constante, cada longitud de onda corresponde a una frecuencia dada, que es el número de veces por segundo que una cresta pasa por un punto dado. Las ondas más largas tienen frecuencias más bajas, y ondas más cortas tienen frecuencias más altas. La frecuencia se informa comúnmente en hertz (Hz), que significa 'ciclos por segundo', o 'ondas por segundo'. La unidad estándar para la frecuencia es s-1.
Cuando se habla de las ondas electromagnéticas, podemos referirnos tanto a la longitud de onda o a la frequencia - los dos valores se pueden interconvertir utilizando la simple expresión:
λν = c
donde ν (la letra Griega 'nu') es la frecuencia en s-1. La luz roja visible con una longitud de onda de 700 nm, por ejemplo, tiene una frecuencia de 4.29 x 1014 Hz, y una energía de 40.9 kcal por mol de fotones.
El rango completo de longitudes de onda de radiación electromagnética se conoce como el espectro electromagnético.
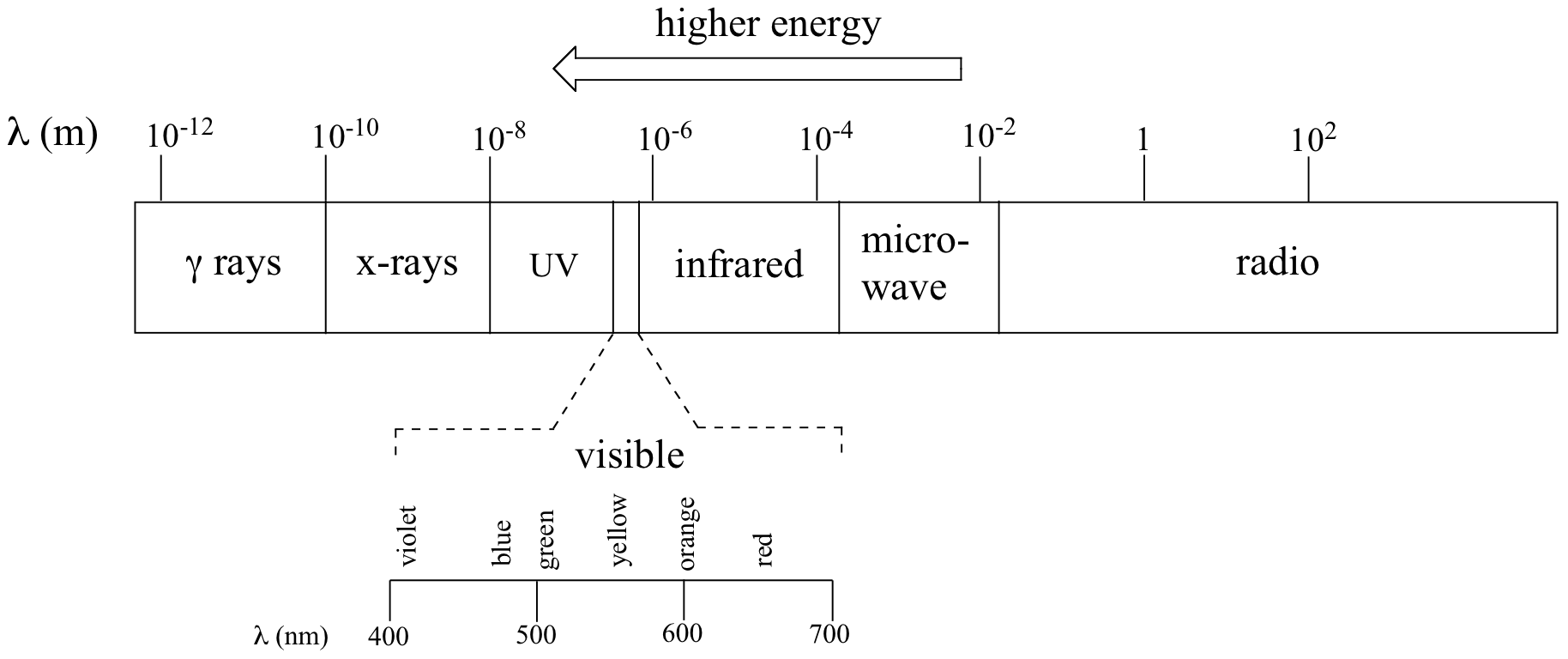
Observe en la figura anterior que la luz visible ocupa sólo una banda angosta del espectro completo. La luz blanca del sol o una bombilla de luz es una mezcla de todas las longitudes de onda visibles. Usted ve la región visible del espectro electromagnético dividido en sus diferentes longitudes de onda cada vez que ves un arco iris: luz violeta tiene la longitud de onda más corta, y la luz roja tiene la más larga.
Ejercicio 4.1.1
La luz visible tiene una longitud de onda de alrededor de 400 a 700 nm. ¿Cuál es el rango de frecuencia correspondiente? ¿Cuál es el rango de energía correspondiente, en kcal/mol de fotones?
4.1B: Espectroscopia molecular – la idea básica
En un experimento de espectroscopía, se permite la radiación electromagnética de un rango especificado de longitudes de onda para pasar a través de una muestra que contiene un compuesto de interés. Las moléculas de la muestra absorben la energía de algunas de las longitudes de onda, y como resultado saltan de una energía baja 'estado fundamental' hacia una energía más alta 'estado excitado'. Otras longitudes de onda no son absorbidas por la molécula de la muestra, entonces se van de paso. Un detector en el otro lado de la muestra registra cuales ondas de longitude fueron absorbidos, y en qué medida fueron absorbidos.
Aquí está la clave para la espectroscopia molecular: una molécula dada absorberá específicamente sólo aquellas longitudes de onda que tienen energías que corresponden a la diferencia de energía de la transición que está ocurriendo. Por lo tanto, si la transición involucra a la molécula saltando desde el estado fundamental A al estado excitado B, con una diferencia de energía de ΔE, la molécula absorberá la radiación con longitud de onda específica que corresponde a ΔE, mientras que permite que otras longitudes de onda pasen a través de sin absorber.
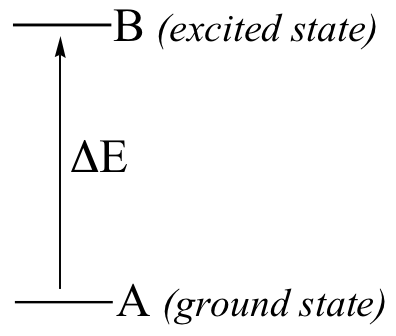
Con observar cuales longitudes de onda absorbe una molécula, y en qué medida les absorbe, podemos obtener información sobre la naturaleza de las transiciones energéticas que una molécula es capaz de someterse a, y de este modo información sobre su estructura.
Estas ideas generalizadas pueden sonar todas bastante confusas en este punto, pero las cosas se harán mucho más claras al comenzar a discutir ejemplos específicos.


