15.2: Adición electrofílica

Solutions to exercises

15.2A: Electrophilic addition reactions - the general picture

In electrophilic reactions, pi-bonded electrons act as bases and nucleophiles. It is relatively simple to understand how the lone pair of electrons on a thiol group could be nucleophilic - they are free and unbonded, a clear case of electron richness.  In the same sense, it is easy to see how an electron-rich enolate carbon is nucleophilic in the context of aldol and Claisen condensation reactions.  But the pi bonds of alkenes?  These electrons are not free, they are already involved in a bond! 

The key to understanding electrophilic reactions is to consider again the geometry of alkene groups and the orbitals that overlap to form the pi bond. Recall (section 1.5C) that the two carbons in an alkene group are both sp² hybridized, meaning that each carbon has three sp² hybrid orbitals extending out in the same plane, and a single, unhybridized p orbital perpendicular to that plane - one lobe above the plane, one lobe below. 

The unhybridized p orbitals on the two alkene carbons overlap, in a side-by-side fashion, to form the pi bond, which protrudes above and below the plane formed by the sigma bonds.  The two electrons shared in this pi bond are, on average, further away from the carbon nuclei than the sigma-bonded electrons, and thus are held less tightly.  This in turn means that less energy is required to pull the pi-bonded electrons out of their orbital - they are, in other words, more reactive.  Now, imagine that an electrophile approaches an alkene. The electrophile, because it is electron-poor,  may be able to pull the pi-bonded alkene electrons out of their bond and into one of its empty orbitals.

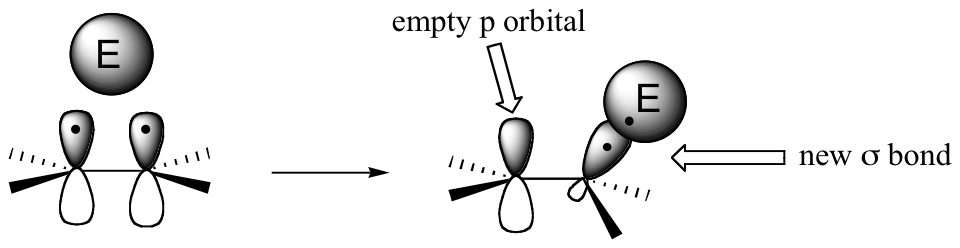
If this happens, a new sigma bond is formed between one of the carbons and the electrophile (and the carbon, which was sp²-hybridized when it was part of the alkene, is now sp³-hybridized).  The other alkene carbon, which lost the pi electrons, is still sp²-hybridized, but it now bears a positive charge because its unhybridized 2p_z orbital is empty.  But it won't stay empty for long - a carbocation is generally a very reactive, unstable intermediate.  In an electrophilic addition reaction, a nearby nucleophile (often water) will quickly donate a pair of electrons to form a new sbond, and with four sigma bonds the carbon will change to sp³ hybridization. 

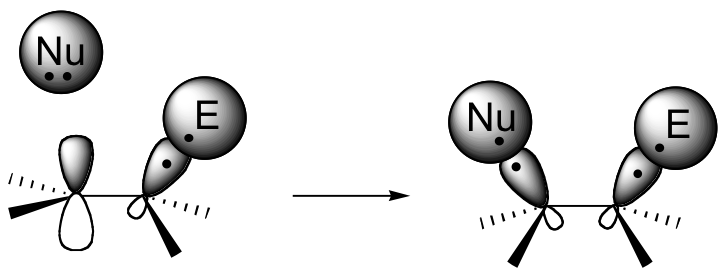
The first step in an electrophilic addition, in which the pi electrons in an alkene break away to attack an electrophile, is slower than the second step, in which a nucleophile attacks the positively charged intermediate. 

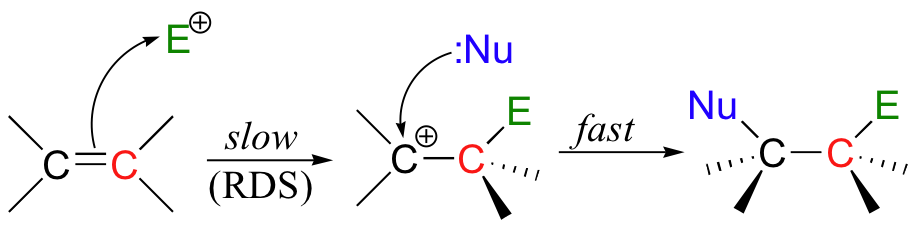
In other words, the first step is the rate-determining step (RDS).

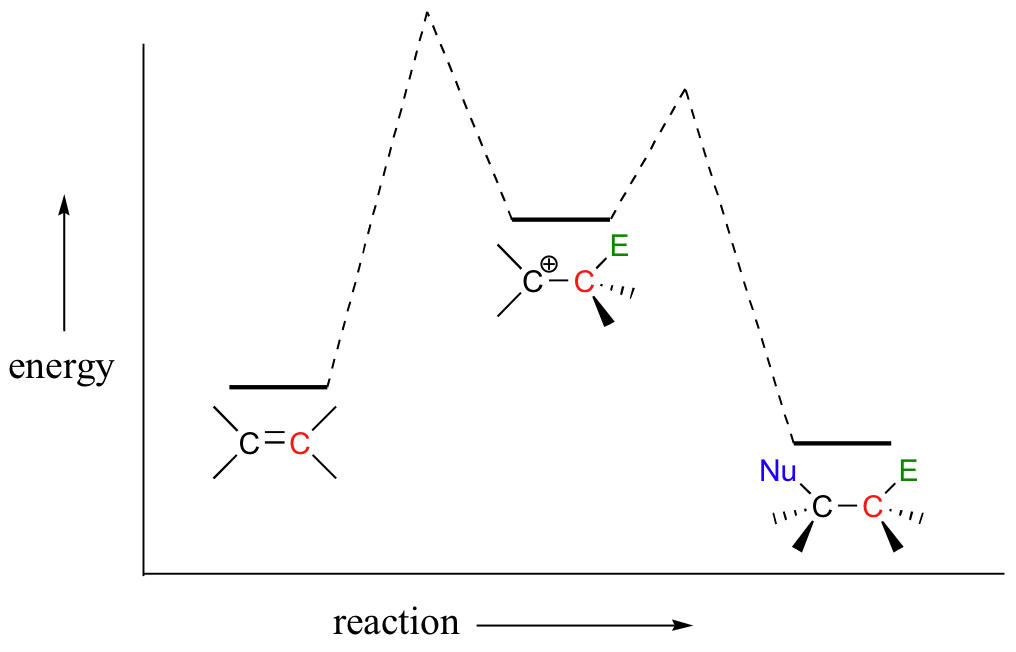
This makes sense, because the first step involves breaking an existing bond and forming a high energy carbocation intermediate (this process has a high energy barrier), whereas the second step involves quenching that intermediate and forming a new bond (this process has a very low energy barrier).

Template:ExampleStart

 

Exercise 15.1: Draw the two transition states of the generalized electrophilic addition reaction shown above.

 

Template:ExampleEnd

 

15.2B: The regiochemistry of electrophilic addition

A very important point to notice in the electrophilic addition reaction above is that, if the starting alkene is asymmetrical, there are two possible courses that could be followed, depending on which of the two alkene carbons forms the new sigma bond in the first step. 

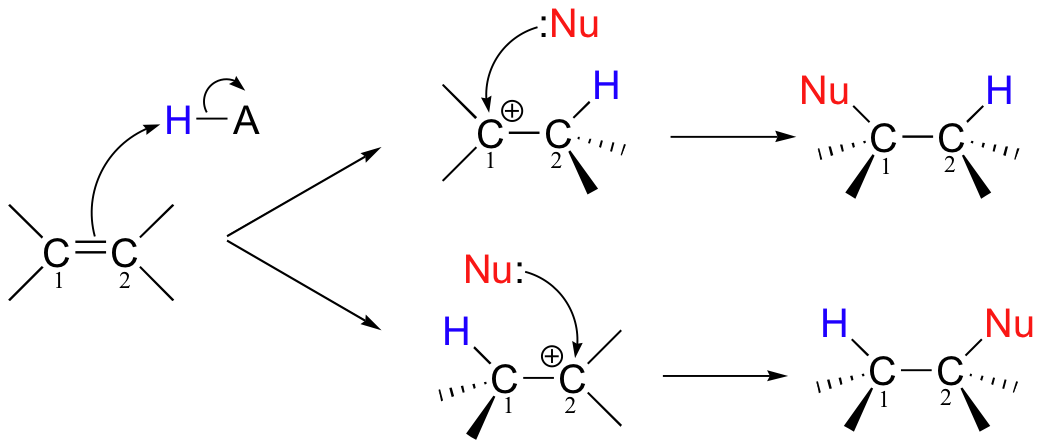
Of course, the two reaction courses involve two different carbocation intermediates, which may have different energy levels.  Two different products are possible, and in general the product which predominates will be the one that is derived from the lower-energy carbocation intermediate. 

This important regiochemical principle is nicely illustrated by a simple electrophilic addition that is commonly carried out in the organic laboratory: the conversion of an alkene to an alkyl bromide by electrophilic addition of HBr to the double bond.   Let's look at a hypothetical addition of HBr to 2-methyl-2-butene, pictured below.  Two different regiochemical outcomes are possible:

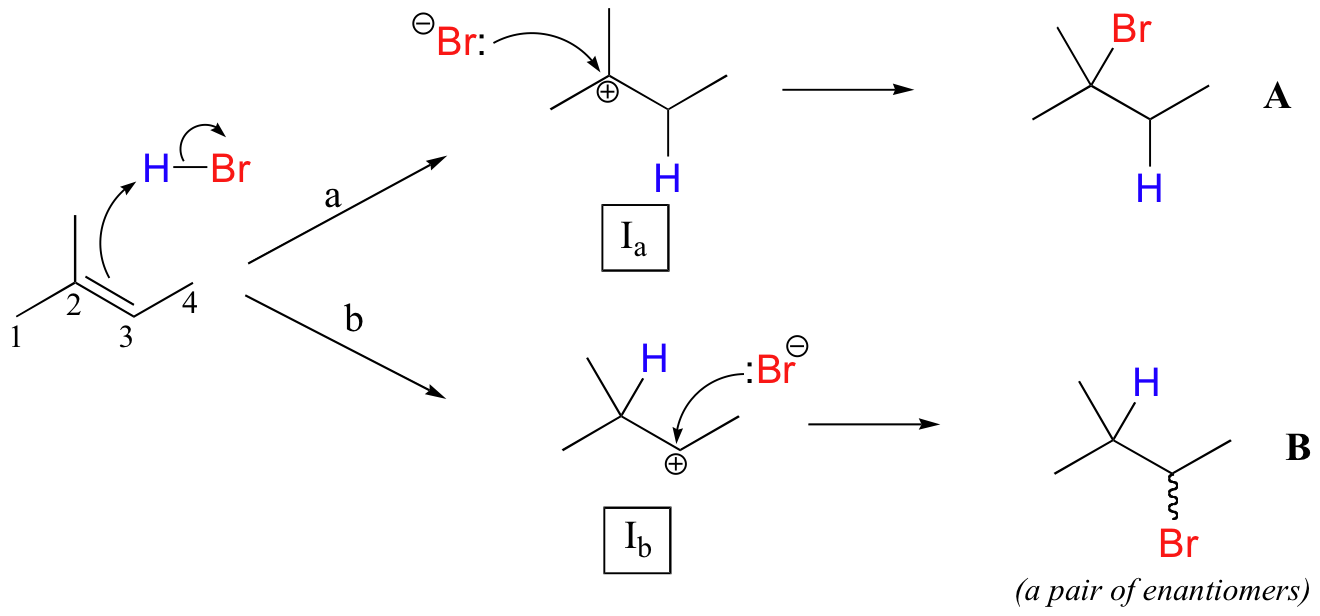
The initial protonation step could follow two different pathways, resulting in two different carbocation intermediates:  pathway 'a' gives a tertiary carbocation intermediate (I_a), while pathway 'b' gives a secondary carbocation intermediate (I_b)  We know already (section 8.4B) that the tertiary carbocation is more stable (in other words, lower in energy).  According to the Hammond postulate (section 6.2), this implies that the activation energy for pathway a is lower than in pathway b,  meaning in turn that I_a forms faster. 

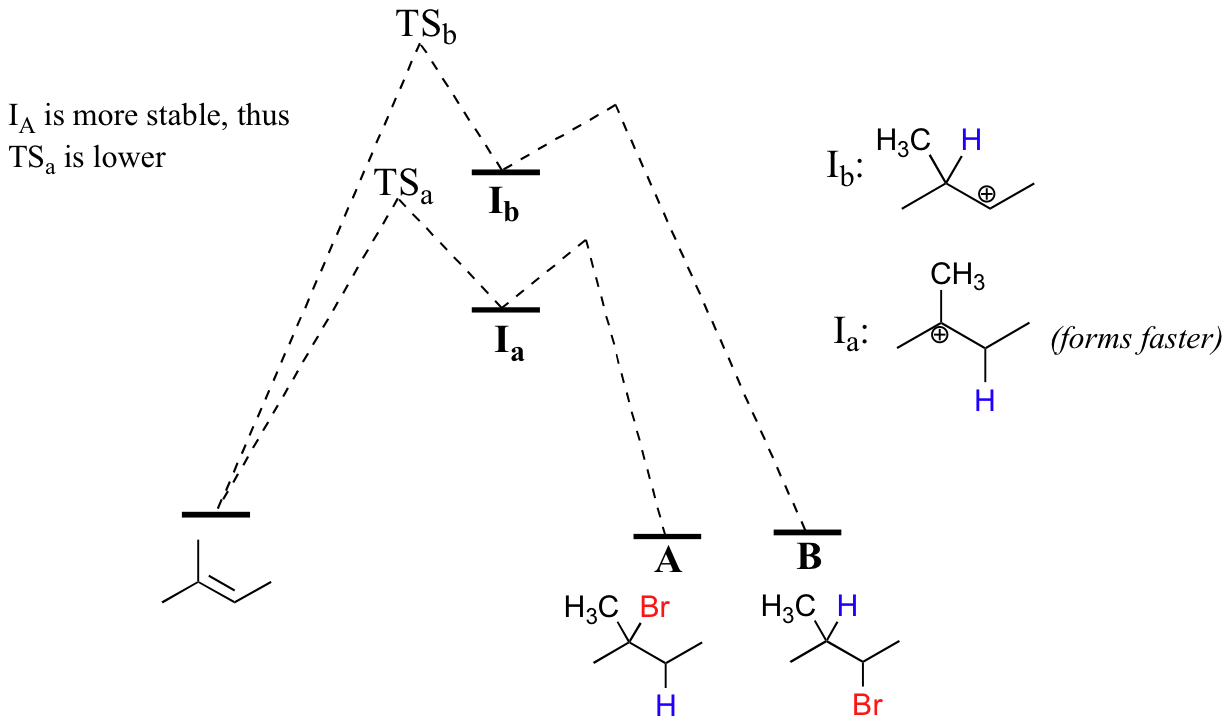
Because the protonation step is the rate determining step for the reaction, the tertiary alkyl bromide A will form much faster than the secondary alkyl halide B, and thus A will be the predominant product observed in this reaction.  This is a good example of a non-enzymatic organic reaction that is highly regiospecific.

In the example above, the difference in carbocation stability can be accounted for by the electron-donating effects of the extra methyl group on one side of the double bond. It is generally observed that, in electrophilic addition of acids (including water) to asymmetrical alkenes, the more substituted carbon is the one that ends up bonded to the heteroatom of the acid, while the less substituted carbon is protonated.

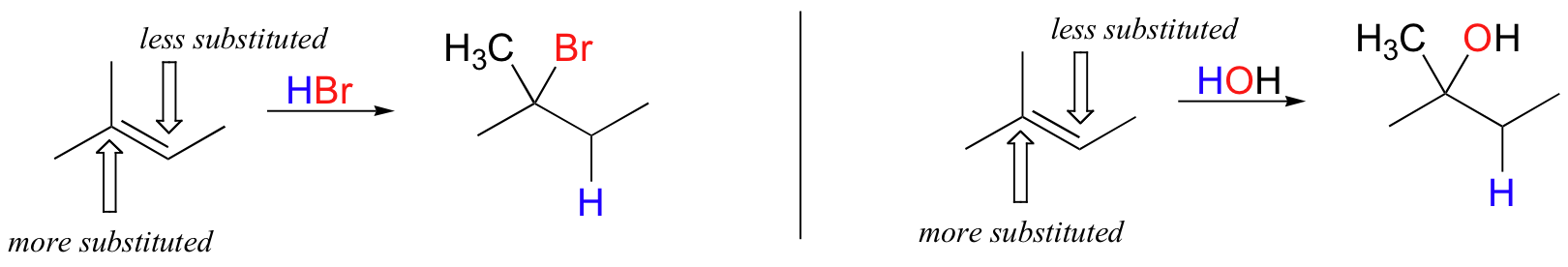
This rule of thumb is known as Markovnikov's rule, after the Russian chemist Vladimir Markovnikov who proposed it in 1869. 

While it is useful in many cases, Markovikov's rule does not apply to all possible electrophilic additions.  It is more accurate to use the more general principle that has already been stated above:

When an asymmetrical alkene undergoes electrophilic addition, the product that predominates is the one that results from the more stable of the two possible carbocation intermediates. 

How is this different from Markovnikov's original rule?  Consider the following hypothetical reaction, which is similar to the HBr addition shown above except that the six methyl hydrogens on the left side of the double bond have been replaced by highly electron-withdrawing fluorines. 

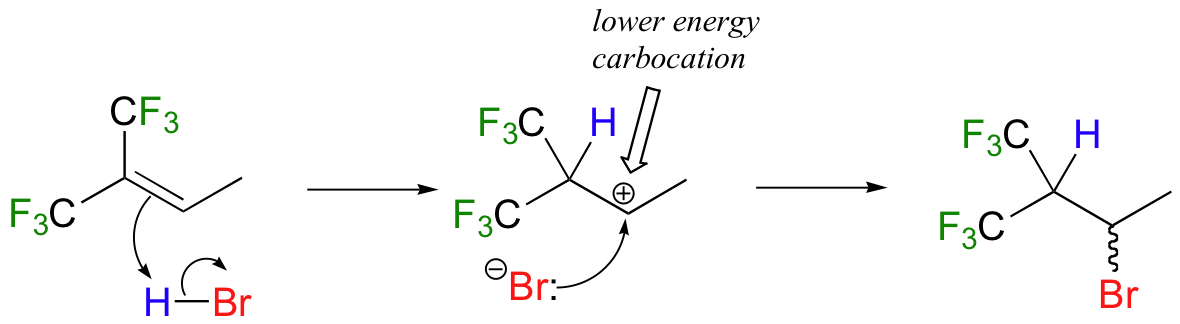
Now when HBr is added, it is the less substituted carbocation that forms faster in the rate-determining protonation step, because in this intermediate the carbon bearing the positive charge is located further away from the electron-withdrawing, cation-destabilizing fluorines.  As a result, the predominant product is the secondary rather than the tertiary bromoalkane.  This would be referred to as an 'anti-Markovnikov' addition product, because it 'breaks' Markovnikov's rule. 

Template:ExampleStart

Exercise 15.2:  Predict the product of the following reaction:

 

Template:ExampleEnd

 

15.2C: Enzymatic electrophilic additions

Enzymatic electrophilic additions are, like virtually all enzymatic reactions, highly regiospecific, a result of the precise architecture of the enzyme active site.  In most cases, biochemical pathways have evolved in such a way that electrophilic addition reactions to asymmetrical alkenes proceed through the more stable of the two possible carbocation intermediates, which of course makes the enzyme's job easier (it doesn't have to 'force' the formation of the inherently less stable intermediate).  In each of the enzymatic examples described in the following section, we will consider the inherent stability of the cationic intermediate.  Later in this chapter (section 15.8), we will discuss a very interesting strategy that many enzymes use to stabilize carbocation intermediates.

We have already seen (section 9.1A) how S-adenosyl methionine (SAM) is able to transfer a methyl group onto a nucleophilic amine or alcohol in an S_N2 reaction.  Here's an example of an electrophilic SAM-dependent methylation reaction, where the nucleophile is a pi bond on an unsaturated fatty acid. 

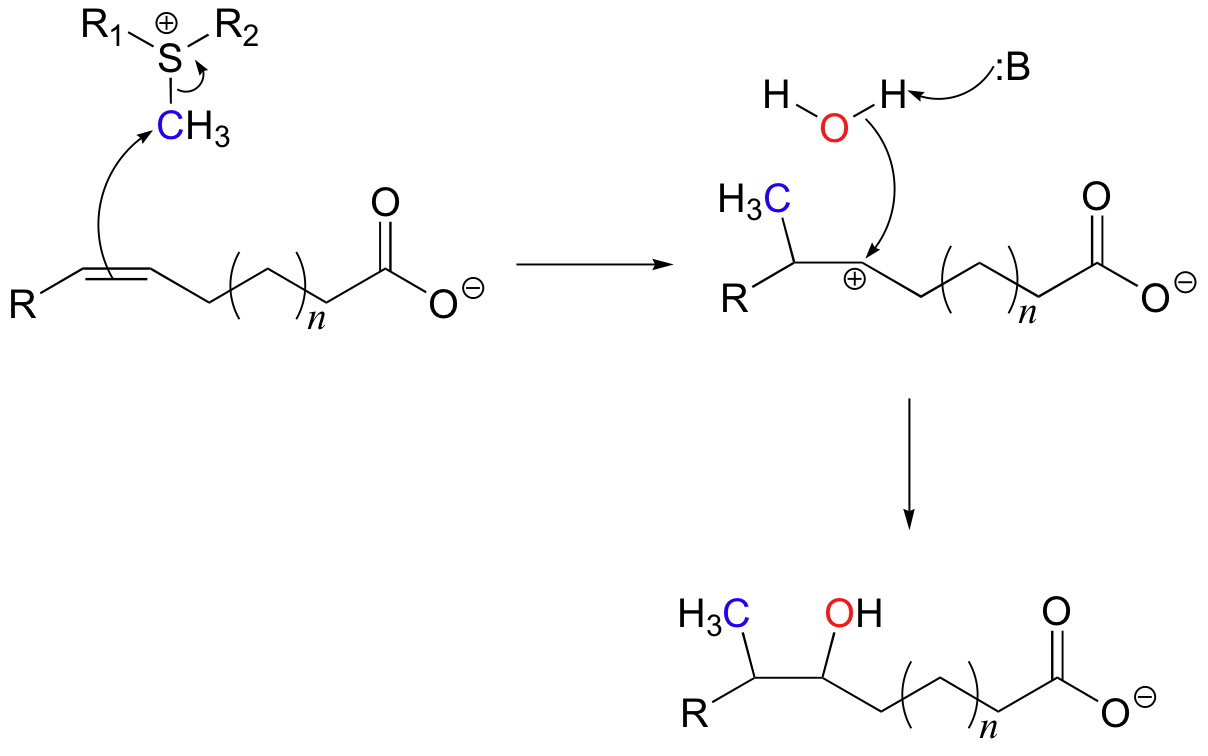
This chemical step is part the pathway by which some bacteria -including those that cause tuberculosis and leprosy - form distinctive branched-chain fatty acids for incorporation into their cell walls (J. Biol. Chem. 2006, 281, 4434).  Because the tuberculosis-causing bacterium in particular is becoming increasingly resistant to existing drugs, this enzyme is of interest to scientists working to develop new antibiotic treatments.

In this reaction, the methyl group of SAM is the electrophile which attracts the pi electrons of a double bond in an unsaturated fatty acid. Notice that the mechanism at the methyl carbon is simply an S_N2-like displacement of the sulfide leaving group, presumably with inversion of stereochemistry. Because of the symmetry in the immediate vicinity on either side of the double bond, there is not a large energy difference between the two possible carbocation intermediates that could form.  In order to form only the desired product, the enzyme must stabilize one carbocation intermediate over the other, but exactly how this is accomplished is not yet clear.  The addition is completed upon nucleophilic attack by a water molecule.

The first step in the biosynthesis of aromatic amino acids is the electrophilic addition of the four-carbon sugar erythrose-4-phosphate to the carbon-carbon double bond in phosphoenolpyruvate (PEP), a product of glycolysis.

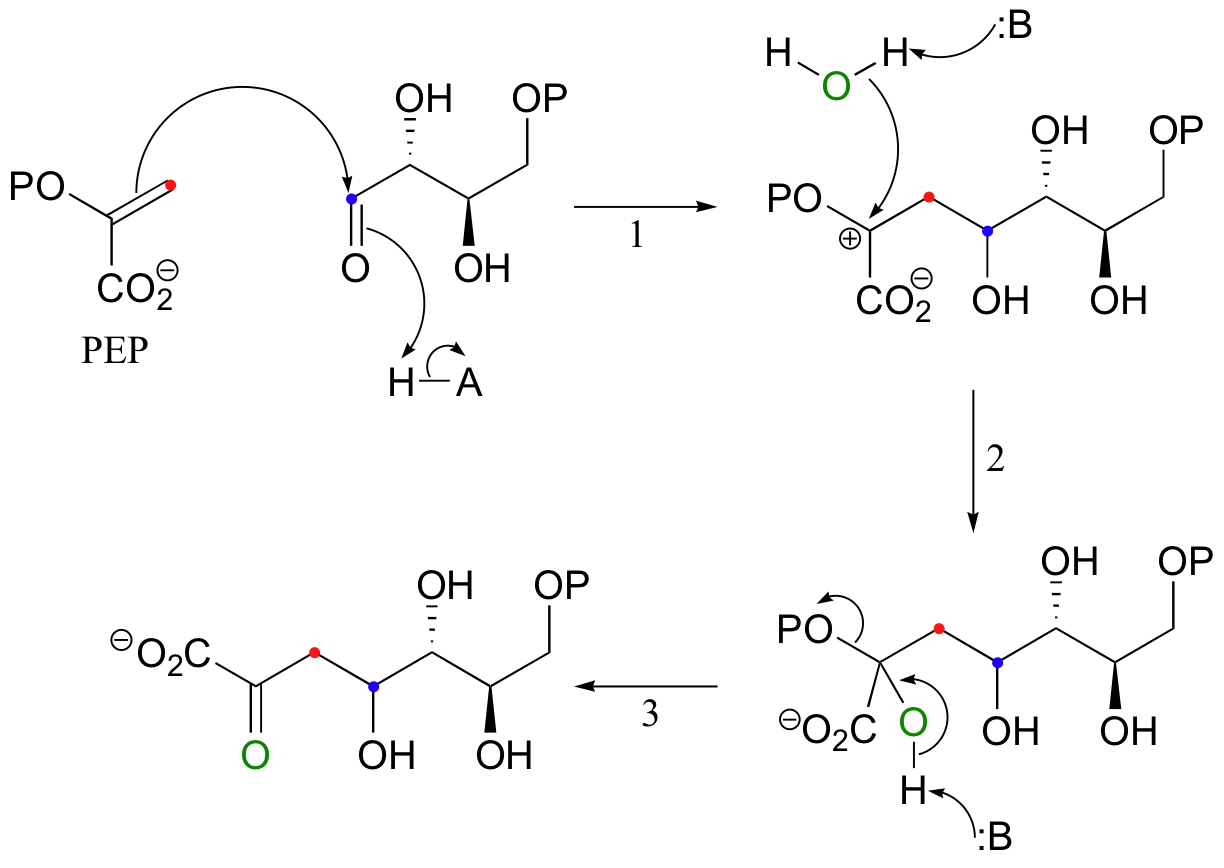
Because the pi electrons in this case are attacking an aldehyde carbonyl (step 1), this can be thought of as an electrophilic version of a carbonyl addition (chapter 11) reaction.

The addition is completed by attack of a water nucleophile (step 2), which then collapses into a carbonyl (step 3), driving off the phosphate.

The alkene substrate in this reaction (PEP) is asymmetrical, meaning that two carbocation intermediates could potentially form.  The carbocation that does form is clearly the more stable of the two, due mainly the electron-donating resonance effect of the adjacent phosphate oxygen.

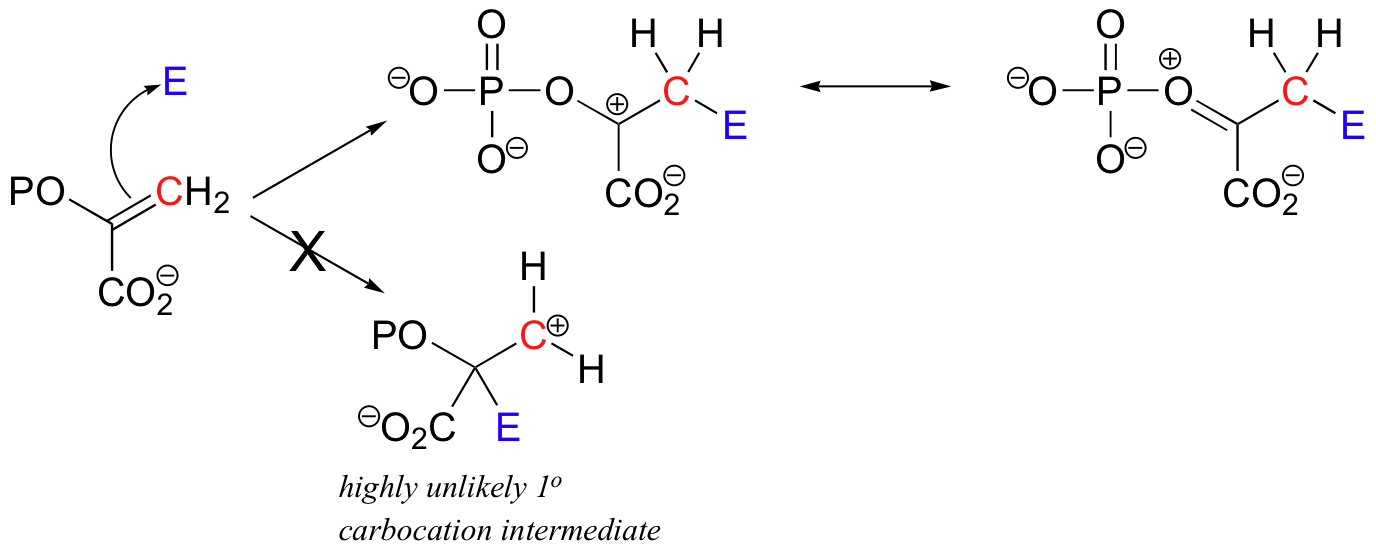
The alternative intermediate is a primary carbocation, which is a very high energy, unlikely species.

The next reaction is a good example of an intramolecular electrophilic addition: 

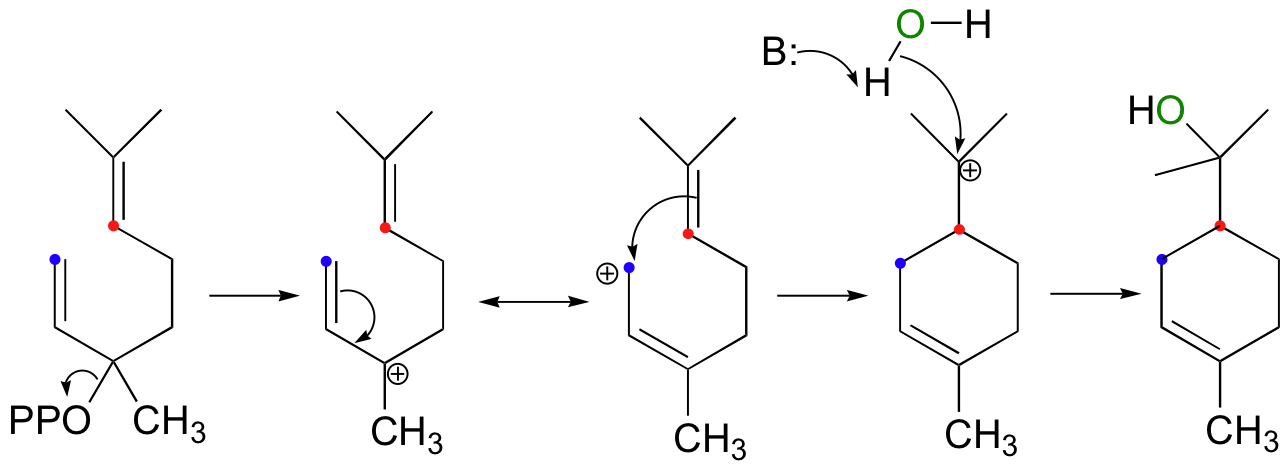
The product is alpha-terpineol, a component in sap from pine trees.  The electrophile is an allylic tertiary carbocation that is generated by the departure of pyrophosphate, an excellent leaving group. However, attack by the pi electrons does not occur directly at the carbon that was bound to the diphosphate, but instead at a carbon two positions away which bears some of the positive charge due to resonance.  Overall, this step can be described as an electrophilic version of an  S_N1' (conjugated) displacement (the S_N1' mechanism was first introduced in section 9.5). 

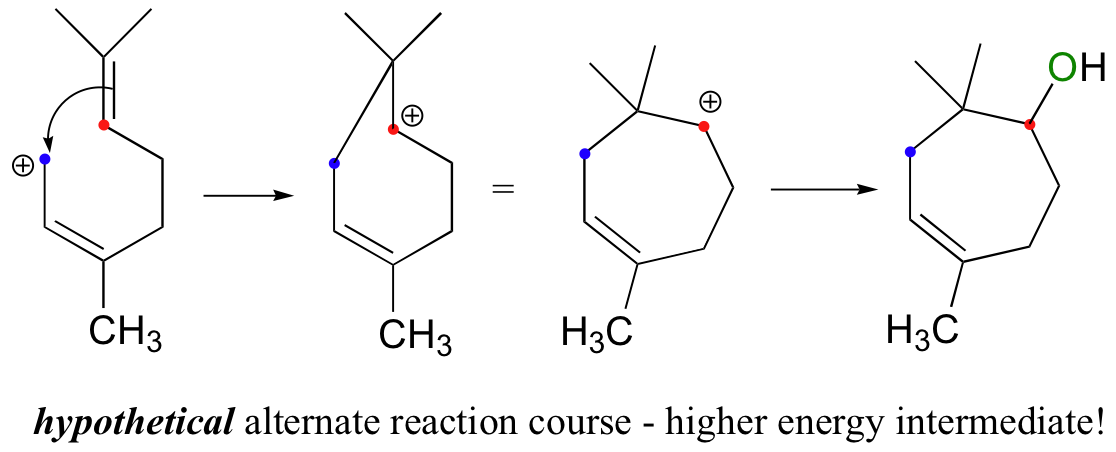
Notice another point about the regiochemical course of the reaction: as it proceeds, it results in the formation of a six-membered ring and a tertiary carbocation.  An alternate regiochemical course could result in a seven-membered ring and a secondary carbocation, a much less energetically favorable intermediate in terms of both carbocation stability and ring size (recall that six-membered rings are lower in energy then seven-membered rings).

 

15.2D: Synthetic parallel - electrophilic additions in the laboratory

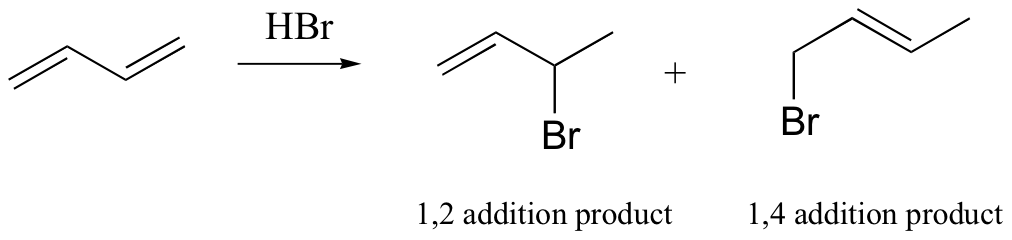
We have already seen one common laboratory electrophilic addition reaction: the addition of HBr to an alkene.  Conjugated alkenes can undergo 1,2 or 1,4 electrophilic addition:

In aqueous acid, water adds to alkenes with a similar mechanism (this is also referred to as hydration of an alkene).

Template:ExampleStart

Exercise 15.4:

a) Provide a mechanism for the addition of HBr to the alkyne shown above, and explain the regiochemical outcome.

b) Provide a mechanism for the hydration of propyne to acetone shown above.

c) Do you expect alkynes to be more or less reactive to electrophilic addition compared to alkenes?  Explain.

In the acid-catalyzed electrophilic addition of methanol to dihydropyran (DHP), the methoxy group adds to carbon 1 rather than carbon 2, because the intermediate with a positive charge on carbon 1 can be stabilized by the (resonance) electron-donating effects of the adjacent oxygen.

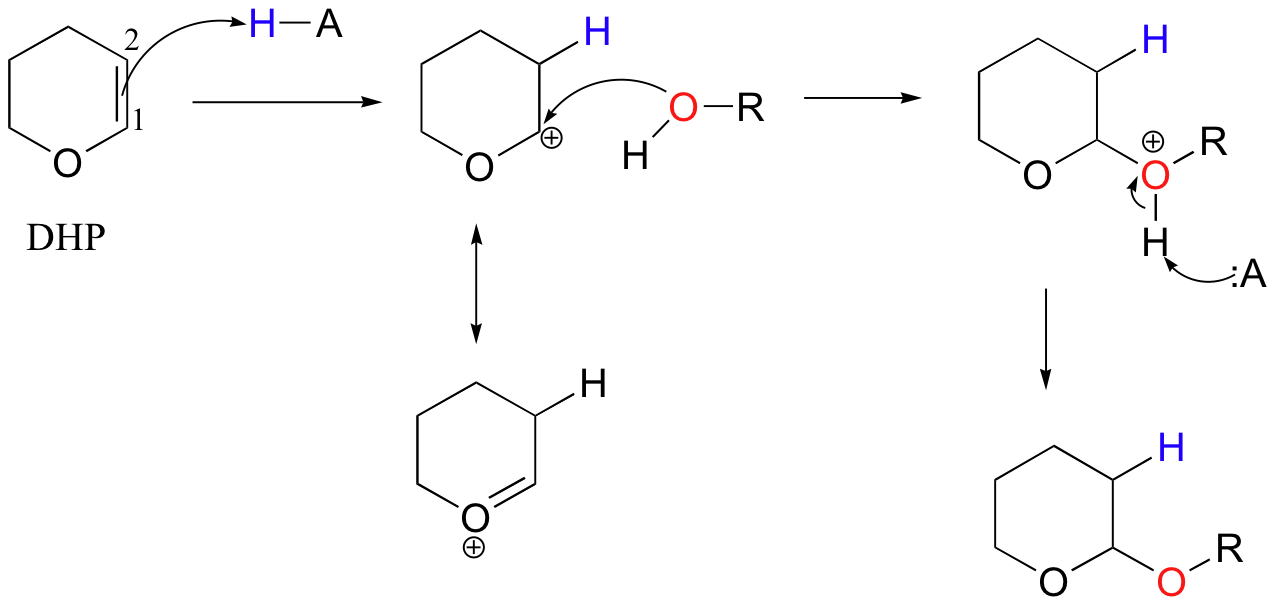
If you look carefully at this product of this reaction, you should recognize that it is a cyclic acetal (section 11.4). 

In the lab, this reaction is very useful because it serves as a method for 'protecting' an alcohol group while reactions are carried out elsewhere on the molecule under strongly basic conditions.  For example, recall that a Grignard reagent (section 13.6B) cannot be prepared from a starting material that contains an alcohol, because the Grignard reagent is highly basic (as well as nucleophilic) and would simply deprotonate the alcohol group as soon as it formed.  If, however, the alcohol group is first converted to a cyclic acetal by adding DHP, it becomes stable to strong bases and the molecule can be converted successfully into a Grignard reagent. 

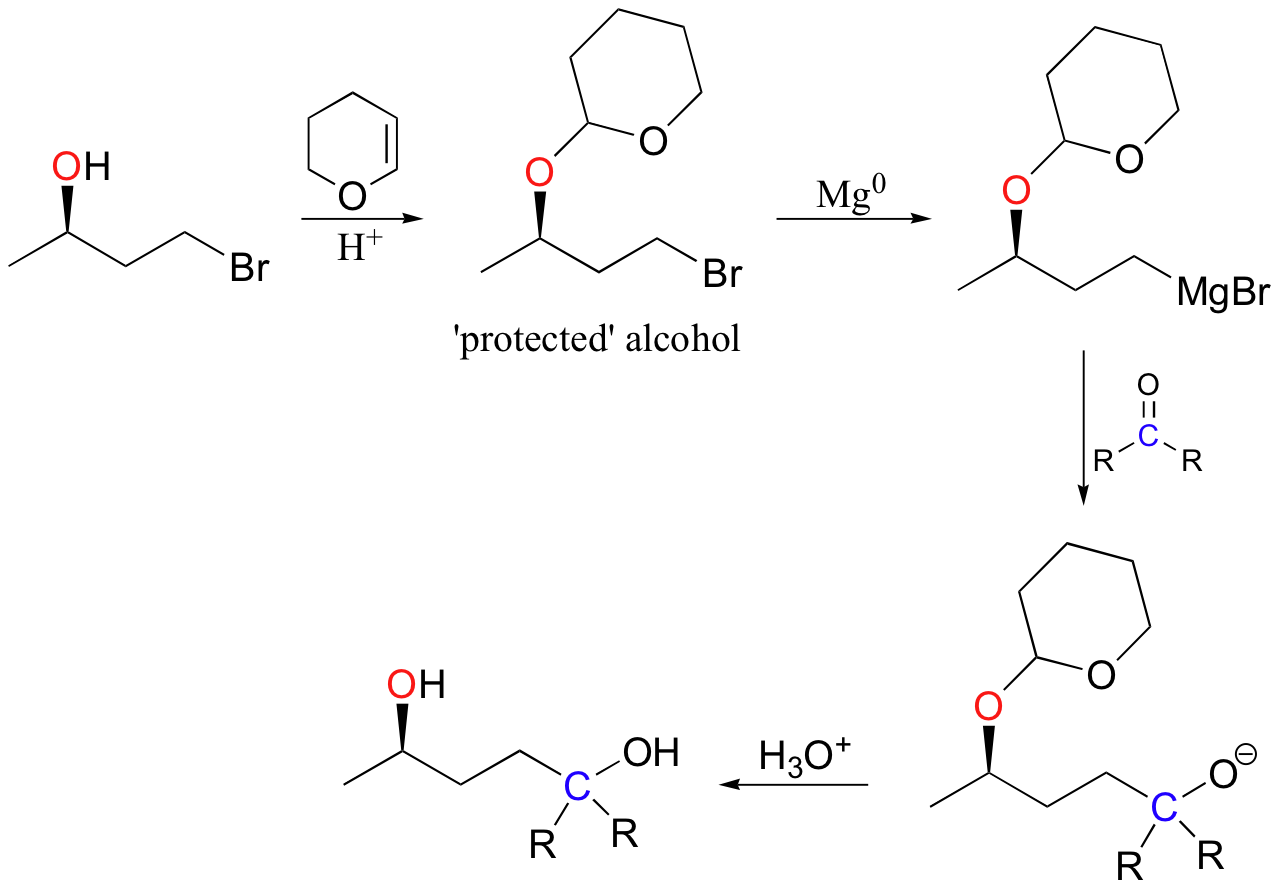
After formation of the new carbon-carbon bond, the alcohol group can be 'deprotected' by adding aqueous acid.

Template:ExampleStart

Exercise 15.5: Show a mechanism for the deprotection step (the last step) in the reaction above.

Template:ExampleStart

Exercise 15.6: Show how you could synthesize racemic 4-hydroxy-1-pentanol from  three-carbon and two-carbon starting materials.  Use a Grignard reaction and a tetrahydropyran protecting group.

Template:ExampleEnd

The following has nothing to do with electrophilic addition, but while we are on the subject of protecting groups for alcohols it is worthwhile to mention tert-butyldimethylsilyl (TBDMS) ethers.  Suppose that you wanted to deprotonate the terminal alkyne carbon on the compound below in order to turn it into a nucleophile (this type of reaction was covered in section 13.6A).  There is an obvious problem – we can’t deprotonate the terminal alkyne hydrogen without also taking the hydroxyl proton.  What we could do in this case is to first protect the alcohol group by turning it into a stable TBDMS ether – this can be accomplished with TBDMS-Cl and a simple S_N2 displacement:

 

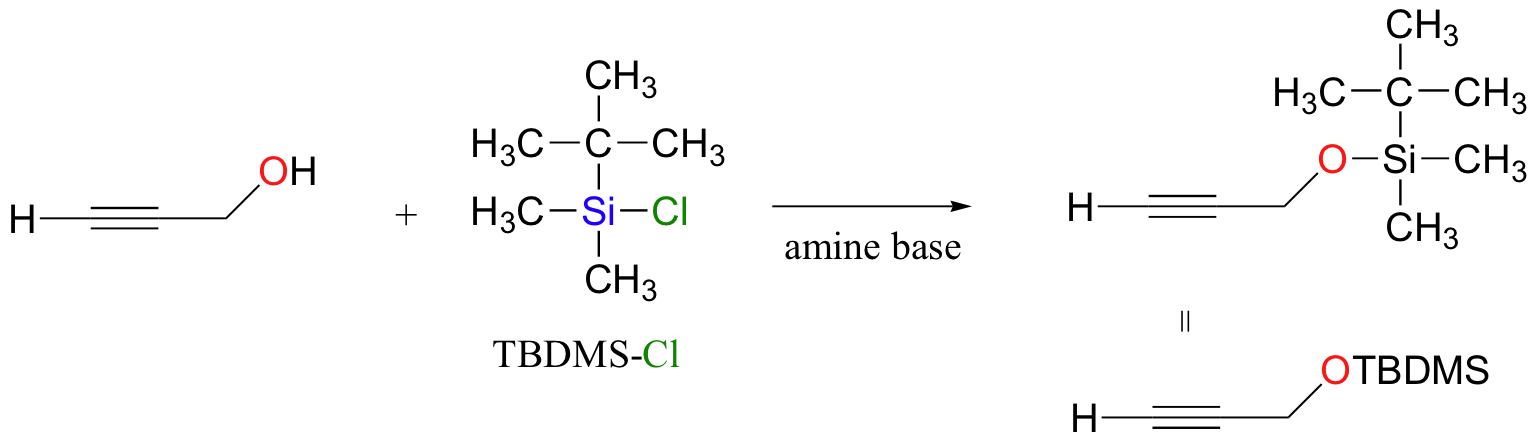
The alkyne can now be abstracted with a strong base, then used to form a new carbon-carbon bond. 

 

TBDMS ethers can be deprotected (back to an alcohol) by treatment  S_N2 with fluoride ion (typically in an ammonium salt, eg. R₄N⁺  F^-). This works because the Si-F bond is extremely strong.

 

Template:Soderberg