17.3: Standard Reduction Potentials
- Page ID
- 1937
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Habilidades para desarrollar
- Determinar los potenciales de celda estándar para las reacciones de oxidación-reducción.
- Usar los potenciales de reducción estándar para determinar el mejor agente oxidante o reductor entre varias opciones posibles
El potencial de la celda resulta de la diferencia en los potenciales eléctricos de cada electrodo. Aunque es imposible determinar el potencial eléctrico de un solo electrodo, podemos asignar a un electrodo el valor de cero y luego usarlo como referencia. El electrodo elegido como cero se muestra en la Figura 17.4.1 y se llama el electrodo de hidrógeno estándar (SHE). El SHE consiste de 1 atm de gas hidrógeno burbujeado a través de una solución de HCl 1 M, generalmente a una temperatura ambiente. El platino, que es químicamente inerte, se usa como el electrodo. La semirreacción de reducción elegida como referencia es
\[\ce{2H+}(aq,\: 1\:M)+\ce{2e-}⇌\ce{H2}(g,\:1\: \ce{atm}) \hspace{20px} E°=\mathrm{0\: V}\]
E° es el potencial de reducción estándar. El superíndice "°" en la E denota condiciones estándar (1 bar o 1 atm para gases, 1 M para solutos). El voltaje se define como cero para todas las temperaturas.

Se puede usar una celda galvánica que consiste de una semicelda de SHE y Cu2+/Cu para determinar el potencial de reducción estándar para Cu2+ (Figura \(\PageIndex{2}\)). En notación de celda, la reacción es
\[\ce{Pt}(s)│\ce{H2}(g,\:1\: \ce{atm})│\ce{H+}(aq,\:1\:M)║\ce{Cu^2+}(aq,\:1\:M)│\ce{Cu}(s)\]
Los electrones fluyen del ánodo al cátodo. Las reacciones, que son reversibles, son
&\textrm{Anode (oxidation): }\ce{H2}(g)⟶\ce{2H+}(aq) + \ce{2e-}\\
&\textrm{Cathode (reduction): }\ce{Cu^2+}(aq)+\ce{2e-}⟶\ce{Cu}(s)\\
&\overline{\textrm{Overall: }\ce{Cu^2+}(aq)+\ce{H2}(g)⟶\ce{2H+}(aq)+\ce{Cu}(s)}
\end{align*}\]
El potencial de reducción estándar se puede determinar por restando el potencial de reducción estándar para la reacción que ocurre en el ánodo del potencial de reducción estándar para la reacción que ocurre en el cátodo. El signo menos es necesario porque la oxidación es lo contrario de la reducción.
\[E^\circ_\ce{cell}=E^\circ_\ce{cathode}−E^\circ_\ce{anode}\]
\[\mathrm{+0.34\: V}=E^\circ_{\ce{Cu^2+/Cu}}−E^\circ_{\ce{H+/H2}}=E^\circ_{\ce{Cu^2+/Cu}}−0=E^\circ_{\ce{Cu^2+/Cu}}\]

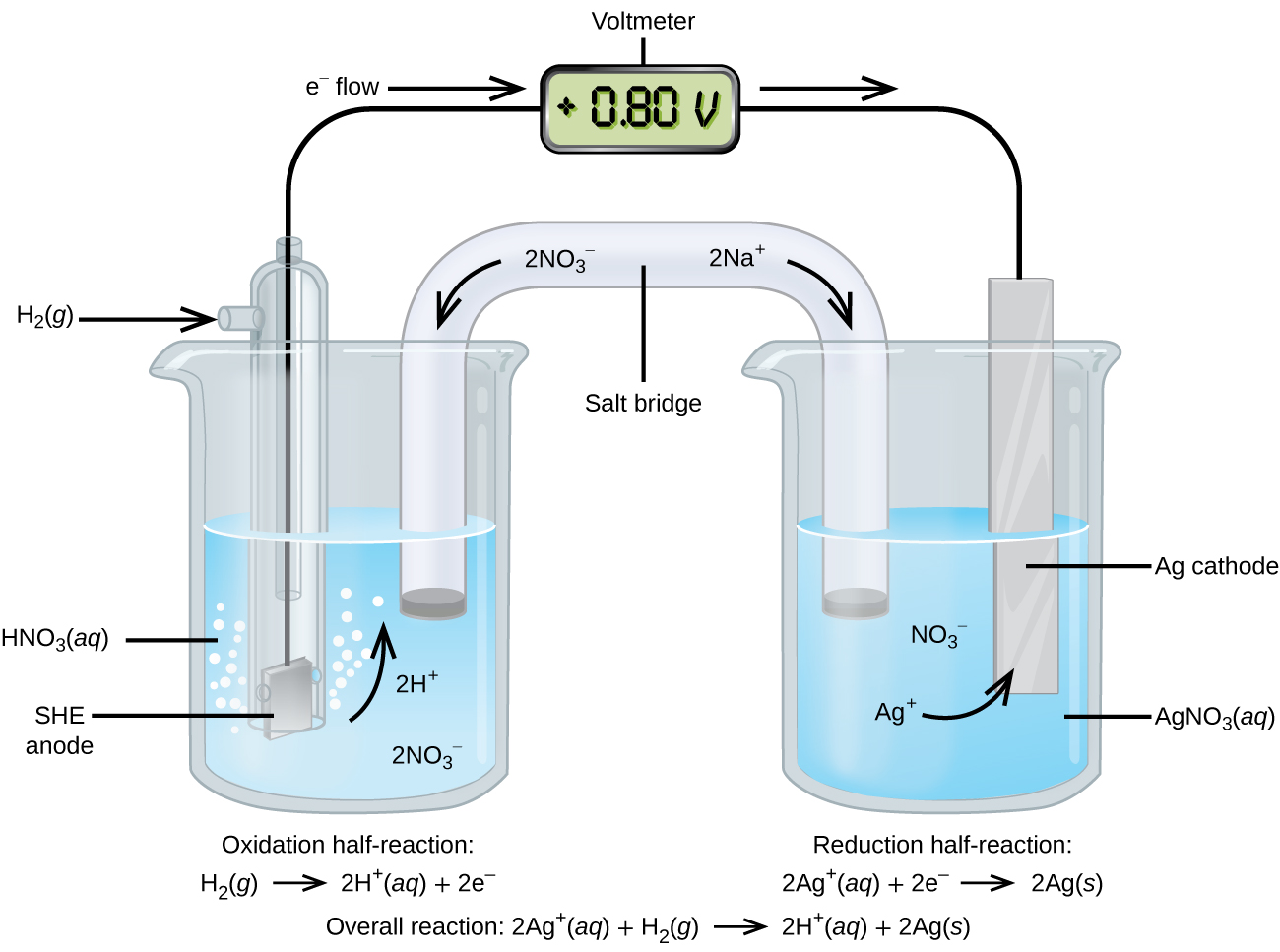
Usando el SHE como referencia, se pueden determinar otros potenciales de reducción estándar. Considere la celda que se muestra en la Figura \(\PageIndex{2}\), donde
\[\ce{Pt}(s)│\ce{H2}(g,\:1\: \ce{atm})│\ce{H+}(aq,\: 1\:M)║\ce{Ag+}(aq,\: 1\:M)│\ce{Ag}(s)\]
Los electrones fluyen de izquierda a derecha y las reacciones son
&\textrm{anode (oxidation): }\ce{H2}(g)⟶\ce{2H+}(aq)+\ce{2e-}\\
&\textrm{cathode (reduction): }\ce{2Ag+}(aq)+\ce{2e-}⟶\ce{2Ag}(s)\\
&\overline{\textrm{overall: }\ce{2Ag+}(aq)+\ce{H2}(g)⟶\ce{2H+}(aq)+\ce{2Ag}(s)}
\end{align*}\]
El potencial de reducción estándar se puede determinar por restando el potencial de reducción estándar para la reacción que ocurre en el ánodo del potencial de reducción estándar para la reacción que ocurre en el cátodo. El signo menos es necesario porque la oxidación es lo contrario de la reducción.
Es importante tener en cuenta que el potencial no se duplica para la reacción del cátodo.
El SHE es bastante peligroso y se usa raramente en el laboratorio. Su significado principal es que estableció el cero para los potenciales de reducción estándar. Una vez determinados, los potenciales de reducción estándar se pueden usar para determinar el potencial de celda estándar, \(E^\circ_\ce{celda}\), para cualquier celda. Por ejemplo, para la siguiente celda:
\[\ce{Cu}(s)│\ce{Cu^2+}(aq,\:1\:M)║\ce{Ag+}(aq,\:1\:M)│\ce{Ag}(s)\]
&\textrm{anode (oxidation): }\ce{Cu}(s)⟶\ce{Cu^2+}(aq)+\ce{2e-}\\
&\textrm{cathode (reduction): }\ce{2Ag+}(aq)+\ce{2e-}⟶\ce{2Ag}(s)\\
&\overline{\textrm{overall: }\ce{Cu}(s)+\ce{2Ag+}(aq)⟶\ce{Cu^2+}(aq)+\ce{2Ag}(s)}
\end{align*}\]
Una vez más, tenga en cuenta que al calcular \(E^\circ_\ce{celda}\), los potenciales de reducción estándar siempre permanecen iguales tambien cuando una media reacción se multiplica por un factor. Los potenciales de reducción estándar para las reacciones de reducción seleccionadas se muestran en la Tabla \(\PageIndex{1}\). Se da una lista más completa en las Tablas P1 o P2.
| Media Reaccion | E° (V) |
|---|---|
| \(\ce{F2}(g)+\ce{2e-}⟶\ce{2F-}(aq)\) | +2.866 |
| \(\ce{PbO2}(s)+\ce{SO4^2-}(aq)+\ce{4H+}(aq)+\ce{2e-}⟶\ce{PbSO4}(s)+\ce{2H2O}(l)\) | +1.69 |
| \(\ce{MnO4-}(aq)+\ce{8H+}(aq)+\ce{5e-}⟶\ce{Mn^2+}(aq)+\ce{4H2O}(l)\) | +1.507 |
| \(\ce{Au^3+}(aq)+\ce{3e-}⟶\ce{Au}(s)\) | +1.498 |
| \(\ce{Cl2}(g)+\ce{2e-}⟶\ce{2Cl-}(aq)\) | +1.35827 |
| \(\ce{O2}(g)+\ce{4H+}(aq)+\ce{4e-}⟶\ce{2H2O}(l)\) | +1.229 |
| \(\ce{Pt^2+}(aq)+\ce{2e-}⟶\ce{Pt}(s)\) | +1.20 |
| \(\ce{Br2}(aq)+\ce{2e-}⟶\ce{2Br-}(aq)\) | +1.0873 |
| \(\ce{Ag+}(aq)+\ce{e-}⟶\ce{Ag}(s)\) | +0.7996 |
| \(\ce{Hg2^2+}(aq)+\ce{2e-}⟶\ce{2Hg}(l)\) | +0.7973 |
| \(\ce{Fe^3+}(aq)+\ce{e-}⟶\ce{Fe^2+}(aq)\) | +0.771 |
| \(\ce{MnO4-}(aq)+\ce{2H2O}(l)+\ce{3e-}⟶\ce{MnO2}(s)+\ce{4OH-}(aq)\) | +0.558 |
| \(\ce{I2}(s)+\ce{2e-}⟶\ce{2I-}(aq)\) | +0.5355 |
| \(\ce{NiO2}(s)+\ce{2H2O}(l)+\ce{2e-}⟶\ce{Ni(OH)2}(s)+\ce{2OH-}(aq)\) | +0.49 |
| \(\ce{Cu^2+}(aq)+\ce{2e-}⟶\ce{Cu}(s)\) | +0.34 |
| \(\ce{Hg2Cl2}(s)+\ce{2e-}⟶\ce{2Hg}(l)+\ce{2Cl-}(aq)\) | +0.26808 |
| \(\ce{AgCl}(s)+\ce{e-}⟶\ce{Ag}(s)+\ce{Cl-}(aq)\) | +0.22233 |
| \(\ce{Sn^4+}(aq)+\ce{2e-}⟶\ce{Sn^2+}(aq)\) | +0.151 |
| \(\ce{2H+}(aq)+\ce{2e-}⟶\ce{H2}(g)\) | 0.00 |
| \(\ce{Pb^2+}(aq)+\ce{2e-}⟶\ce{Pb}(s)\) | −0.1262 |
| \(\ce{Sn^2+}(aq)+\ce{2e-}⟶\ce{Sn}(s)\) | −0.1375 |
| \(\ce{Ni^2+}(aq)+\ce{2e-}⟶\ce{Ni}(s)\) | −0.257 |
| \(\ce{Co^2+}(aq)+\ce{2e-}⟶\ce{Co}(s)\) | −0.28 |
| \(\ce{PbSO4}(s)+\ce{2e-}⟶\ce{Pb}(s)+\ce{SO4^2-}(aq)\) | −0.3505 |
| \(\ce{Cd^2+}(aq)+\ce{2e-}⟶\ce{Cd}(s)\) | −0.4030 |
| \(\ce{Fe^2+}(aq)+\ce{2e-}⟶\ce{Fe}(s)\) | −0.447 |
| \(\ce{Cr^3+}(aq)+\ce{3e-}⟶\ce{Cr}(s)\) | −0.744 |
| \(\ce{Mn^2+}(aq)+\ce{2e-}⟶\ce{Mn}(s)\) | −1.185 |
| \(\ce{Zn(OH)2}(s)+\ce{2e-}⟶\ce{Zn}(s)+\ce{2OH-}(aq)\) | −1.245 |
| \(\ce{Zn^2+}(aq)+\ce{2e-}⟶\ce{Zn}(s)\) | −0.7618 |
| \(\ce{Al^3+}(aq)+\ce{3e-}⟶\ce{Al}(s)\) | −1.662 |
| \(\ce{Mg^2}(aq)+\ce{2e-}⟶\ce{Mg}(s)\) | −2.372 |
| \(\ce{Na+}(aq)+\ce{e-}⟶\ce{Na}(s)\) | −2.71 |
| \(\ce{Ca^2+}(aq)+\ce{2e-}⟶\ce{Ca}(s)\) | −2.868 |
| \(\ce{Ba^2+}(aq)+\ce{2e-}⟶\ce{Ba}(s)\) | −2.912 |
| \(\ce{K+}(aq)+\ce{e-}⟶\ce{K}(s)\) | −2.931 |
| \(\ce{Li+}(aq)+\ce{e-}⟶\ce{Li}(s)\) | −3.04 |
Tablas como esta hacen que sea posible determinar el potencial de celda estándar para varias reacciones de oxidación-reducción
Ejemplo \(\PageIndex{1}\): Los potenciales de celda de potenciales de reducción estándar
¿Cuál es el potencial de celda estándar para una celda galvánica que consta de semiceldas de Au3+ / Au y Ni2+ / Ni? Identifique los agentes oxidantes y reductores.
Solución
Usando la tabla \(\PageIndex{1}\), las reacciones involucradas en la celda galvánica, ambas escritas como reducciones, son
\[\ce{Au^3+}(aq)+\ce{3e-}⟶\ce{Au}(s) \hspace{20px} E^\circ_{\ce{Au^3+/Au}}=\mathrm{+1.498\: V}\]
\[\ce{Ni^2+}(aq)+\ce{2e-}⟶\ce{Ni}(s) \hspace{20px} E^\circ_{\ce{Ni^2+/Ni}}=\mathrm{−0.257\: V}\]
Las celdas galvánicas tienen potenciales de celda positivos y todas las reacciones de reducción son reversibles. La reacción que ocurre en el ánodo será la semirreacción con el potencial de reducción estándar más pequeño o negativo. Invirtiendo la reacción en el ánodo (para mostrar la oxidación) pero no su potencial de reducción estándar nos dará:
\[\begin{align*}
&\textrm{Anode (oxidation): }\ce{Ni}(s)⟶\ce{Ni^2+}(aq)+\ce{2e-} \hspace{20px} E^\circ_\ce{anode}=E^\circ_{\ce{Ni^2+/Ni}}=\mathrm{−0.257\: V}\\
&\textrm{Cathode (reduction): }\ce{Au^3+}(aq)+\ce{3e-}⟶\ce{Au}(s) \hspace{20px} E^\circ_\ce{cathode}=E^\circ_{\ce{Au^3+/Au}}=\mathrm{+1.498\: V}
\end{align*}\]
El factor menos común es seis, entonces la reacción general es
Los potenciales de reducción no se escalan por los coeficientes estequiométricos cuando se calcula el potencial de la celda, y se deben usar los potenciales de reducción estándar sin modificar.
De las semirreacciones, el Ni se oxida, por eso es el agente reductor, y el Au3+ se reduce, por eso es el agente oxidante.
Ejercicio \(\PageIndex{1}\)
Una celda galvánica consiste de un electrodo de Mg en una solución de 1 M Mg(NO3)2 y un electrodo de Ag en una solución de 1 M de AgNO3. Calcule el potencial de celda estándar en 25 °C.
- Respuesta
-
\[\ce{Mg}(s)+\ce{2Ag+}(aq)⟶\ce{Mg^2+}(aq)+\ce{2Ag}(s) \hspace{20px} E^\circ_\ce{cell}=\mathrm{0.7996\: V−(−2.372\: V)=3.172\: V} \nonumber\]
Resumen
Asignar el potencial del electrodo de hidrógeno estándar (SHE) como cero voltios permite la determinación de potenciales de reducción estándar, E °, para semirreacciones en celdas electroquímicas. Como su nombre lo indica, los potenciales de reducción estándar usan estados estándar (1 bar o 1 atm para gases; 1 M para solutos, a veces a 298.15 K) y se escriben como reducciones (donde los electrones aparecen en el lado izquierdo de la ecuación). Las reacciones de reducción son reversibles, por eso los potenciales de celda estándar se pueden calcular por restando el potencial de reducción estándar para la reacción en el ánodo de la reducción estándar para la reacción en el cátodo. Al calcular el potencial de celda estándar, los potenciales de reducción estándar no se escalan por los coeficientes estequiométricos en la ecuación general equilibrada.
Ecuaciones Clave
- \(E^\circ_\ce{cell}=E^\circ_\ce{cathode}−E^\circ_\ce{anode}\)
Glosario
- potencial de celda estándar \((E^\circ_\ce{celda})\)
- el potencial de celda cuando todos los reactivos y productos están en sus estados estándar (1 bar o 1 atm o gases; 1 M para solutos), generalmente a 298.15 K; se puede calcular por restando el potencial de reducción estándar para la semirreacción en el ánodo del potencial de reducción estándar para la semirreacción que ocurre en el cátodo
- electrodo de hidrógeno estándar (SHE)
- el electrodo consiste en gas hidrógeno burbujeando a través del ácido clorhídrico sobre un electrodo inerte de platino a cuya reducción en condiciones estándar se le asigna un valor de 0 V; el punto de referencia para potenciales de reducción estándar
- potencial de reducción estándar (E °)
- el valor de la reducción en condiciones estándar (1 bar o 1 atm para gases; 1 M para solutos) generalmente a 298.15 K; valores tabulados utilizados para calcular los potenciales de celda estándar
Contribuyentes
Paul Flowers (Universidad de Carolina del Norte - Pembroke), Klaus Theopold (Universidad de Delaware) y Richard Langley (Stephen F. Austin Universidad del Estado) con autores contribuyentes. Contenido del libro de texto producido por la Universidad de OpenStax tiene licencia de Atribución de Creative Commons Licencia 4.0 licencia. Descarge gratis en http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110)."
Ana Martinez (amartinez02@saintmarys.edu) contribuyó a la traducción de este texto.


