4.2: Trabajar con números binarios

En el Capítulo 7 examinaremos varios transductores para contar fotones. Los transductores están hechos de una matriz, algunos usan una matriz lineal y otros usan una matriz bidimensional, de unidades de detección individuales. Nos preocuparemos por los detalles de cómo funcionan estos transductores en el Capítulo 7, pero si echa un vistazo rápido a la Figura 7.5.4 — 7.5.6 verá que el número de unidades de detección individuales son interesantes: una matriz lineal de 1024 unidades individuales; otra matriz lineal, pero con 2048 unidades, y una bidimensional matriz que tiene unidades\(1024 \times 1024 = 1,048,576\) individuales. Lo interesante de estos números es que cada uno es un poder de dos:\(1024 = 2^{10}\),\(2048 = 2^{11}\), y\(1,048,576 = 10^{20}\).

Los humanos se sienten cómodos trabajando con números expresados usando una notación decimal que se basa en 10 dígitos únicos (0, 1, 2, 3, 4, 5, 6, 7, 8 y 9), pero las computadoras trabajan con información usando una notación binaria que se limita a solo dos dígitos únicos (0 y 1). Aunque no completaremos cálculos usando números binarios, verá ejemplos de métodos instrumentales, como FT-NMR, donde los algoritmos de análisis de datos (la transformada de Fourier en este caso) requieren que el número de puntos de datos sea una potencia de dos. Es útil, por lo tanto, estar familiarizado con la forma en que representamos los números tanto en forma decimal como binaria.

Representación decimal de números

Mi universidad fue fundada en 1837, que es una expresión decimal del año. Cada uno de estos cuatro dígitos representa una potencia de 10, un hecho que queda claro cuando leemos el número en voz alta: mil, ochocientos, treinta y siete, o, cuando lo escribimos de esta manera

\[(1 \times 1000) + (8 \times 100) + (3 \times 10) + (7 \times 1) = 1837 \nonumber \]

o de esta manera

\[(1 \times 10^3) + (8 \times 10^2) + (3 \times 10^1) + (7 \times 10^0) = 1837 \nonumber \]

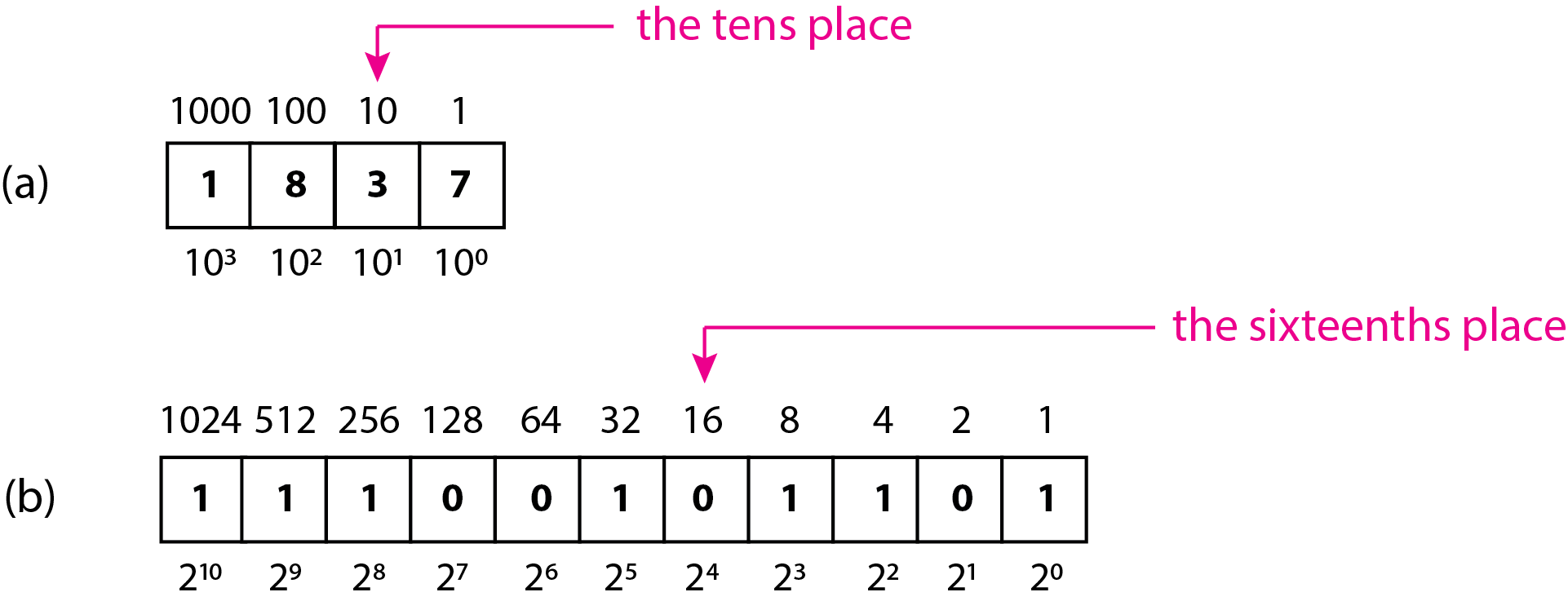
Nos referimos al 7 estando en el lugar de los unos (\(10^0 = 1\)), el 3 en el lugar de las decenas (\(10^1 = 10\)), el 8 en el lugar de los cientos (\(10^2 = 100\)), y el 1 en el lugar milésimas (\(10^3 = 1000\)). La figura\(\PageIndex{1}a\) muestra estas tres formas de representar un número usando una notación decimal.

Figura\(\PageIndex{1}\). Tres notaciones utilizadas para representar un número usando (a) dígitos decimales y potencias de 10 y (b) dígitos binarios y potencias de 2. El mismo número se representa tanto en (a) como en (b).

Representación binaria de números

El número decimal 1837 es 11100101101 en notación binaria. Podemos ver que esto es cierto si seguimos el patrón para los números decimales a la inversa. Hay once dígitos binarios, por lo que comenzamos expresando el número como múltiplos de las potencias de dos desde\(2^{10}\) hasta\(2^{0}\), comenzando con el dígito más alejado a la izquierda y moviéndonos hacia la derecha

\[(1 \times 2^{10}) + (1 \times 2^{9}) + (1 \times 2^{8}) + (0 \times 2^{7}) + (0 \times 2^{6}) + (1 \times 2^{5}) + (0 \times 2^{4}) + (1 \times 2^{3}) + (1 \times 2^{2}) + (0 \times 2^{1}) + (1 \times 2^{0}) = 1837 \nonumber \]

Cada potencia de dos tiene un equivalente decimal,\(2^4\) es lo mismo que\(2 \times 2 \times 2 \times 2 = 16\), por ejemplo, lo que podemos expresar aquí como

\[(1 \times 1024) + (1 \times 512) + (1 \times 256) + (0 \times 128) + (0 \times 64) + (1 \times 32) + (0 \times 16) + (1 \times 8) + (1 \times 4) + (0 \times 2) + (1 \times 1) = 1837 \nonumber \]

Cada potencia de dos representa también un lugar; así, el segundo 0 de la derecha está en el decimosexto lugar. La figura\(\PageIndex{1}b\) proporciona una representación visual de estas formas de expresar un número binario.

Conversión entre representaciones decimales y binarias de números

Hay muchas calculadoras en línea que puedes usar para convertir entre representaciones decimales y binarias de números, como la de aquí. Aún así, es útil estar cómodo con la conversión de números a mano. Convertir un número binario en su equivalente decimal es sencillo, como mostramos anteriormente para la representación binaria del año en que se fundó mi universidad

\[11100101101 = (1 \times 1024) + (1 \times 512) + (1 \times 256) + (0 \times 128) + (0 \times 64) + (1 \times 32) + (0 \times 16) + (1 \times 8) + (1 \times 4) + (0 \times 2) + (1 \times 1) = 1837 \nonumber \]

Convertir un número decimal, como 1837, en su equivalente binario requiere un poco más de trabajo; Table nos\(\PageIndex{1}\) ayudará a organizar la conversión. Comenzamos por escribir el dividendo, que es 1837, en la columna más a la izquierda y lo dividimos por 2, escribiendo el cociente de 918 en la segunda columna y el resto de 1 en la tercera columna; nótese que dividiendo por 2 da un resto de 0 si el dividendo es par o un resto de 1 si el dividendo es impar. El resto es el exponente para el primer lugar en la notación binaria. En este caso, tenemos\(2^0 = 1\). El cociente se convierte en el dividendo para el siguiente ciclo, con el proceso continuando hasta lograr un cociente de 0. El equivalente binario del decimal original se da leyendo los restos de abajo hacia arriba como 11100101101.

Mesa\(\PageIndex{1}\). Convertir un número binario en su equivalente decimal.

dividendo	cociente	resto	notación binaria
1837	918	1	\(2^0 = 1\)
918	459	0	\(2^1 = 1\)
459	229	1	\(2^2 = 1\)
229	114	1	\(2^3 = 1\)
114	57	0	\(2^4 = 1\)
57	28	1	\(2^5 = 1\)
28	14	0	\(2^6 = 1\)
14	7	0	\(2^7 = 1\)
7	3	1	\(2^8 = 1\)
3	1	1	\(2^9 = 1\)
1	0	1	\(2^{10} = 1\)