19.1: Teoría de la Resonancia Magnética Nuclear

Como ocurre con otras formas de espectroscopia óptica, la señal en la espectroscopia de resonancia magnética nuclear (RMN) surge de una diferencia en los niveles de energía ocupados por los núcleos en el analito. En esta sección desarrollamos una teoría general de la espectroscopia de resonancia magnética nuclear que se basa en la mecánica cuántica y en la mecánica clásica para explicar estos niveles de energía.

Descripción mecánica cuántica de RMN

La descripción mecánica cuántica de un electrón viene dada por cuatro números cuánticos: el número cuántico principal,\(n\), el número cuántico de momento angular\(l\), el número cuántico magnético,\(m_l\), y el número cuántico de espín,\(m_s\). Los tres primeros de estos números cuánticos nos dicen algo sobre dónde está el electrón relativo al núcleo y algo sobre la energía del electrón. El último de estos cuatro números cuánticos, el número cuántico de espín, nos dice algo sobre la capacidad de un electrón para interactuar con un campo magnético aplicado. Un electrón tiene posibles espines de +1/2 o de —1/2, que a menudo nos referimos como spin up, usando una flecha hacia arriba\(\uparrow\),, para representarlo, o como spin down, usando una flecha hacia abajo,\(\downarrow\), para representarlo.

Un núcleo, como un electrón, lleva una carga y tiene un número cuántico de espín. El giro general\(I\),, de un núcleo es función del número de protones y neutrones que componen el núcleo. Aquí hay tres reglas simples para los estados de giro nuclear:

• Si el número de neutrones y el número de protones son ambos números pares, entonces el núcleo no tiene espín; así, ¹² C, con seis protones y seis neutrones, no tiene giro general y\(I = 0\).
• Si el número de neutrones más el número de protones es un número impar, entonces el núcleo tiene un giro medio entero, como 1/2 o 3/2; así, ¹³ C, con seis protones y siete neutrones, tiene un giro general de\(I = 1/2\); esto también es cierto para ¹ H.
• Si el número de neutrones y el número de protones son ambos números impares, entonces el núcleo tiene un giro entero, como 1 o 2; así, ² H, con un protón y un neutrón, tiene un giro general de\(I = 1\).

Nota

Predecir que ¹³ C tiene un giro de\(I = 1/2\), pero que ¹²⁷ I tiene un giro de\(I = 3/2\) y que ¹⁷ O tiene un giro de no\(I = 5/2\) es trivial. Una tabla periódica que proporciona estados de giro para los elementos está disponible aquí.

El número total de estados de giro, es decir, el número total de posibles orientaciones del giro, es igual a\((2 \times I) + 1\). Para ser RMN activo, un núcleo debe tener al menos dos estados de espín para que sea posible un cambio en los estados de espín, y, por lo tanto, un cambio en la energía; así, ¹² C, para los cuales hay estados de\((2 \times 0) + 1 = 1\) espín, es NMR inactivo, pero ¹³ C, para lo cual hay estados de\((2 \times 1/2) + 1 = 2\) espín con valores de \(m = +1/2\)y de\(m = -1/2\), es NMR activo, como es ² H para el cual hay estados de\((2 \times 1) + 1 = 3\) espín con valores de\(m = +1/2\),\(m = 0\), y\(m = -1/2\). Como nuestro interés en este capítulo está en los espectros de RMN para ¹ H y para ¹³ C, nos limitaremos a considerar\(I = 1/2\) y girar estados de\(m = +1/2\) y de\(m = -1/2\).

Niveles de energía en un campo magnético aplicado

Supongamos que tenemos una gran población de ¹ átomos de H. En ausencia de un campo magnético aplicado los átomos se dividen equitativamente entre sus posibles estados de espín: 50% de los átomos tienen un espín de +1/2 y 50% de los átomos tienen un espín de —1/2. Ambos estados de espín tienen la misma energía, como es el caso del lado izquierdo de la Figura\(\PageIndex{1}\), y no se produce absorción ni emisión.

Figura\(\PageIndex{1}\). Diagrama de nivel de energía para un protón, ¹ H, en ausencia (izquierda) y en presencia (derecha) de un campo magnético aplicado.

En presencia de un campo magnético aplicado, como en el lado derecho de la Figura\(\PageIndex{1}\), los núcleos están alineados con el campo magnético con espines de\(m = +1/2\), o alineados contra el campo magnético con espines de\(m = -1/2\). Las energías en estos dos estados de giro,\(E_\text{lower}\) y\(E_\text{upper}\), están dadas por las ecuaciones

\[E_\text{lower} = - \frac{\gamma h}{4 \pi}B_0 \label{nmr1} \]

\[E_\text{upper} = + \frac{\gamma h}{4 \pi}B_0 \label{nmr2} \]

donde\(\gamma\) es la relación magnetogírica para el núcleo,\(h\) es la constante de Planck, y\(B_0\) es la fuerza del campo magnético aplicado. La diferencia en energía,\(\Delta E\), entre los dos estados es

\[\Delta E = E_\text{upper} - E_\text{lower} = + \frac{\gamma h}{4 \pi}B_0 - \left( - \frac{\gamma h}{4 \pi}B_0 \right) = \frac{\gamma h}{2 \pi}B_0 \label{nmr3} \]

Sustituir la ecuación\ ref {nmr3} en la ecuación más familiar\(\Delta E = h \nu\) da la frecuencia,\(\nu\), de la radiación electromagnética necesaria para efectuar un cambio en el estado de giro como

\[\nu = \frac{\gamma B_0}{2 \pi} \label{nmr4} \]

A esto se le llama la frecuencia de Larmor para el núcleo. Por ejemplo, si el imán tiene una intensidad de campo de 11.74 Tesla, entonces la frecuencia necesaria para efectuar un cambio en el estado de giro para ¹ H, para lo cual\(\gamma\) es\(2.68 \times 10^8 \text{ rad}\text{ T}^{-1} \text{s}^{-1}\), es

\[\nu = \frac{(2.68 \times 10^8 \text{rad} \text{ T}^{-1}\text{s}^{-1})(11.74 \text{ T})}{2 \pi} = 5.01 \times 10^8 \text{ s}^{-1} \nonumber \]

o 500 MHz, que se encuentra en el rango de radiofrecuencia (RF) del espectro electromagnético. Esta es la frecuencia Larmor para ¹ H.

Población de Spin States

La población relativa del estado de espín superior\(N_\text{upper}\), y del estado de espín inferior\(N_\text{lower}\), viene dada por la ecuación de Boltzmann

\[\frac{N_\text{upper}}{N_\text{lower}} = e^{- \Delta E/k T} \label{nmr5} \]

donde\(k\) es la constante de Boltzmann (\(1.38066 \times 10^{-23} \text{ J/K}\)) y\(T\) es la temperatura en Kelvin. Sustituyendo en la Ecuación\ ref {nmr3} para\(\Delta E\) da esta relación como

\[\frac{N_\text{upper}}{N_\text{lower}} = e^{-\gamma h B_0/2 \pi k T} \label{nmr6} \]

SI colocamos una población de átomos de ¹ H en un campo magnético con una intensidad de 11.74 Tesla, la relación\(\frac{N_\text{upper}}{N_\text{lower}}\) a 298 K es

\[\frac{N_\text{upper}}{N_\text{lower}} = e^{-\frac{(2.68 \times 10^{8} \text{ rad} \text{ s}^{-1})(6.626 \times 10^{-34} \text{ Js})(11.74 \text{ T})}{(2 \pi)(1.38 \times 10^{-23} \text{ JK}^{-1})(298 \text{ K})}} = 0.99992 \nonumber \]

Si esta relación es 1:1, entonces la probabilidad de absorción y emisión son iguales y no hay señal neta. En este caso, la diferencia en las poblaciones es del orden de 8 por 100 mil, o 80 por 1,000,000, o 80 ppm. La pequeña diferencia en las dos poblaciones significa que la RMN es menos sensible que muchos otros métodos espectroscópicos.

Descripción clásica de RMN

Para entender la descripción clásica de un experimento de RMN nos basamos en la Figura\(\PageIndex{2}\). Por simplicidad, supongamos que en la población de núcleos disponibles para nosotros, hay un exceso de solo un núcleo con un estado de espín de +1/2. En la Figura\(\PageIndex{2}a\), vemos que el giro de este núcleo no está perfectamente alineado con el campo magnético aplicado\(B_0\), que está alineado con el eje z; en cambio el núcleo precede alrededor del eje z en un ángulo de theta,\(\Theta\). Como resultado, el momento magnético neto a lo largo del eje z\(\mu_z\),, es menor que el momento magnético, µ, del núcleo. La precesión ocurre con una velocidad angular,\(\omega_0\), de\(\gamma B_0\).

Figura\(\PageIndex{2}\). Ilustración que muestra en (a) el momento magnético, µ, de un núcleo cuyo giro está alineado con el campo magnético aplicado,\(B_0\). Aplicación del campo magnético,\(B_1\) voltea el giro del núcleo, como se muestra en (b).

Si aplicamos una fuente de radiación electromagnética de radiofrecuencia (RF) a lo largo del eje x de tal manera que su componente de campo magnético\(B_1\),\(B_0\), sea perpendicular a, entonces generará su propia velocidad angular en el plano xy. Cuando la velocidad angular del núcleo de precesión coincide con la velocidad angular de\(B_1\), se produce la absorción y el giro gira, como se ve en la Figura\(\PageIndex{2}b\).

Relajación

Cuando\(B_1\) se elimina el campo magnético, el núcleo vuelve a su estado original, como se ve en la Figura\(\PageIndex{2}a\), un proceso llamado relajación. En ausencia de relajación, el sistema se satura con poblaciones iguales de los dos estados de espín y la absorción se aproxima a cero. Este proceso de relajación tiene dos mecanismos separados: relajación de espín-celosía y relajación de espín-espín.

En la relajación de espín-celosía el núcleo en su estado de espín de mayor energía\(\PageIndex{2}b\), FIGURA, vuelve a su estado de giro de menor energía\(\PageIndex{2}a\), Figura, al transferir energía a otras especies presentes en la muestra (la celosía en espín-celosía). La relajación de espín-celosía se caracteriza por una decadencia exponencial de primer orden con un tiempo de relajación característico\(T_1\) que es una medida del tiempo promedio que el núcleo permanece en su estado de giro de mayor energía. Valores más pequeños para\(T_1\) dar como resultado una relajación más eficiente.

Si dos núcleos del mismo tipo, pero en diferentes estados de espín, están muy próximos entre sí, pueden comerciar lugares en los que el núcleo en el estado de giro de mayor energía cede su energía al núcleo en el estado de giro de energía inferior. El resultado es una disminución en el tiempo promedio de vida de un estado excitado. Esto se llama relajación spin-spin y se caracteriza por un tiempo de relajación de\(T_2\).

RMN de onda continua frente a RMN de transformada de Fourier

En el Capítulo 16 aprendimos que podemos registrar un espectro infrarrojo mediante el uso de un monocromador de barrido para pasar, secuencialmente, diferentes longitudes de onda de radiación IR a través de una muestra, obteniendo un espectro de absorbancia en función de la longitud de onda. También aprendimos que podemos obtener el mismo espectro pasando todas las longitudes de onda de radiación IR a través de la muestra al mismo tiempo usando un interferómetro, y luego usar una transformada de Fourier para convertir el interferograma resultante en un espectro de absorbancia en función de la longitud de onda. Aquí consideramos sus equivalentes para espectroscopía de RMN.

RMN de onda continua

Si escaneamos\(B_1\) mientras mantenemos\(B_0\) constante, o escaneamos\(B_0\) mientras\(B_1\) mantenemos constantes, entonces podemos identificar las frecuencias de Larmor donde absorbe un núcleo en particular. El resultado es un espectro de RMN que muestra la intensidad de absorción en función de la frecuencia a la que tiene lugar esa absorción. Debido a que registramos el espectro escaneando a través de un continuo de frecuencias, el método se conoce como RMN de onda continua. La Figura\(\PageIndex{2}\) proporciona una visualización útil para este experimento.

RMN de transformada de Fourier

En la RMN de transformada de Fourier, el campo magnético\(B_1\) se aplica como un breve pulso de radiación electromagnética de radiofrecuencia (RF) centrada a una frecuencia apropiada para el núcleo de interés y para la intensidad del campo magnético primario,\(B_0\). El pulso típicamente es de 1-10 µs de longitud y se aplica en el plano xy. Desde el principio de incertidumbre de Heisenberg, un pulso corto de\(\Delta t\) resulta en un amplio rango de frecuencias ya que\(\Delta f = 1/\Delta t\); esto asegura que el pulso abarque un rango suficiente de frecuencias tal que el núcleo de interés para nosotros absorba energía y entre en un estado excitado.

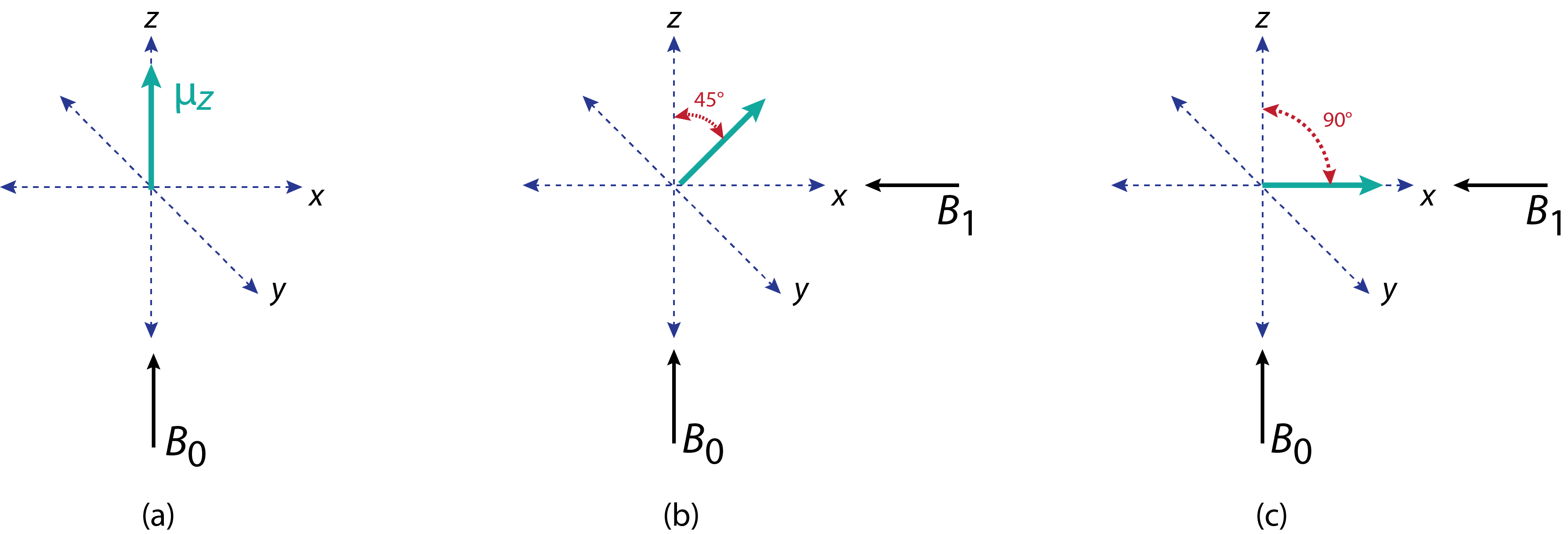
Antes de aplicar el pulso, la población de núcleos se alinea paralela al campo magnético aplicado\(B_0\), algunos con un giro de +1/2 y otros con un giro de —1/2. Como aprendimos anteriormente, existe un ligero exceso de núcleos con espines de +1/2, que podemos representar como un solo vector que muestra sus momentos magnéticos combinados a lo largo del eje z\(\mu_z\), como se muestra en la Figura\(\PageIndex{3}a\). Cuando aplicamos un pulso de radiación electromagnética de RF con una intensidad de campo magnético de\(B_1\), los estados de espín de los núcleos se alejan del eje z en un ángulo que depende de la relación magnetogírica del núcleo\(\gamma\), el valor de\(B_1\), y la longitud del pulso. Si, por ejemplo, un pulso de 5 µs inclina el vector magnético 45° (Figura\(\PageIndex{3}b\)), entonces un pulso de 10 µs inclinará el vector magnético 90° grados (Figura\(\PageIndex{3}c\)), de manera que ahora se encuentra completamente dentro del plano xy.

Figura\(\PageIndex{3}\). Ilustración que muestra (a) el momento magnético neto en el eje z para una población de núcleos en un campo magnético aplicado con una intensidad de campo de\(B_0\). La aplicación de un campo de RF pulsado\(B_1\), inclina el momento magnético (b) lejos del eje z. Cuanto más largo sea el pulso de RF, mayor será el ángulo de inclinación, como se muestra en (c).

Al final del pulso, los núcleos comienzan a relajarse de nuevo a su estado original. La figura\(\PageIndex{4}\) muestra que esta relajación ocurre tanto en el plano xy (relajación de espín-espín) como a lo largo del eje z (relajación de espín-retícula). Si tuviéramos que trazar la trayectoria del vector magnético con el tiempo, veríamos que sigue un movimiento en espiral a medida que su contribución en el plano xy disminuye y su contribución a lo largo del eje z aumenta. Medimos esta señal, llamada decaimiento de inducción libre, o FID, durante este período de relajación.

Figura\(\PageIndex{4}\). Ilustración que muestra el proceso de relajación durante un experimento de RMN. La fila inferior muestra el momento magnético neto alineado con el eje z,\(\mu_z\), en función del tiempo. La fila superior muestra el momento magnético neto en el plano xy con la figura en la parte superior derecha mostrando el cambio general en el momento magnético neto en tres dimensiones.

El FID para un sistema que consiste en un solo tipo de núcleo es la simple señal oscilante amortiguada exponencialmente en la Figura\(\PageIndex{5}a\). La transformada de Fourier de este FID simple da el espectro en la Figura\(\PageIndex{5}b\) que tiene un solo pico. Una muestra con más de un tipo de núcleo produce un patrón FID más complejo, como el de la Figura\(\PageIndex{5}c\), y un espectro más complejo, como los dos picos de la Figura\(\PageIndex{5}d\). Tenga en cuenta que, como aprendimos en un tratamiento anterior de la transformada de Fourier en el Capítulo 7, un pico más amplio en el dominio de la frecuencia da como resultado una disminución más rápida en el dominio del tiempo.

Figura\(\PageIndex{5}\). Los paneles (a) y (b) muestran la señal FID para una muestra que rinde un solo pico y el resultado de tomar el FT del FID. Los paneles (c) y (d) muestran la señal FID para una muestra que consta de dos picos y el resultado de tomar el FT del FID.

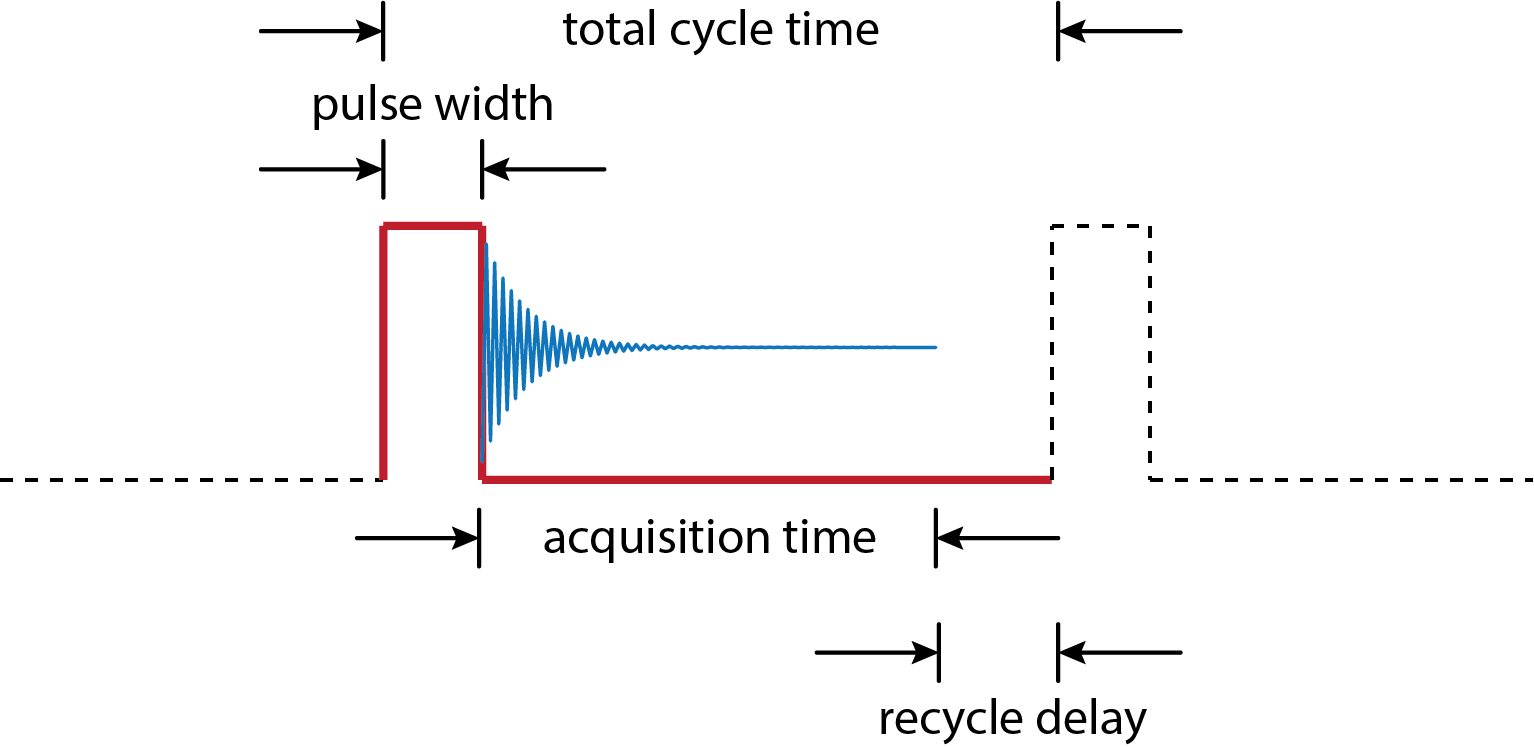
La figura\(\PageIndex{6}\) muestra una secuencia típica de pulsos que destaca el tiempo total del ciclo y sus partes componentes: el ancho de pulso, el tiempo de adquisición durante el cual se registra el FID y un retardo de reciclaje antes de aplicar el siguiente pulso e iniciar el siguiente ciclo.

Figura\(\PageIndex{1}\): Ejemplo de una secuencia de pulsos.