35.7: Coeficientes de actividad

Mediciones cuidadosas en el complejo metal-ligando Fe (SCN) ²⁺ sugieren que su estabilidad disminuye en presencia de iones inertes [Lister, M. W.; Rivington, D. E. Can. J. Chem. 1995, 33, 1572—1590]. Podemos demostrar esto agregando una sal inerte a una mezcla de equilibrio de Fe ^{3 +} y SCN ^—. La Figura 35.7.1 a muestra el resultado de mezclar juntos volúmenes iguales de FeCl ₃ 1.0 mM y KSCN 1.5 mM, ambos de los cuales son incoloros. El color rojizo anaranjado de la solución se debe a la formación de Fe (SCN) ²⁺.

\[\mathrm{Fe}^{3+}(a q)+\mathrm{SCN}^{-}(a q) \rightleftharpoons \mathrm{Fe}(\mathrm{SCN})^{2+}(a q) \label{6.1} \]

Figura 35.7.1 . El efecto de una sal inerte sobre la posición de equilibrio de una reacción se muestra por las soluciones en estos dos vasos de precipitados. El vaso de precipitados de la izquierda contiene volúmenes iguales de 1.0 mM de FeCl ₃ y 1.5 mM de KSCN. El color de la solución se debe a la formación del complejo metal-ligando Fe (SCN) ²⁺. Al agregar 10 g de KNO ₃ al vaso de precipitados de la izquierda se obtiene el resultado que se muestra a la derecha. El color más claro sugiere que hay menos Fe (SCN) ²⁺ como resultado del equilibrio en la reacción\ ref {6.1} desplazándose hacia la izquierda.

Agregar 10 g de KNO ₃ a la solución y agitar para disolver el sólido, produce el resultado mostrado en la Figura 35.7.1 b. El color más claro de la solución sugiere que agregar KNO ₃ desplaza la reacción\ ref {6.1} a la izquierda, disminuyendo la concentración de Fe (SCN) ²⁺ y aumentando las concentraciones de Fe ^{3 +} y SCN ^—. El resultado es una disminución en la constante de formación del complejo, K ₁.

\[K_{1}=\frac{\left[\mathrm{Fe}(\mathrm{SCN})^{2+}\right]}{\left[\mathrm{Fe}^{3+}\right]\left[\mathrm{SCN}^{-}\right]} \label{6.2} \]

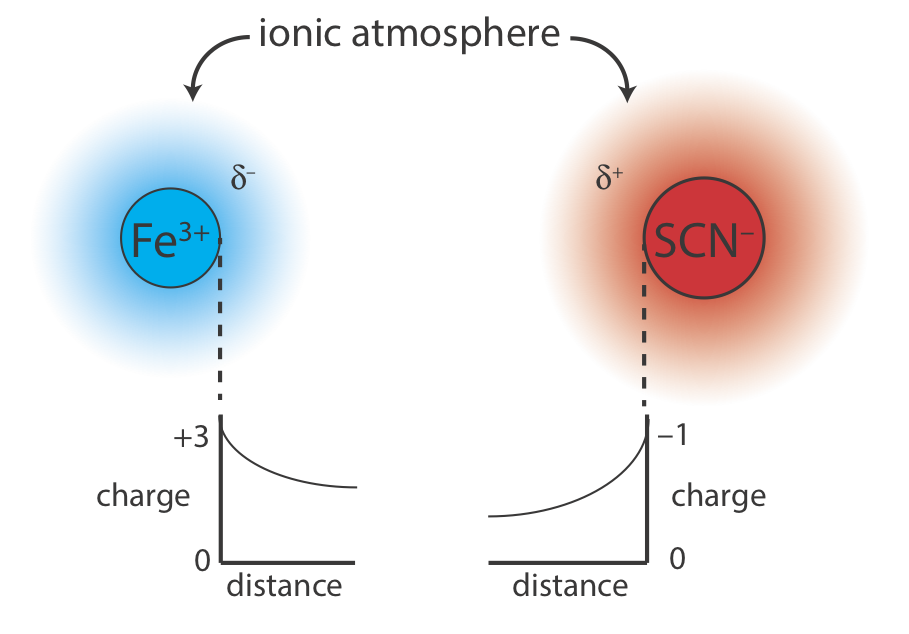
¿Por qué la adición de un electrolito inerte debería afectar la posición de equilibrio de una reacción? Podemos explicar el efecto del KNO ₃ sobre la formación de Fe (SCN) ²⁺ si consideramos la reacción a escala microscópica. La solución en la Figura 35.7.1 b contiene una variedad de cationes y aniones: Fe ^{3 +}, SCN ^—, K ⁺\(\text{NO}_3^-\),, H ₃ O ⁺ y OH ^—. ^{Si bien la solución es homogénea, en promedio, hay un poco más de aniones en regiones cercanas a los iones Fe 3 +, y un poco más de cationes en regiones cercanas a los iones SCN. Como se muestra en la Figura 35.7.2 , cada ion Fe 3 + y cada ion SCN está rodeado por una atmósfera iónica de carga opuesta (\(\delta^–\)y\(\delta^+\)) que criba parcialmente los iones entre sí.} Debido a que la carga aparente de cada ion en el borde de su atmósfera iónica es menor que su carga real, la fuerza de atracción entre los dos iones es menor. Como resultado, la formación de Fe (SCN) ²⁺ es ligeramente menos favorable y la constante de formación en la Ecuación\ ref {6.2} es ligeramente menor. Las concentraciones más altas de KNO ₃ aumentan\(\delta^–\) y\(\delta^+\), dando como resultado valores aún más pequeños para la constante de formación.

Figura 35.7.2 . Los iones de Fe ^{3 +} y SCN ^- están rodeados de atmósferas iónicas con cargas netas de\(\delta^–\) y\(\delta^+\). Debido a estas atmósferas iónicas, la carga aparente de cada ion en el borde de su atmósfera iónica es menor que la carga real del ion.

Fuerza iónica

Para factorizar la concentración de iones en la constante de formación para Fe (SCN) ²⁺, necesitamos una forma de expresar esa concentración de manera significativa. Debido a que tanto la concentración de un ion como su carga son importantes, definimos la fuerza iónica de la solución,\(\mu\) como

\[\mu=\frac{1}{2} \sum_{i=1}^{n} c_{i} z_{i}^{2} \nonumber \]

donde c _i y z _i son la concentración y carga del ión ^i-ésimo.

Ejemplo 35.7.1

Calcular la fuerza iónica de una solución de NaCl 0.10 M. Repetir el cálculo para una solución de 0.10 M Na ₂ SO ₄.

Solución

La fuerza iónica para NaCl 0.10 M es

\[\begin{array}{c}{\mu=\frac{1}{2}\left\{\left[\mathrm{Na}^{+}\right] \times(+1)^{2}+\left[\mathrm{Cl}^{-}\right] \times(-1)^{2}\right\}} \\ {\mu=\frac{1}{2}\left\{(0.10) \times(+1)^{2}+(0.10) \times(-1)^{2}\right\}=0.10 \ \mathrm{M}}\end{array} \nonumber \]

Para 0.10 M Na ₂ SO ₄ la fuerza iónica es

\[\begin{array}{c}{\mu=\frac{1}{2}\left\{\left[\mathrm{Na}^{+}\right] \times(+1)^{2}+\left[\mathrm{SO}_{4}^{2-}\right] \times(-2)^{2}\right\}} \\ {\mu=\frac{1}{2}\left\{(0.20) \times(+1)^{2}+(0.10) \times(-2)^{2}\right\}=0.30 \ \mathrm{M}}\end{array} \nonumber \]

Al calcular las fuerzas iónicas de estas soluciones estamos ignorando la presencia de H ₃ O ⁺ y OH ^—, y, en el caso de Na ₂ SO ₄, la presencia de la reacción\(\text{HSO}_4^-\) de disociación de base de\(\text{SO}_4^{2-}\). En el caso de NaCl 0.10 M, las concentraciones de H ₃ O ⁺ y OH ^—son\(1.0 \times 10^{-7}\), que es significativamente menor que las concentraciones de Na ⁺ y Cl ^—. Debido a que\(\text{SO}_4^{2-}\) es una base muy débil (K _b =\(1.0 \times 10^{-12}\)), la solución es sólo ligeramente básica (pH = 7.5), y las concentraciones de H ₃ O ⁺, OH ^—, y\(\text{HSO}_4^-\) son insignificantes. Aunque podemos ignorar la presencia de H ₃ O ⁺, OH ^—, y\(\text{HSO}_4^-\) cuando calculamos la fuerza iónica de estas dos soluciones, tenga en cuenta que una reacción de equilibrio puede generar iones que podrían afectar la fuerza iónica de la solución.

Tenga en cuenta que la unidad para la fuerza iónica es la molaridad, pero que la fuerza iónica de una sal no necesita coincidir con su concentración molar. Para una sal 1:1, como NaCl, la fuerza iónica y la concentración molar son idénticas. La fuerza iónica de un electrolito 2:1, como Na ₂ SO ₄, es tres veces mayor que la concentración molar del electrolito.

Coeficientes de actividad y actividad

La Figura 35.7.1 muestra que agregar KNO ₃ a una mezcla de Fe ^{3 +} y SCN ^— disminuye la constante de formación para Fe (SCN) ²⁺. Esto crea una contradicción. Anteriormente en este capítulo demostramos que existe una relación entre la energía libre de estado estándar de una reacción, ∆G ^o, y su constante de equilibrio, K.

\[\triangle G^{\circ}=-R T \ln K \nonumber \]

Debido a que una reacción tiene un solo estado estándar, su constante de equilibrio debe ser independiente de las condiciones de la solución. Aunque la fuerza iónica afecta la constante de formación aparente para Fe (SCN) ²⁺, la reacción\ ref {6.1} debe tener una constante de formación termodinámica subyacente que sea independiente de la fuerza iónica.

La constante de formación aparente para Fe (SCN) ²⁺, como se muestra en la Ecuación\ ref {6.2}, es una función de las concentraciones. En lugar de concentraciones, definimos la verdadera constante de equilibrio termodinámico utilizando actividades. La actividad de la especie A, a _A, es producto de su concentración, [A], y de un coeficiente de actividad dependiente de la solución,\(\gamma_A\)

\[a_{A}=[A] \gamma_{A} \nonumber \]

La verdadera constante de formación termodinámica para Fe (SCN) ²⁺, por lo tanto, es

\[K_{1}=\frac{a_{\mathrm{Fe}(S \mathrm{CN})^{2+}}}{a_{\mathrm{Fe}^{3+}} \times a_{\mathrm{SCN}^-}}=\frac{\left[\mathrm{Fe}(\mathrm{SCN})^{2+}\right] \gamma_{\mathrm{Fe}(\mathrm{SCN})^{2+}}}{\left[\mathrm{Fe}^{3+}\right] \gamma_{\mathrm{Fe}^{3+}}\left[\mathrm{SCN}^{-}\right] \gamma_{\mathrm{SCN}^{-}}} \nonumber \]

A menos que se especifique lo contrario, las constantes de equilibrio en los apéndices son constantes de equilibrio termodinámico.

El coeficiente de actividad de una especie corrige cualquier desviación entre su concentración física y su valor ideal. Para un gas, un sólido puro, un líquido puro o un soluto no iónico, el coeficiente de actividad es aproximadamente uno en las condiciones experimentales más razonables.

Para un gas los términos adecuados son fugacidad y coeficiente de fugacidad, en lugar de actividad y coeficiente de actividad.

Para una reacción que involucra únicamente a estas especies, la diferencia entre actividad y concentración es insignificante. El coeficiente de actividad para un ion, sin embargo, depende de la fuerza iónica de la solución, la carga del ion y el tamaño del ión. Es posible estimar coeficientes de actividad utilizando la ecuación extendida de Debye‐Hückel

\[\log \gamma_{A}=\frac{-0.51 \times z_{A}^{2} \times \sqrt{\mu}}{1+3.3 \times \alpha_{A} \times \sqrt{\mu}} \label{6.3} \]

donde z _A es la carga del ión,\(\alpha_A\) es el diámetro efectivo del ion hidratado en nanómetros (Tabla 6.2),\(\mu\) es la fuerza iónica de la solución, y 0.51 y 3.3 son constantes apropiadas para una solución acuosa a 25 ^o C. El radio efectivo del ion es el radio del ion más las moléculas de agua estrechamente unidas al ion. El radio efectivo es mayor para iones más pequeños y con mayor carga que para iones más grandes y con menos carga.

Tabla 35.7.1 . Diámetros efectivos (\(\alpha\)) para iones seleccionados

ion	diámetro efectivo (nm)
H 3 O ^+	0.9
Li ^+	0.6
Na ^+\(\text{IO}_3^-\),\(\text{HSO}_3^-\),\(\text{HCO}_3^-\),\(\text{H}_2\text{PO}_4^-\)	0.45
OH ^—, F ^—, SCN ^—, HS ^—\(\text{ClO}_3^-\),\(\text{ClO}_4^-\),\(\text{MnO}_4^-\)	0.35
K ^+, Cl ^—, Br ^—, I ^—, CN ^—\(\text{NO}_2^-\),\(\text{NO}_3^-\)	0.3
Cs ^+, Tl ^+, Ag ^+,\(\text{NH}_4^+\)	0.25
Mg ^2 ^+, Ser ^2+	0.8
Ca ^2 ^+, Cu ^2+, Zn ^2 ^+, Sn ^2+, Mn ^2 ^+, Fe ^2+, Ni ^2 ^+, Co ^2+	0.6
Sr ^2 ^+, Ba ^2+, Cd ^2+, Hg ^2+, S ^2—	0.5
Pb ^2+,\(\text{SO}_4^{2-}\),\(\text{SO}_3^{2-}\)	0.45
\(\text{Hg}_2^{2+}\),\(\text{SO}_4^{2-}\),\(\text{S}_22\text{O}_3^{2-}\),\(\text{CrO}_4^{2-}\),\(\text{HPO}_4^{2-}\)	0.40
Al ^3 ^+, Fe ^3+, Cr ^3 ^+	0.9
\(\text{PO}_4^{3-}\),\(\text{Fe(CN)}_6^{3-}\)	0.4
Zr ^4 ^+, Ce ^4+, Sn ^4 ^+	1.1
\(\text{Fe(CN)}_6^{4-}\)	0.5
Fuente: Kielland, J. J. Am. Chem. Soc. 1937, 59, 1675—1678.

Varias características de la Ecuación\ ref {6.3} merecen nuestra atención. Primero, a medida que la fuerza iónica se acerca a cero, el coeficiente de actividad de un ion se acerca a un valor de En una solución donde\(\mu = 0\), la actividad de un ión y su concentración son idénticas. Podemos aprovechar este hecho para determinar la constante de equilibrio termodinámico de una reacción midiendo la constante de equilibrio aparente para varias fuerzas iónicas cada vez más pequeñas y extrapolando de nuevo a una fuerza iónica de cero. Segundo, un coeficiente de actividad es menor, y el efecto de la actividad es más importante, para un ion con una carga más alta y un radio efectivo más pequeño. Finalmente, la ecuación extendida de Debye‐Hückel proporciona una estimación razonable del coeficiente de actividad de un ión cuando la fuerza iónica es menor a 0.1. Las modificaciones a la Ecuación\ ref {6.3} extienden el cálculo de los coeficientes de actividad a mayores fuerzas iónicas [Davies, C. W. Ion Association, Butterworth: London, 1962].

Incluir los coeficientes de actividad al resolver problemas de equilibrio

Anteriormente en este capítulo calculamos la solubilidad de Pb (IO ₃) ₂ en agua desionizada, obteniendo un resultado de\(4.0 \times 10^{-5}\) mol/L Debido a que la única fuente significativa de iones es de la reacción de solubilidad, la fuerza iónica es muy baja y podemos suponer que\(\gamma \approx 1\) para ambos Pb ^{2 +} y\(\text{IO}_3^-\). Al calcular la solubilidad de Pb (IO ₃) ₂ en agua desionizada, no es necesario tener en cuenta la fuerza iónica. Pero, ¿y si necesitamos conocer la solubilidad del Pb (IO ₃) ₂ en una solución que contenga otros iones inertes? En este caso necesitamos incluir coeficientes de actividad en nuestro cálculo.

Ejemplo 35.7.2

Calcular la solubilidad de Pb (IO ₃) ₂ en una matriz de 0.020 M Mg (NO ₃) ₂.

Solución

Comenzamos calculando la fuerza iónica de la solución. Dado que Pb (IO ₃) ₂ es escasamente soluble, asumiremos que podemos ignorar su contribución a la fuerza iónica; así

\[\mu=\frac{1}{2}\left\{(0.020)(+2)^{2}+(0.040)(-1)^{2}\right\}=0.060 \ \mathrm{M} \nonumber \]

A continuación, utilizamos la Ecuación\ ref {6.3} para calcular los coeficientes de actividad para Pb ²⁺ y\(\text{IO}_3^-\).

\[\log \gamma_{\mathrm{Pb}^{2+}}=\frac{-0.51 \times(+2)^{2} \times \sqrt{0.060}}{1+3.3 \times 0.45 \times \sqrt{0.060}}=-0.366 \nonumber \]

\[\gamma_{\mathrm{Pb}^{2+}}=0.431 \nonumber \]

\[\log \gamma_{\mathrm{IO}_{3}^{-}}=\frac{-0.51 \times(-1)^{2} \times \sqrt{0.060}}{1+3.3 \times 0.45 \times \sqrt{0.060}}=-0.0916 \nonumber \]

\[\gamma_{\mathrm{IO}_{3}^-}=0.810 \nonumber \]

Definir las concentraciones de equilibrio de Pb ^{2 +} y\(\text{IO}_3^-\) en términos de la variable x

Concentraciones	Pb (IO 3) 2 (s)	\(\rightleftharpoons\)	Pb ^2 ^+ (aq)	+	2\(\text{IO}_3^-\) (aq)
inicial	sólido		0		0
cambiar	sólido		+ x		+2 x
equilibrio	sólido		x		2 x

y sustituyendo en el producto de solubilidad termodinámica por Pb (IO ₃) ₂ nos deja con

\[K_{\mathrm{sp}}=a_{\mathrm{Pb}^{2+}} \times a_{\mathrm{IO}_{3}^-}^{2}=\gamma_{\mathrm{Pb}^{2+}}\left[\mathrm{Pb}^{2+}\right] \times \gamma_{\mathrm{IO}_3^-}^{2}\left[\mathrm{IO}_{3}^{-}\right]^{2}=2.5 \times 10^{-13} \nonumber \]

\[K_{\mathrm{sp}}=(0.431)(x)(0.810)^{2}(2 x)^{2}=2.5 \times 10^{-13} \nonumber \]

\[K_{\mathrm{sp}}=1.131 x^{3}=2.5 \times 10^{-13} \nonumber \]

Resolviendo para x da\(6.0 \times 10^{-5}\) y una solubilidad molar de\(6.0 \times 10^{-5}\) mol/L para Pb (IO ₃) ₂. Si ignoramos la actividad, como hicimos en nuestro cálculo anterior, reportamos la solubilidad molar como\(4.0 \times 10^{-5}\) mol/L, y al no tener en cuenta la actividad en este caso se subestima la solubilidad molar de Pb (IO ₃) ₂ en 33%.

La composición de equilibrio de la solución es

\[\begin{array}{c}{\left[\mathrm{Pb}^{2+}\right]=6.0 \times 10^{-5} \ \mathrm{M}} \\ {\left[\mathrm{IO}_{3}^{-}\right]=1.2 \times 10^{-4} \ \mathrm{M}} \\ {\left[\mathrm{Mg}^{2+}\right]=0.020 \ \mathrm{M}} \\ {\left[\mathrm{NO}_{3}^{-}\right]=0.040 \ \mathrm{M}}\end{array} \nonumber \]

Debido a que las concentraciones tanto de Pb ^{2 +} como\(\text{IO}_3^-\) son mucho menores que las concentraciones de Mg ^{2 +} y\(\text{NO}_3^-\) nuestra decisión de ignorar la contribución de Pb ^{2 +} y\(\text{IO}_3^-\) a la fuerza iónica es razonable.

Cómo manejamos el cálculo si no podemos ignorar las concentraciones de Pb ^{2 +} y\(\text{IO}_3^-\) al calcular la fuerza iónica. Un enfoque es utilizar el método de aproximaciones sucesivas. Primero, recalculamos la fuerza iónica usando las concentraciones de todos los iones, incluyendo Pb ^{2 +} y\(\text{IO}_3^-\). A continuación, recalculamos los coeficientes de actividad para Pb ^{2 +} y\(\text{IO}_3^-\) usando esta nueva fuerza iónica y luego recalculamos la solubilidad molar. Continuamos este ciclo hasta que dos cálculos sucesivos arrojan la misma solubilidad molar dentro de un margen de error aceptable.

Ejercicio 35.7.1

Calcular la solubilidad molar de Hg ₂ Cl ₂ en NaCl 0.10 M, tomando en cuenta el efecto de la fuerza iónica. Compara tu respuesta con la del Ejercicio 6.7.2 en el que ignoraste el efecto de la fuerza iónica.

Responder

Comenzamos calculando la fuerza iónica de la solución. Debido a que el NaCl es una sal iónica 1:1, la fuerza iónica es la misma que la concentración de NaCl; así\(\mu\) = 0.10 M. Esto supone, por supuesto, que podemos ignorar las contribuciones de\(\text{Hg}_2^{2+}\) y Cl ^—de la solubilidad de Hg ₂ Cl ₂.

A continuación usamos la Ecuación\ ref {6.3} para calcular los coeficientes de actividad para\(\text{Hg}_2^{2+}\) y Cl ^—.

\[\log \gamma_{\mathrm{Hg}_{2}^{2+}}=\frac{-0.51 \times(+2)^{2} \times \sqrt{0.10}}{1+3.3 \times 0.40 \times \sqrt{0.10}}=-0.455 \nonumber \]

\[\gamma_{\mathrm{H} \mathrm{g}_{2}^{2+}}=0.351 \nonumber \]

\[\log \gamma_{\mathrm{Cl}^{-}}=\frac{-0.51 \times(-1)^{2} \times \sqrt{0.10}}{1+3.3 \times 0.3 \times \sqrt{0.10}}=-0.12 \nonumber \]

\[\gamma_{\mathrm{Cl}^-}=0.75 \nonumber \]

Definir las concentraciones de equilibrio de\(\text{Hg}_2^{2+}\) y Cl ^— en términos de la variable x

concentraciones	Hg2Cl2 (s)	\(\rightleftharpoons\)	\(\text{Hg}_2^{2+}\)(aq)	+	2Cl ^— (aq)
inicial	sólido		0		0.10
cambiar	sólido		+ x		+2 x
equilibrio	sólido		x		0.10 + 2 x

y sustituyendo en el producto de solubilidad termodinámica Hg ₂ Cl ₂, déjanos con

\[K_{\mathrm{sp}}=a_{\mathrm{Hg}_{2}^{2+}}\left(a_{\mathrm{Cl}^-}\right)^{2} = \gamma_{\mathrm{Hg}_{2}^{2+}}\left[\mathrm{Hg}_{2}^{2+}\right]\left(\gamma_{\mathrm{Cl}^{-}}\right)^{2}\left[\mathrm{Cl}^{-}\right]^{2}=1.2 \times 10^{-18} \nonumber \]

Debido a que el valor de x probable es pequeño, simplifiquemos esta ecuación para

\[(0.351)(x)(0.75)^{2}(0.1)^{2}=1.2 \times 10^{-18} \nonumber \]

Resolviendo para x da su valor como\(6.1 \times 10^{-16}\). ^{Debido a que x es la concentración de\(\text{Hg}_2^{2+}\) y 2 x es la concentración de Cl, nuestra decisión de ignorar sus contribuciones a la fuerza iónica es razonable.} La solubilidad molar de Hg ₂ Cl ₂ en NaCl 0.10 M es\(6.1 \times 10^{-16}\) mol/L. En el Ejercicio 6.7.2, donde ignoramos la fuerza iónica, determinamos que la solubilidad molar de Hg ₂ Cl ₂ es\(1.2 \times 10^{-16}\) mol/L, resultado que es\(5 \times\) menor que el su valor real.

Como muestran el Ejemplo 35.7.2 y Ejercicio 35.7.1 , no corregir el efecto de la fuerza iónica puede conducir a un error significativo en un cálculo de equilibrio. Sin embargo, no es inusual ignorar las actividades y suponer que la constante de equilibrio se expresa en términos de concentraciones. Hay una razón práctica para ello: en un análisis rara vez conocemos la composición exacta, mucho menos la fuerza iónica de muestras acuosas o de muestras sólidas puestas en solución. Los cálculos de equilibrio son una guía útil cuando desarrollamos un método analítico; sin embargo, solo es cuando completamos un análisis y evaluamos los resultados que podemos juzgar si nuestra teoría coincide con la realidad. Al final, el trabajo en el laboratorio es el paso más crítico para desarrollar un método analítico confiable.

Este es un buen lugar para revisitar el significado del pH. En el Capítulo 2 definimos el pH como

\[\mathrm{pH}=-\log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right] \nonumber \]

Ahora vemos que la definición correcta es

\[\begin{array}{c}{\mathrm{pH}=-\log a_{\mathrm{H}_{3} \mathrm{O}^{+}}} \\ {\mathrm{pH}=-\log \gamma_{\mathrm{H}_{3} \mathrm{O}^{+}}\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}\end{array} \nonumber \]

No tener en cuenta el efecto de la fuerza iónica puede conducir a un error significativo en la concentración reportada de H ₃ O ⁺. Por ejemplo, si el pH de una solución es 7.00 y el coeficiente de actividad para H ₃ O ⁺ es 0.90, entonces la concentración de H ₃ O ⁺ es\(1.11 \times 10^{-7}\) M, no\(1.00 \times 10^{-7}\) M, un error de +11%. Afortunadamente, cuando desarrollamos y realizamos un método analítico, estamos más interesados en controlar el pH que en calcular [H ₃ O ⁺]. Como resultado, la diferencia entre las dos definiciones de pH rara vez es de gran preocupación.