4.1: Formas de Resumir Datos

En el Capítulo 3 se utilizaron datos recopilados de 30 bolsas de M&Ms para explorar diferentes formas de visualizar datos. En este capítulo consideramos varias formas de resumir datos utilizando los pesos netos de las mismas bolsas de M&Ms. Aquí están los datos brutos.

Mesa\(\PageIndex{1}\): Pesos Netos para 30 Bolsas de M&Ms.

49.287	48.870	51.250	48.692	48.777	46.405
49.693	49.391	48.196	47.326	50.974	50.081
47.841	48.377	47.004	50.037	48.599	48.625
48.395	51.730	50.405	47.305	49.477	48.027
48.212	51.682	50.802	49.055	46.577	48.317

Sin completar ningún cálculo, ¿qué conclusiones podemos sacar con solo mirar estos datos? Aquí hay algunos:

• Todos los pesos netos son mayores a 46 g y menores a 52 g.
• Como vemos en la Figura\(\PageIndex{1}\), una gráfica de caja y bigotes (superpuesta con un stripchart) y un histograma sugieren que la distribución de los pesos netos es razonablemente simétrica.
• La ausencia de puntos más allá de los bigotes de la trama de caja y bigotes sugiere que no hay pesos netos inusualmente grandes o insualmente pequeños.

Figura\(\PageIndex{1}\): Dos visualizaciones de los pesos netos de paquetes de M&Ms.

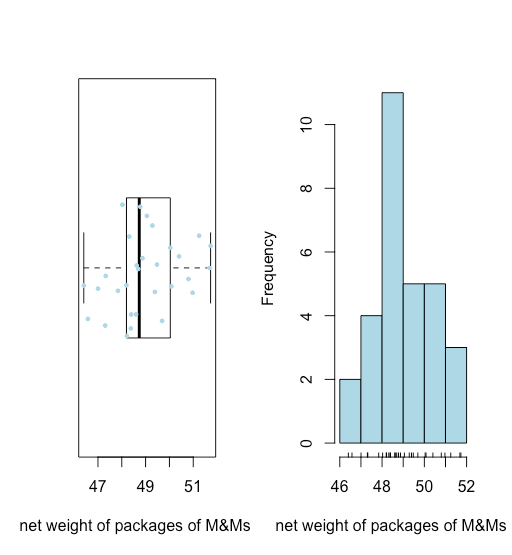
Ambas visualizaciones proporcionan una buena imagen cualitativa de los datos, sugiriendo que los resultados individuales están dispersos alrededor de algún valor central con más resultados más cercanos a ese valor central que a distancia de él. Ninguna visualización, sin embargo, describe los datos cuantitativamente. Lo que necesitamos es una manera conveniente de resumir los datos informando dónde están centrados los datos y qué tan variados son los resultados individuales alrededor de ese centro.

¿Dónde está el Centro?

Hay dos formas comunes de reportar el centro de un conjunto de datos: la media y la mediana.

La media,\(\overline{Y}\), es la media numérica obtenida sumando los resultados para todas las n observaciones y dividiendo por el número de observaciones

\[\overline{Y} = \frac{ \sum_{i = 1}^n Y_{i} } {n} = \frac{49.287 + 48.870 + \cdots + 48.317} {30} = 48.980 \text{ g} \nonumber\]

La mediana,\(\widetilde{Y}\), es el valor medio después de ordenar nuestras observaciones de menor a mayor, como mostramos aquí para nuestros datos.

Cuadro\(\PageIndex{2}\): Los datos de la Tabla\(\PageIndex{1}\) Ordenada De Menor a Mayor en Valor.

46.405	46.577	47.004	47.305	47.326	47.841
48.027	48.196	48.212	48.317	48.377	48.395
48.599	48.625	48.692	48.777	48.870	49.055
49.287	49.391	49.477	49.693	50.037	50.081
50.405	50.802	50.974	51.250	51.682	51.730

Si tenemos un número impar de muestras, entonces la mediana es simplemente el valor medio, o

\[\widetilde{Y} = Y_{\frac{n + 1}{2}} \nonumber\]

donde n es el número de muestras. Si, como es el caso aquí, n es par, entonces

\[\widetilde{Y} = \frac {Y_{\frac{n}{2}} + Y_{\frac{n}{2}+1}} {2} = \frac {48.692 + 48.777}{2} = 48.734 \text{ g} \nonumber\]

Cuando nuestros datos tienen una distribución simétrica, como creemos que es el caso aquí, entonces la media y la mediana tendrán valores similares.

¿Cuál es la variación de los datos sobre el centro?

Hay cinco medidas comunes de la variación de datos sobre su centro: la varianza, la desviación estándar, el rango, el rango intercuartil y la diferencia media media.

La varianza, s ², es una desviación cuadrada promedio de las observaciones individuales en relación con la media

\[s^{2} = \frac { \sum_{i = 1}^n \big(Y_{i} - \overline{Y} \big)^{2} } {n - 1} = \frac { \big(49.287 - 48.980\big)^{2} + \cdots + \big(48.317 - 48.980\big)^{2} } {30 - 1} = 2.052 \nonumber\]

y la desviación estándar, s, es la raíz cuadrada de la varianza, lo que le da las mismas unidades que la media.

\[s = \sqrt{\frac { \sum_{i = 1}^n \big(Y_{i} - \overline{Y} \big)^{2} } {n - 1}} = \sqrt{\frac { \big(49.287 - 48.980\big)^{2} + \cdots + \big(48.317 - 48.980\big)^{2} } {30 - 1}} = 1.432 \nonumber\]

El rango, w, es la diferencia entre el valor más grande y el más pequeño en nuestro conjunto de datos.

\[w = 51.730 \text{ g} - 46.405 \text{ g} = 5.325 \text{ g} \nonumber\]

El rango intercuartil, IQR, es la diferencia entre la mediana del 25% inferior de las observaciones y la mediana del 25% superior de las observaciones; es decir, proporciona una medida del rango de valores que abarca el 50% medio de las observaciones. No existe una fórmula única y estándar para calcular el IQR, y diferentes algoritmos arrojan resultados ligeramente diferentes. Adoptaremos el algoritmo descrito aquí:

1. Divida el conjunto de datos ordenados por la mitad; si hay un número impar de valores, elimine la mediana del conjunto de datos completo. Para nuestros datos, la mitad inferior es

Cuadro\(\PageIndex{3}\): La mitad inferior de los datos en la Tabla\(\PageIndex{2}\).

46.405	46.577	47.004	47.305	47.326
47.841	48.027	48.196	48.212	48.317
48.377	48.395	48.599	48.625	48.692

y la mitad superior es

Cuadro\(\PageIndex{4}\): La mitad superior de los datos en la Tabla\(\PageIndex{2}\).

48.777	48.870	49.055	49.287	49.391
49.477	49.693	50.037	50.081	50.405
50.802	50.974	51.250	51.682	51.730

2. Encuentra F _L, la mediana para la mitad inferior de los datos, que para nuestros datos es de 48.196 g.

3. Encuentra F _U, la mediana para la mitad superior de los datos, que para nuestros datos es 50.037 g.

4. El IQR es la diferencia entre F _U y F _L.

\[F_{U} - F_{L} = 50.037 \text{ g} - 48.196 \text{ g} = 1.841 \text{ g} \nonumber\]

La mediana de la desviación absoluta, MAD, es la mediana de las desviaciones absolutas de cada observación con respecto a la mediana de todas las observaciones. Para encontrar el MAD para nuestro conjunto de 30 pesos netos, primero restamos la mediana de cada muestra en la Tabla\(\PageIndex{1}\).

Cuadro\(\PageIndex{5}\): Los resultados de restar la mediana de cada valor en la tabla\(\PageIndex{1}\).

0.5525	0.1355	2.5155	-0.0425	0.0425	-2.3295
0.9585	0.6565	-0.5385	-1.4085	2.2395	1.3465
-0.8935	-0.3575	-1.7305	1.3025	-0.1355	-0.1095
-0.3395	2.9955	1.6705	-1.4295	0.7425	-0.7075
-0.5225	2.9475	2.0675	0.3205	-2.1575	-0.4175

A continuación tomamos el valor absoluto de cada diferencia y las clasificamos de menor a mayor.

Cuadro\(\PageIndex{6}\): Los Datos en la Tabla\(\PageIndex{5}\) Después de Tomar el Valor Absoluto.

0.0425	0.0425	0.1095	0.1355	0.1355	0.3205
0.3395	0.3575	0.4175	0.5225	0.5385	0.5525
0.6565	0.7075	0.7425	0.8935	0.9585	1.3025
1.3465	1.4085	1.4295	1.6705	1.7305	2.0675
2.1575	2.2395	2.3295	2.5155	2.9475	2.9955

Finalmente, reportamos la mediana para estos valores ordenados como

\[\frac{0.7425 + 0.8935}{2} = 0.818 \nonumber \]

Medidas robustas vs. no robustas del centro y variación sobre el centro

Una buena pregunta para hacer es por qué podríamos desear más de una forma de reportar el centro de nuestros datos y la variación en nuestros datos sobre el centro. Supongamos que el resultado para la última de nuestras 30 muestras se reportó como 483.17 en lugar de 48.317. Que se trate de un desplazamiento accidental del punto decimal o de un resultado verdadero no nos es relevante aquí; lo que importa es su efecto sobre lo que informamos. Aquí un resumen del efecto de este valor en cada una de nuestras formas de resumir nuestros datos.

Cuadro\(\PageIndex{7}\): Efecto sobre las estadísticas resumidas del cambio del último valor en la Tabla\(\PageIndex{1}\) De 48.317 g a 483.17 g.

estadística	datos originales	nuevos datos
media	48.980	63.475
mediana	48.734	48.824
varianza	2.052	6285.938
desviación estándar	1.433	79.280
gama	5.325	436.765
IQR	1.841	1.885
MAD	0.818	0.926

Tenga en cuenta que la media, la varianza, la desviación estándar y el rango son muy sensibles al cambio en el último resultado, pero la mediana, el IQR y el MAD no lo son. La mediana, el IQR y el MAD se consideran estadísticas robustas porque son menos sensibles a un resultado inusual; los otros son, por supuesto, estadísticas no robustas. Ambos tipos de estadísticas tienen valor para nosotros, un punto al que volveremos de vez en cuando.