7.1: Pruebas de significancia

Consideremos el siguiente problema. Para determinar si un medicamento es efectivo para disminuir las concentraciones de glucosa en sangre, recolectamos dos conjuntos de muestras de sangre de un paciente. Recolectamos un conjunto de muestras inmediatamente antes de administrar el medicamento, y recolectamos el segundo conjunto de muestras varias horas después. Después de analizar las muestras, reportamos sus respectivas medias y varianzas. ¿Cómo decidimos si el medicamento logró disminuir la concentración de glucosa en sangre del paciente?

Una forma de responder a esta pregunta es construir una curva de distribución normal para cada muestra y comparar las dos curvas entre sí. En la Figura se muestran tres posibles resultados\(\PageIndex{1}\). En la Figura\(\PageIndex{1a}\), hay una separación completa de las dos curvas de distribución normal, lo que sugiere que las dos muestras son significativamente diferentes entre sí. En la Figura\(\PageIndex{1b}\), las curvas de distribución normal para las dos muestras se superponen casi completamente entre sí, lo que sugiere que la diferencia entre las muestras es insignificante. La figura\(\PageIndex{1c}\), sin embargo, nos presenta un dilema. Aunque las medias para las dos muestras parecen diferentes, el solapamiento de sus curvas de distribución normal sugiere que un número significativo de posibles resultados podrían pertenecer a cualquiera de las dos distribuciones. En este caso lo mejor que podemos hacer es hacer una declaración sobre la probabilidad de que las muestras sean significativamente diferentes entre sí.

Figura\(\PageIndex{1}\): Tres ejemplos de las posibles relaciones entre las curvas de distribución normal para dos muestras. En (a) las curvas no se superponen, lo que sugiere que las muestras son significativamente diferentes entre sí. En (b) las dos curvas son casi idénticas, lo que sugiere que las muestras son indistinguibles. El solapamiento parcial de las curvas en (c) significa que lo mejor que podemos hacer es evaluar la probabilidad de que haya una diferencia entre las muestras.

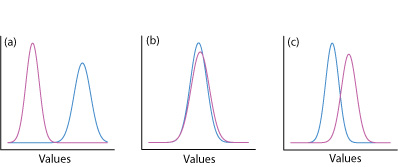
El proceso mediante el cual determinamos la probabilidad de que haya una diferencia significativa entre dos muestras se denomina prueba de significancia o prueba de hipótesis. Antes de discutir ejemplos específicos, primero establezcamos un enfoque general para la realización e interpretación de una prueba de significación.

Construyendo una prueba de significancia

El propósito de una prueba de significancia es determinar si la diferencia entre dos o más resultados es lo suficientemente grande como para que estemos cómodos afirmando que la diferencia no puede explicarse por errores indeterminados. El primer paso para construir una prueba de significancia es plantear el problema como una pregunta de sí o no, como

“¿Este medicamento es efectivo para bajar los niveles de glucosa en sangre de un paciente?”

Una hipótesis nula y una hipótesis alternativa definen las dos posibles respuestas a nuestra pregunta de sí o no. La hipótesis nula, H ₀, es que los errores indeterminados son suficientes para explicar cualquier diferencia entre nuestros resultados. La hipótesis alternativa, H _A, es que las diferencias en nuestros resultados son demasiado grandes para ser explicadas por error aleatorio y que deben ser determinadas en la naturaleza. Probamos la hipótesis nula, que o bien retenemos o rechazamos. Si rechazamos la hipótesis nula, entonces debemos aceptar la hipótesis alternativa y concluir que la diferencia es significativa.

No rechazar una hipótesis nula no es lo mismo que aceptarla. Conservamos una hipótesis nula porque no tenemos pruebas suficientes para demostrarla incorrecta. Es imposible probar que una hipótesis nula es cierta. Este es un punto importante y fácil de olvidar. Para apreciar este punto usemos estos datos para la masa de 100 centavos circulantes de Estados Unidos.

Mesa\(\PageIndex{1}\). Misas para una muestra de 100 centavos circulantes de Estados Unidos

Penny	Peso (g)	Penny	Peso (g)	Penny	Peso (g)	Penny	Peso (g)
1	3.126	26	3.073	51	3.101	76	3.086
2	3.140	27	3.084	52	3.049	77	3.123
3	3.092	28	3.148	53	3.082	78	3.115
4	3.095	29	3.047	54	3.142	79	3.055
5	3.080	30	3.121	55	3.082	80	3.057
6	3.065	31	3.116	56	3.066	81	3.097
7	3.117	32	3.005	57	3.128	82	3.066
8	3.034	33	3.115	58	3.112	83	3.113
9	3.126	34	3.103	59	3.085	84	3.102
10	3.057	35	3.086	60	3.086	85	3.033
11	3.053	36	3.103	61	3.084	86	3.112
12	3.099	37	3.049	62	3.104	87	3.103
13	3.065	38	2.998	63	3.107	88	3.198
14	3.059	39	3.063	64	3.093	89	3.103
15	3.068	40	3.055	65	3.126	90	3.126
16	3.060	41	3.181	66	3.138	91	3.111
17	3.078	42	3.108	67	3.131	92	3.126
18	3.125	43	3.114	68	3.120	93	3.052
19	3.090	44	3.121	69	3.100	94	3.113
20	3.100	45	3.105	70	3.099	95	3.085
21	3.055	46	3.078	71	3.097	96	3.117
22	3.105	47	3.147	72	3.091	97	3.142
23	3.063	48	3.104	73	3.077	98	3.031
24	3.083	49	3.146	74	3.178	99	3.083
25	3.065	50	3.095	75	3.054	100	3.104

Después de mirar los datos podríamos proponer las siguientes hipótesis nulas y alternativas.

H ₀: La masa de un centavo estadounidense circulante está entre 2.900 g y 3.200 g

H _A: La masa de un centavo circulante estadounidense puede ser inferior a 2.900 g o superior a 3.200 g

Para probar la hipótesis nula encontramos un centavo y determinamos su masa. Si la masa del centavo es de 2.512 g entonces podemos rechazar la hipótesis nula y aceptar la hipótesis alternativa. Supongamos que la masa del centavo es de 3.162 g. Aunque este resultado aumenta nuestra confianza en la hipótesis nula, no prueba que la hipótesis nula sea correcta porque el siguiente centavo que muestremos podría pesar menos de 2.900 g o más de 3.200 g.

Después de exponer las hipótesis nulas y alternativas, el segundo paso es elegir un nivel de confianza para el análisis. El nivel de confianza define la probabilidad de que rechacemos incorrectamente la hipótesis nula cuando es, de hecho, cierta. Podemos expresar esto como nuestra confianza en que tenemos razón al rechazar la hipótesis nula (e.g. 95%), o como la probabilidad de que seamos incorrectos al rechazar la hipótesis nula. Para este último, el nivel de confianza se da como\(\alpha\), donde

\[\alpha = 1 - \frac {\text{confidence interval (%)}} {100} \nonumber\]

Para un nivel de confianza del 95%,\(\alpha\) es 0.05.

El tercer paso consiste en calcular un estadístico de prueba apropiado y compararlo con un valor crítico. El valor crítico del estadístico de prueba define un punto de interrupción entre valores que nos llevan a rechazar o retener la hipótesis nula, que es el cuarto y último paso de una prueba de significancia. Como veremos en las secciones que siguen, la forma en que calculemos el estadístico de prueba depende de lo que estemos comparando.

Los cuatro pasos para un análisis estadístico de los datos mediante una prueba de significancia:

1. Plantar una pregunta, y exponer la hipótesis nula, H ₀, y la hipótesis alternativa, H _A.
2. Elija un nivel de confianza para el análisis estadístico.
3. Calcular un estadístico de prueba apropiado y compararlo con un valor crítico.
4. O bien conservar la hipótesis nula, o rechazarla y aceptar la hipótesis alternativa.

Pruebas de significancia de una cola y dos colas

Supongamos que queremos evaluar la precisión de un nuevo método analítico. Podríamos usar el método para analizar un Material de Referencia Estándar que contenga una concentración conocida de analito,\(\mu\). Analizamos el estándar varias veces, obteniendo un valor medio\(\overline{X}\), para la concentración del analito. Nuestra hipótesis nula es que no hay diferencia entre\(\overline{X}\) y\(\mu\)

\[H_0 \text{: } \overline{X} = \mu \nonumber\]

Si realizamos la prueba de significancia en\(\alpha = 0.05\), entonces conservamos la hipótesis nula si un intervalo de confianza del 95% alrededor\(\overline{X}\) contiene\(\mu\). Si la hipótesis alternativa es

\[H_\text{A} \text{: } \overline{X} \neq \mu \nonumber\]

entonces rechazamos la hipótesis nula y aceptamos la hipótesis alternativa si\(\mu\) se encuentra en las áreas sombreadas en cualquiera de los extremos de la curva de distribución de probabilidad de la muestra (Figura\(\PageIndex{2a}\)). Cada una de las áreas sombreadas representa 2.5% del área bajo la curva de distribución de probabilidad, para un total de 5%. Esta es una prueba de significancia de dos colas porque rechazamos la hipótesis nula para valores de ambos\(\mu\) extremos de la curva de distribución de probabilidad de la muestra.

Figura\(\PageIndex{2}\): Ejemplos de (a) prueba de significancia de dos colas y (b, c) de una cola de\(\overline{X}\) y\(\mu\). Las curvas de distribución de probabilidad, que son distribuciones normales, se basan en la media y desviación estándar de la muestra. Para\(\alpha\) = 0.05, las áreas azules representan el 5% del área bajo la curva. Si el valor de\(\mu\) cae dentro de las áreas azules, entonces rechazamos la hipótesis nula y aceptamos la hipótesis alternativa. Conservamos la hipótesis nula si el valor de\(\mu\) cae dentro del área no sombreada de la curva.

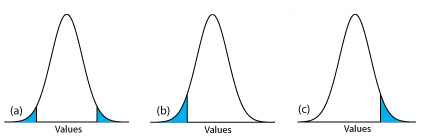
Podemos escribir la hipótesis alternativa de dos maneras adicionales

\[H_\text{A} \text{: } \overline{X} > \mu \nonumber\]

\[H_\text{A} \text{: } \overline{X} < \mu \nonumber\]

rechazando la hipótesis nula si\(\mu\) cae dentro de las áreas sombreadas que se muestran en la Figura\(\PageIndex{2b}\) o Figura\(\PageIndex{2c}\), respectivamente. En cada caso el área sombreada representa el 5% del área bajo la curva de distribución de probabilidad. Estos son ejemplos de una prueba de significancia de una cola.

Para un nivel de confianza fijo, una prueba de significancia de dos colas es la prueba más conservadora porque rechazar la hipótesis nula requiere una mayor diferencia entre los resultados que estamos comparando. En la mayoría de las situaciones no tenemos ninguna razón particular para esperar que un resultado debe ser mayor (o debe ser menor) que el otro resultado. Este es el caso, por ejemplo, cuando evaluamos la precisión de un nuevo método analítico. Una prueba de significancia de dos colas, por lo tanto, suele ser la elección adecuada.

Reservamos una prueba de significancia de una cola para una situación en la que específicamente estamos interesados en saber si un resultado es mayor (o menor) que el otro resultado. Por ejemplo, una prueba de significancia de una cola es apropiada si estamos evaluando la capacidad de un medicamento para disminuir los niveles de glucosa en sangre. En este caso solo nos interesa si los niveles de glucosa después de administrar el medicamento son menores que los niveles de glucosa antes de iniciar el tratamiento. Si el nivel de glucosa en sangre de un paciente es mayor después de administrar el medicamento, entonces conocemos la respuesta —la medicación no funcionó— y no necesitamos realizar un análisis estadístico.

Errores en las pruebas de significancia

Debido a que una prueba de significancia se basa en la probabilidad, su interpretación está sujeta a error. En una prueba de significancia,\(\alpha\) define la probabilidad de rechazar una hipótesis nula que es verdadera. Cuando realizamos una prueba de significancia en\(\alpha = 0.05\), hay un 5% de probabilidad de que rechacemos incorrectamente la hipótesis nula. Esto se conoce como error tipo 1, y su riesgo siempre es equivalente a\(\alpha\). Un error tipo 1 en una prueba de significancia de dos colas o una cola corresponde a las áreas sombreadas bajo las curvas de distribución de probabilidad en la Figura\(\PageIndex{2}\).

Un segundo tipo de error ocurre cuando conservamos una hipótesis nula aunque sea falsa. Este es un error tipo 2, y la probabilidad de que ocurra es\(\beta\). Desafortunadamente, en la mayoría de los casos no podemos calcular ni estimar el valor para\(\beta\). La probabilidad de un error tipo 2, sin embargo, es inversamente proporcional a la probabilidad de un error tipo 1.

Minimizar un error de tipo 1 al disminuir\(\alpha\) aumenta la probabilidad de un error de tipo 2. Cuando elegimos un valor para\(\alpha\) debemos comprometernos entre estos dos tipos de error. La mayoría de los ejemplos de este texto utilizan un nivel de confianza del 95% (\(\alpha = 0.05\)) porque esto suele ser un compromiso razonable entre los errores tipo 1 y tipo 2 para el trabajo analítico. No es inusual, sin embargo, utilizar un nivel de confianza más estricto (por ejemplo\(\alpha = 0.01\)) o más indulgente (por ejemplo\(\alpha = 0.10\)) cuando la situación lo requiere.