7.3: Análisis de varianza
- Page ID
- 69335
Considere los siguientes datos, que muestran la estabilidad de un reactivo bajo diferentes condiciones para almacenar muestras; todos los valores son recuperaciones porcentuales, por lo que un resultado de 100 indica que la concentración del reactivo permanece sin cambios y que no hubo degradación.
| pruebal/tratamiento | A (oscuridad total) | B (luz tenue) | C (luz completa) |
| 1 | 101 | 100 | 90 |
| 2 | 101 | 99 | 92 |
| 3 | 104 | 101 | 94 |
Para determinar si la luz tiene un efecto significativo en la estabilidad del reactivo, podríamos optar por realizar una serie de pruebas t, comparando todos los valores medios posibles; en este caso necesitamos tres pruebas de este tipo:
- comparar A a B
- comparar A a C
- Comparar B con C
Cada prueba de este tipo tiene una probabilidad de un error tipo I de\(\alpha_{test}\). La probabilidad total de un error tipo I a través de k pruebas,\(\alpha_{total}\), es
\[\alpha_{total} = 1 - (1 - \alpha_{test})^{k} \nonumber\]
Para tres pruebas de este tipo usando\(\alpha = 0.05\), tenemos
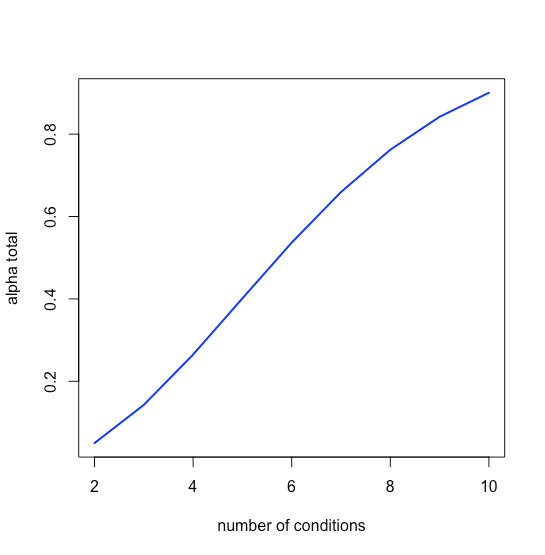
\[\alpha_{total} = 1 - (1 - 0.05)^{3} = 0.143 \nonumber\]
o una proabilidad del 14.3% de un error de tipo I. La relación entre el número de condiciones, n, y el número de pruebas, k, es
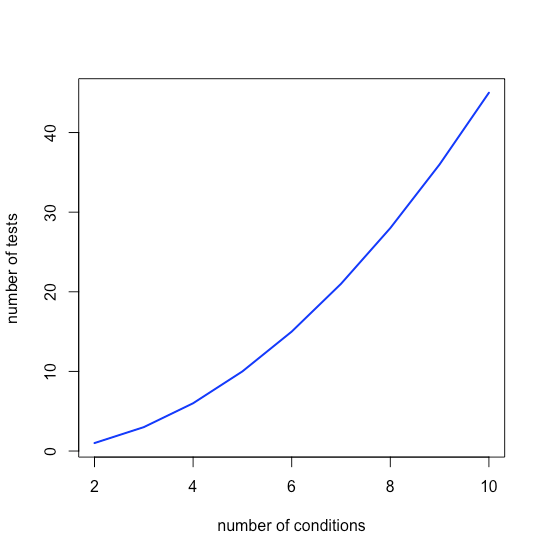
\[k = \frac {n(n-1)} {2} \nonumber\]
lo que significa que k crece rápidamente a medida que n aumenta, como se muestra en la Figura\(\PageIndex{1}\).
y que la magnitud de un error tipo I también aumenta rápidamente, como se ve en la Figura\(\PageIndex{2}\).
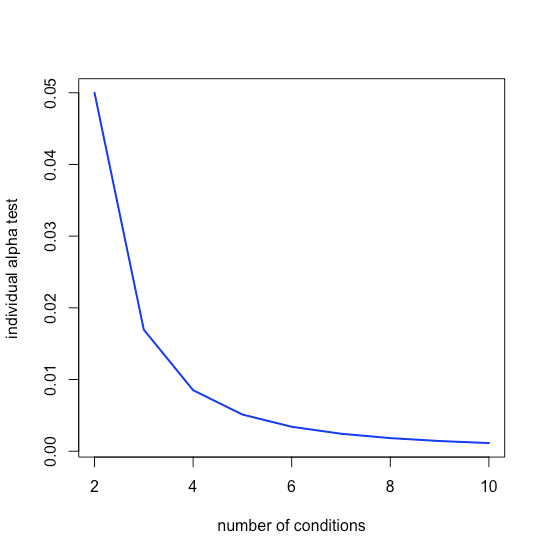
Podemos compensar este problema disminuyendo\(\alpha_{test}\) para cada prueba independiente de manera que\(\alpha_{total}\) sea igual a nuestra probabilidad deseada; así, para que\(n = 3\) tengamos\(k = 3\), y para lograr un\(\alpha_{total}\) de 0.05 cada valor individual de\(\alpha_{test}\) ser
\[\alpha_{test} = 1 - (1 - 0.05)^{1/3} = 0.017 \nonumber\]
Los valores de\(\alpha_{test}\) disminución rápida, como se ve en la Figura\(\PageIndex{3}\).
El problema aquí es que estamos buscando una diferencia significativa sobre una base de pares sin ninguna evidencia de que la variación general en los datos a través de todas las condiciones (también conocidas como tratamientos) es lo suficientemente grande como para que no pueda explicarse solo por la incertidumbre experimental (es decir, error aleatorio). Una forma de determinar si existe un error sistemático en el conjunto de datos, sin identificar la fuente del error sistemático, es comparar la variación dentro de cada tratamiento con la variación entre los tratamientos. Suponemos que la variación dentro de cada tratamiento refleja incertidumbre en el método analítico (errores aleatorios) y que la variación entre los tratamientos incluye tanto la incertidumbre del método como cualquier error sistemático en los tratamientos individuales. Si la variación entre los tratamientos es significativamente mayor que la variación dentro de los tratamientos, entonces parece probable un error sistemático. Llamamos a este proceso un análisis de varianza, o ANOVA; para una variable independiente (la cantidad de luz en este caso), es un análisis de varianza unidireccional.
Los detalles básicos de un cálculo ANOVA unidireccional son los siguientes:
Paso 1: Tratar los datos como un conjunto de datos grande y calcular su media y su varianza, que llamamos la media global,\(\bar{\bar{x}}\), y la varianza global,\(\bar{\bar{s^{2}}}\).
\[\bar{\bar{x}} = \frac { \sum_{i=1}^h \sum_{j=1}^{n_{i}} x_{ij} } {N} \nonumber\]
\[\bar{\bar{s^{2}}} = \frac { \sum_{i=1}^h \sum_{j=1}^{n_{i}} (x_{ij} - \bar{\bar{x}})^{2} } {N - 1} \nonumber\]
donde\(h\) es el número de tratamientos,\(n_{i}\) es el número de réplicas para el\(i^{th}\) tratamiento, y\(N\) es el número total de mediciones.
Paso 2: Calcular la varianza dentro de la muestra\(s_{w}^{2}\), utilizando la media para cada tratamiento\(\bar{x}_{i}\), y las réplicas para ese tratamiento.
\[s_{w}^{2} = \frac { \sum_{i=1}^h \sum_{j=1}^{n_{i}} (x_{ij} - \bar{x}_{i})^{2} } {N - h} \nonumber\]
Paso 3: Calcular la varianza entre muestras\(s_{b}^{2}\), utilizando las medias para cada tratamiento y la media global
\[s_{b}^{2} = \frac { \sum_{i=1}^h \sum_{j=1}^{n_{i}} (\bar{x}_{i} - \bar{\bar{x}})^2 } {h - 1} = \frac {\sum_{i=1}^h n_{i} (\bar{x}_{i} - \bar{\bar{x}})^2 } {h - 1} \nonumber\]
Paso 4: Si hay una diferencia significativa entre los tratamientos, entonces\(s_{b}^{2}\) debería ser significativamente mayor que\(s_{w}^{2}\), lo cual evaluamos usando una\(F\) prueba de una cola donde
\[H_{0}: s_{b}^{2} = s_{w}^{2} \nonumber\]
\[H_{A}: s_{b}^{2} > s_{w}^{2} \nonumber\]
Paso 5: Si hay una diferencia significativa, entonces estimamos\(\sigma_{rand}^{2}\) y\(\sigma_{systematic}^{2}\) como
\[s_{w}^{2} \approx \sigma_{rand}^{2} \nonumber\]
\[s_{b}^{2} \approx \sigma_{rand}^{2} + \bar{n}\sigma_{systematic}^{2} \nonumber\]
donde\(\bar{n}\) es el promedio de repeticiones por tratamiento.
Esto parece mucho trabajo, pero podemos simplificar los cálculos al señalar que
\[SS_{total} = \sum_{i=1}^h \sum_{j=1}^{n_{i}} (x_{ij} - \bar{\bar{x}})^{2} = \bar{\bar{s^{2}}}(N - 1) \nonumber\]
\[SS_{w} = \sum_{i=1}^h \sum_{j=1}^{n_{i}} (x_{ij} - \bar{x}_{i})^{2} \nonumber\]
\[SS_{b} = \sum_{i=1}^h n_{i} (\bar{x}_{i} - \bar{\bar{x}})^2 \nonumber\]
\[SS_{total} = SS_{w} + SS_{b} \nonumber\]
y eso\(SS_{total}\) y\(SS_{b}\) son relativamente fáciles de calcular, donde\(SS\) es corto para la suma de cuadrados. La tabla\(\PageIndex{1}\) reúne estas ecuaciones juntas
| fuente de varianza | suma de cuadrados | grados de libertad | varianza |
| entre muestras | \(\sum_{i=1}^h n_{i} (\bar{x}_{i} - \bar{\bar{x}})^2\) | \(h - 1\) | \(s_{b}^{2} = \frac {SS_{b}} {h - 1}\) |
| dentro de muestras | \(SS_{total} = SS_{w} + SS_{b}\) | \(N - h\) | \(s_{w}^{2} = \frac {SS_{w}} {N - h}\) |
| total | \(\bar{\bar{s^{2}}}(N - 1)\) |
Los reactivos químicos tienen una vida útil limitada. Para determinar el efecto de la luz sobre la estabilidad de un reactivo, una solución recién preparada se almacena durante una hora bajo tres condiciones de luz diferentes: oscuridad total, luz tenue y luz completa. Al cabo de una hora, cada solución se analizó tres veces, arrojando los siguientes porcentajes de recuperaciones; una recuperación del 100% significa que la concentración medida es la misma que la concentración real.La hipótesis nula es que no hay diferencia entre los diferentes tratamientos, y el hipótesis alternativa es que al menos uno de los tratamientos produce un resultado que es significativamente diferente al de los otros tratamientos.
| prueba/condición | A (oscuridad total) | B (luz tenue) | C (luz completa) |
| 1 | 101 | 100 | 90 |
| 2 | 101 | 99 | 92 |
| 3 | 104 | 101 | 94 |
Solución
Primero, tratamos los datos como un conjunto de datos grande de nueve valores y calculamos la media global\(\bar{\bar{x}}\), y la varianza global,\(\bar{\bar{s^{2}}}\); estos son 98 y 23.75, respectivamente. También se calcula la media para cada uno de los tres tratamientos, obteniendo un valor de 102.0 para el tratamiento A, 100.0 para el tratamiento B y 92.0 para el tratamiento C.
A continuación, calculamos la suma total de cuadrados,\(SS_{total}\)
\[\bar{\bar{s^{2}}}(N - 1) = 23.75(9 - 1) = 190.0 \nonumber\]
la suma de cuadrados entre muestras,\(SS_{b}\)
\[SS_{b} = \sum_{i=1}^h n_{i} (\bar{x}_{i} - \bar{\bar{x}})^2 = 3(102.0 - 98.0)^2 + 3(100.0 - 98.0)^2 + 3(92.0 - 98.0)^2 = 168.0 \nonumber\]
y la suma de cuadrados dentro de la muestra,\(SS_{w}\)
\[ SS_{w} = SS_{total} - SS_{b} = 190.0 - 168.0 = 22.0 \nonumber\]
La varianza entre los tratamientos,\(s_b^2\) es
\[\frac {SS_{b}} {h - 1} = \frac{168}{3 - 1} = 84.0 \nonumber\]
y la varianza dentro de los tratamientos,\(s_w^2\) es
\[\frac {SS_{w}} {N - h} = \frac{22.0}{9 - 3} = 3.67 \nonumber\]
Finalmente, completamos una prueba F, calculando F exp
\[F_{exp} = \frac{s_b^2}{s_w^2} = \frac{84.0}{3.67} = 22.9 \nonumber\]
y compararlo con el valor crítico para F (0.05, 2, 6) = 5.143 del Apéndice 3. Debido a que F exp > F (0.05, 2, 6), rechazamos la hipótesis nula y aceptamos la hipótesis alternativa de que al menos uno de los tratamientos produce un resultado que es significativamente diferente de los otros tratamientos. Podemos estimar la varianza debida a errores aleatorios como
\[\sigma_{random}^{2} = s_{w}^{2} = 3.67 \nonumber\]
y la varianza debida a errores sistemáticos como
\[\sigma_{systematic}^{2} = \frac {\sigma_{random}^{2} - s_{w}^{2}} {\bar{n}} = \frac {84.0 - 3.67} {3} = 26.8 \nonumber\]
Habiendo encontrado evidencia de una diferencia significativa entre los tratamientos, podemos usar pruebas t individuales en pares de tratamientos para mostrar que los resultados para el tratamiento C son significativamente diferentes de los otros dos tratamientos.


