11.3: Análisis de componentes principales

La siguiente figura, que es similar en estructura a la figura 11.2.2 pero con más muestras, muestra los valores de absorbancia para 80 muestras a longitudes de onda de 400.3 nm, 508.7 nm y 801.8 nm. Si bien los ejes definen el espacio en el que aparecen los puntos, los puntos individuales en sí mismos no están, con algunas excepciones, alineados con los ejes. La nube de 80 puntos tiene una posición media global dentro de este espacio y una varianza global alrededor de la media global (ver Capítulo 7.3 donde usamos estos términos en el contexto de un análisis de varianza).

Figura\(\PageIndex{1}\): Gráfica de dispersión que muestra los valores de absorbancia para 80 muestras a tres longitudes de onda: 400.3 nm, 508.7 nm y 801.8 nm. La Figura 11.2.2 muestra un subconjunto de estos datos utilizando 24 muestras de las 80 muestras.

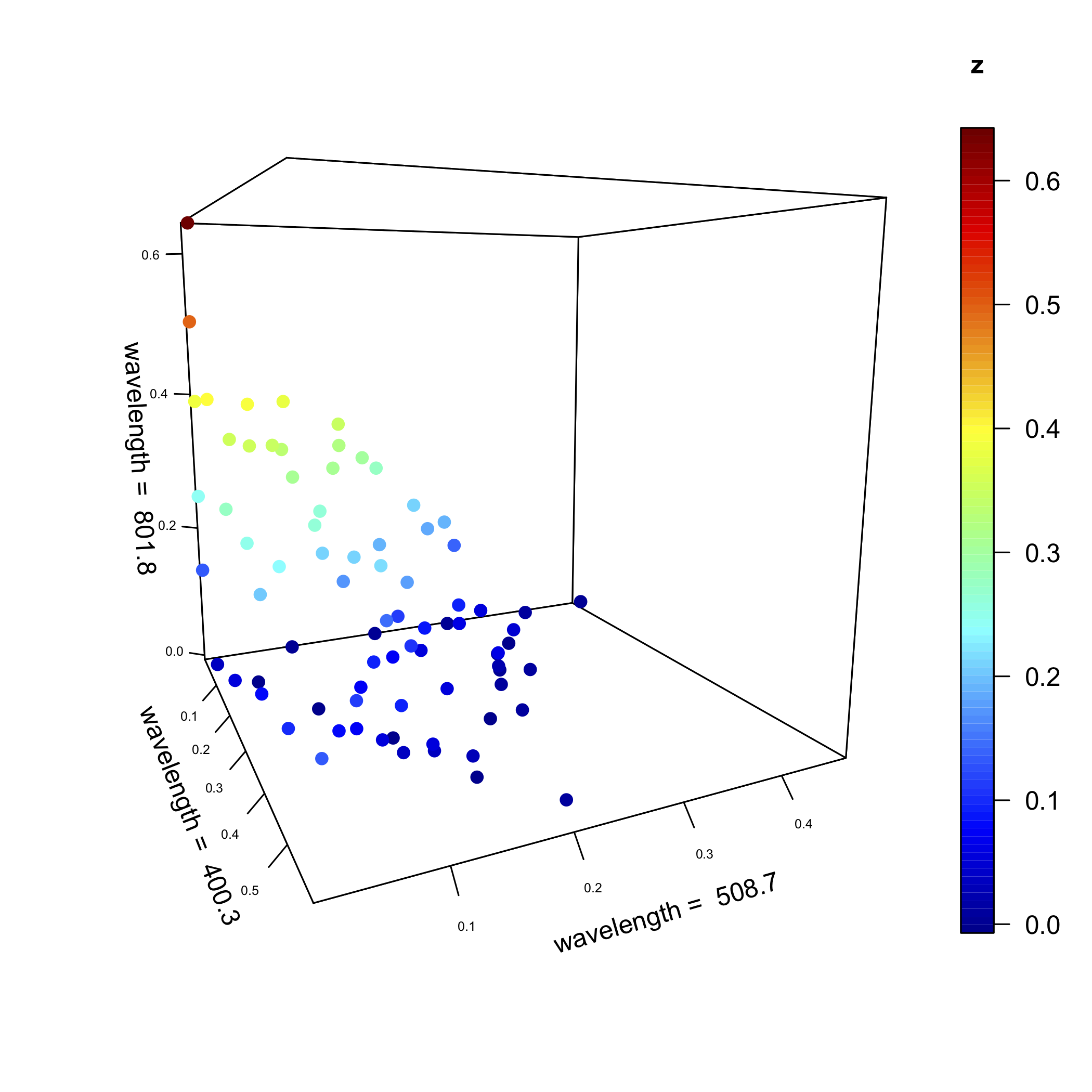
Supongamos que dejamos los puntos en el espacio como están y giramos los tres ejes. Podríamos rotar los tres ejes hasta que uno pase a través de la nube de manera que maximice la variación de los datos a lo largo de ese eje, lo que significa que este nuevo eje representa la mayor contribución a la varianza global. Habiendo alineado este eje primario con los datos, entonces lo mantenemos en su lugar y giramos los dos ejes restantes alrededor del eje primario hasta que uno de ellos pase a través de la nube de manera que maximice la varianza restante de los datos a lo largo de ese eje; este se convierte en el eje secundario. Finalmente, queda el tercer eje, o eje terciario, lo que explica cualquier varianza que quede. En esencia, esto es lo que comprende un análisis de componentes principales (ACP).

¿Cómo funciona un análisis de componentes principales?

Uno de los desafíos para entender cómo funciona PCA es que no podemos visualizar nuestros datos en más de tres dimensiones. Los datos de la Figura\(\PageIndex{1}\), por ejemplo, consisten en espectros para 24 muestras registradas a 635 longitudes de onda. ¡Para visualizar todos estos datos se requiere que los trazemos a lo largo de 635 ejes en el espacio de 635 dimensiones! Consideremos un sistema mucho más simple que consta de 21 muestras para cada una de las cuales medimos solo dos propiedades que llamaremos la primera variable y la segunda variable. La figura\(\PageIndex{2}\) muestra nuestros datos, los cuales podemos expresar como una matriz con 21 filas, una para cada una de las 21 muestras, y 2 columnas, una para cada una de las dos variables.

\[ [D]_{21 \times 2} \nonumber \]

Figura\(\PageIndex{2}\): El diagrama de dispersión de nuestras 21 muestras en función de sus valores para la primera variable y la segunda variable.

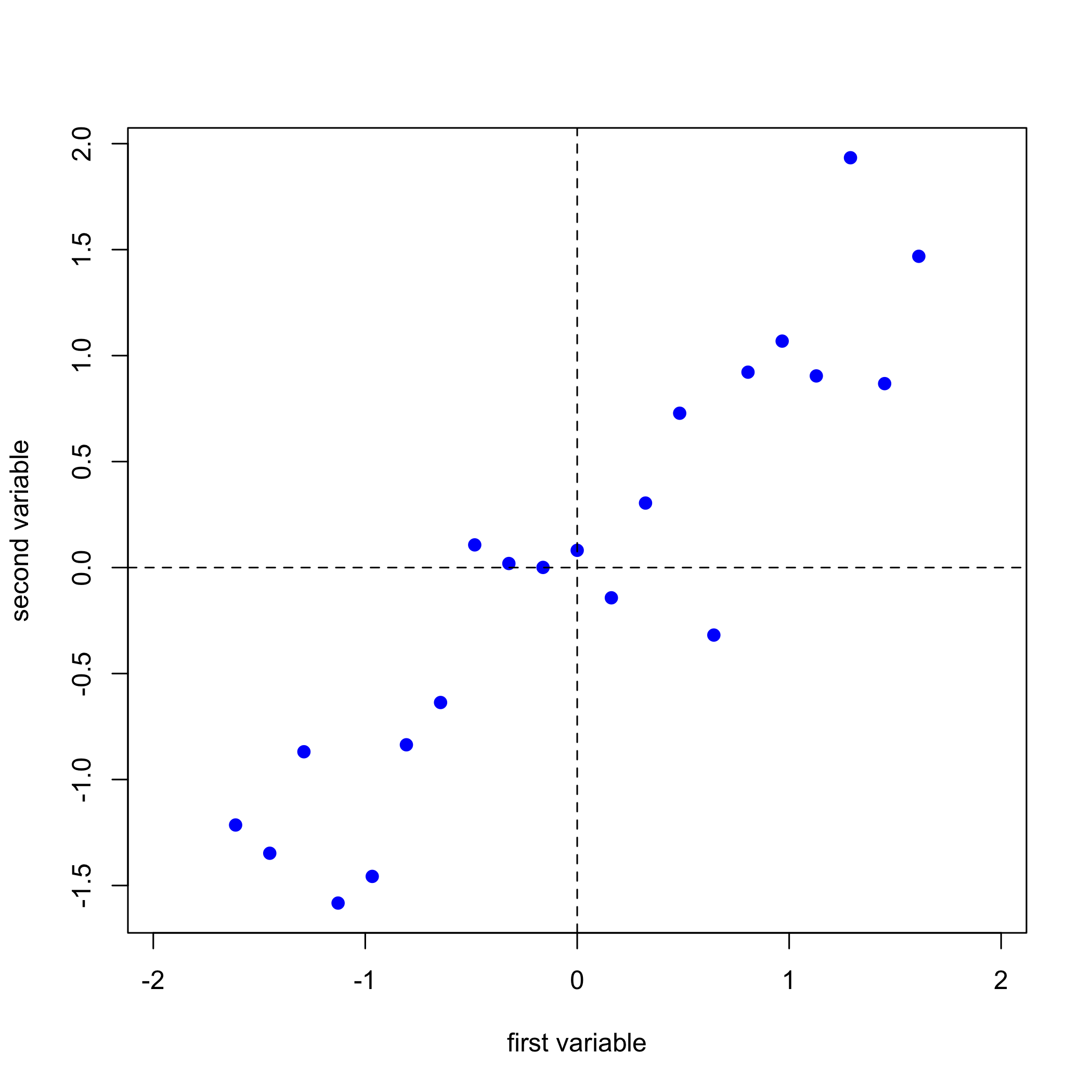
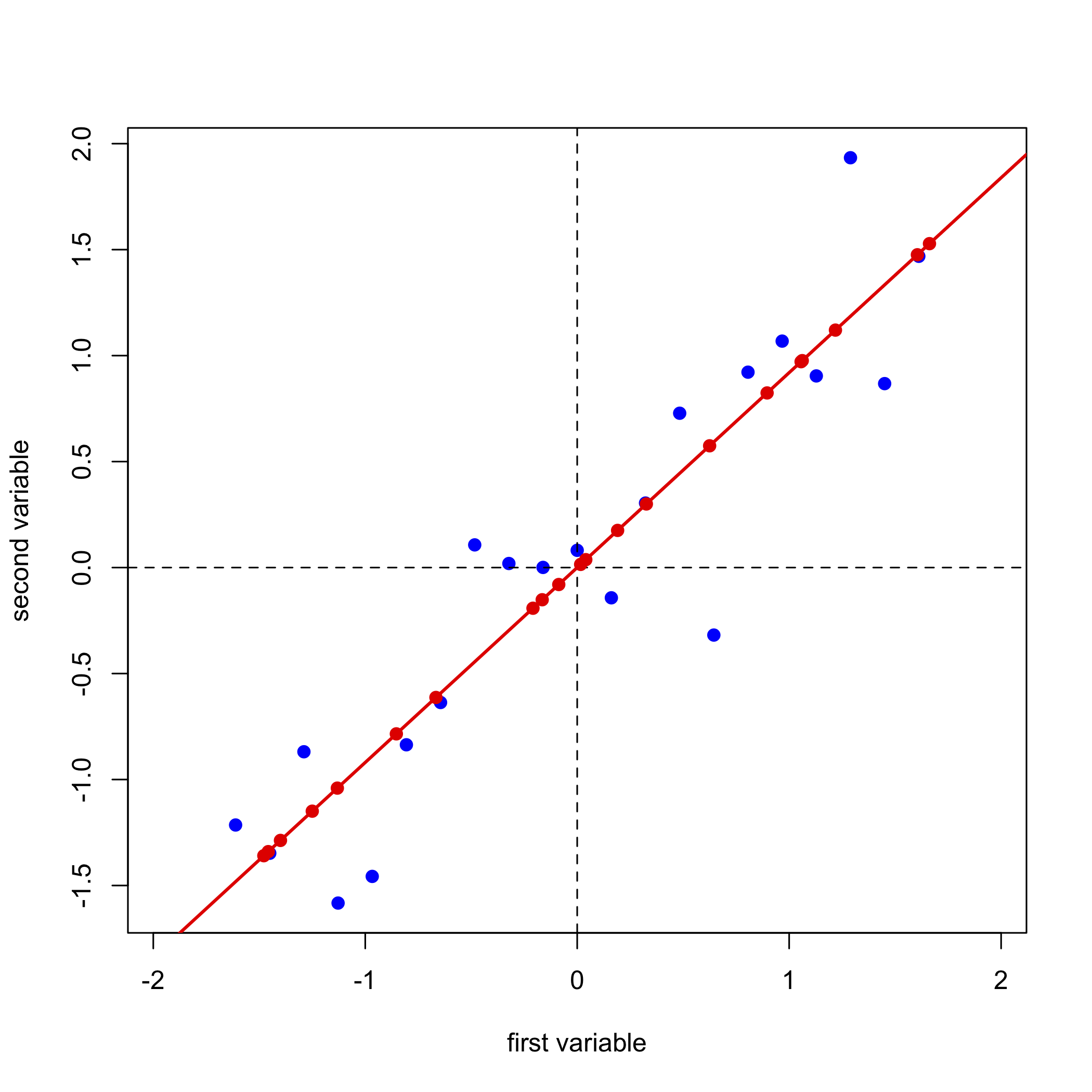
A continuación, completamos un análisis de regresión lineal sobre los datos y agregamos la línea de regresión a la gráfica; a esto lo llamamos el primer componente principal.

Figura\(\PageIndex{3}\): Los datos de la Figura\(\PageIndex{2}\) muestran la línea de regresión que es el primer eje del componente principal.

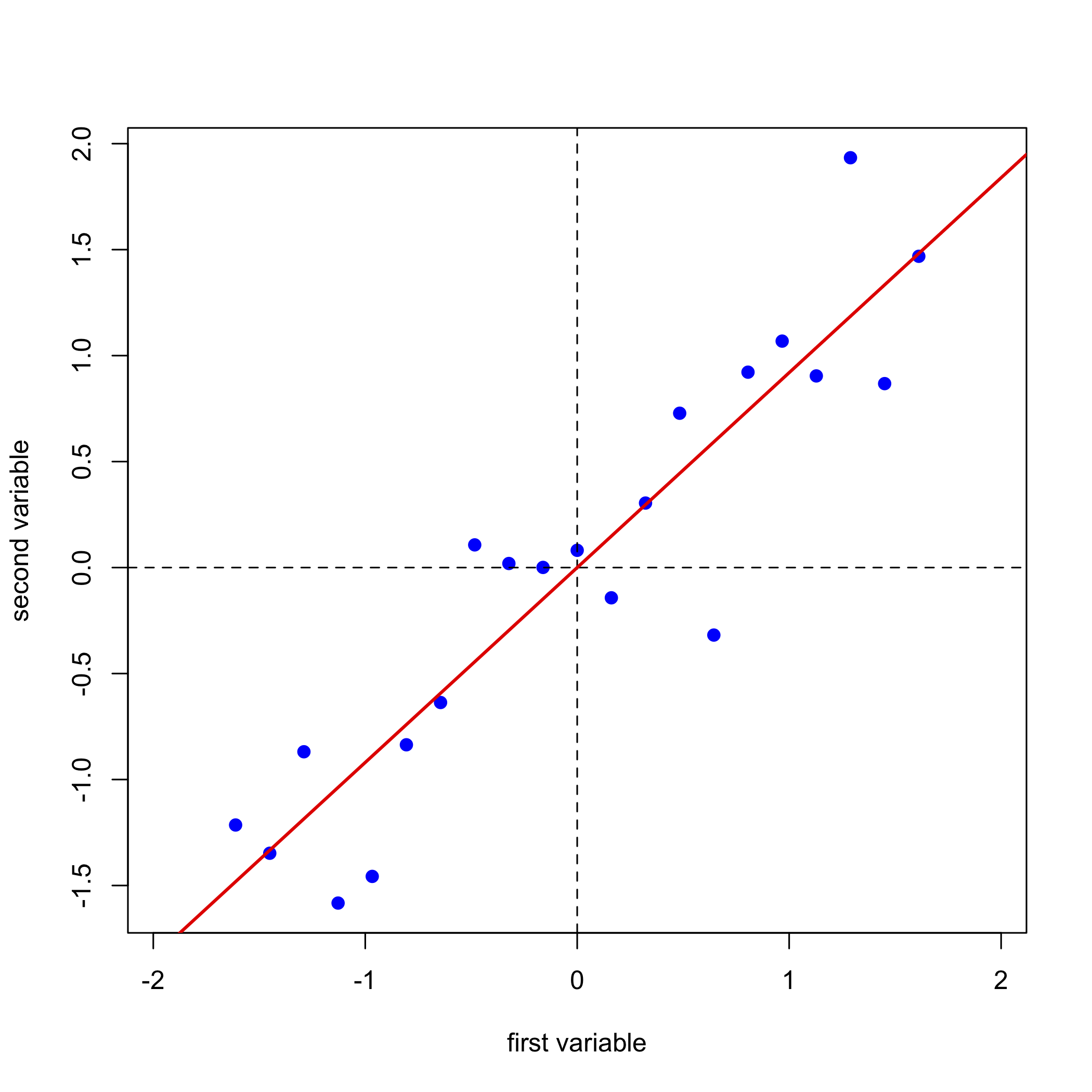
Proyectar nuestros datos (los puntos azules) sobre la línea de regresión (los puntos rojos) da la ubicación de cada punto en el eje del primer componente principal; estos valores se llaman las puntuaciones,\(S\). Los cosenos de los ángulos entre el eje del primer componente principal y los ejes originales se denominan cargas,\(L\). Podemos expresar la relación entre los datos, las puntuaciones y las cargas usando notación matricial. Obsérvese que a partir de las dimensiones de las matrices para\(D\)\(S\)\(L\),, y, cada una de las 21 muestras tiene una puntuación y cada una de las dos variables tiene una carga.

\[ [D]_{21 \times 2} = [S]_{21 \times 1} \times [L]_{1 \times 2} \nonumber\]

Figura\(\PageIndex{4}\): Las proyecciones (puntos rojos) sobre el primer eje componente principal de los datos originales (puntos azules) proporcionan las puntuaciones, que son una medida de la distancia de las proyecciones desde el origen.

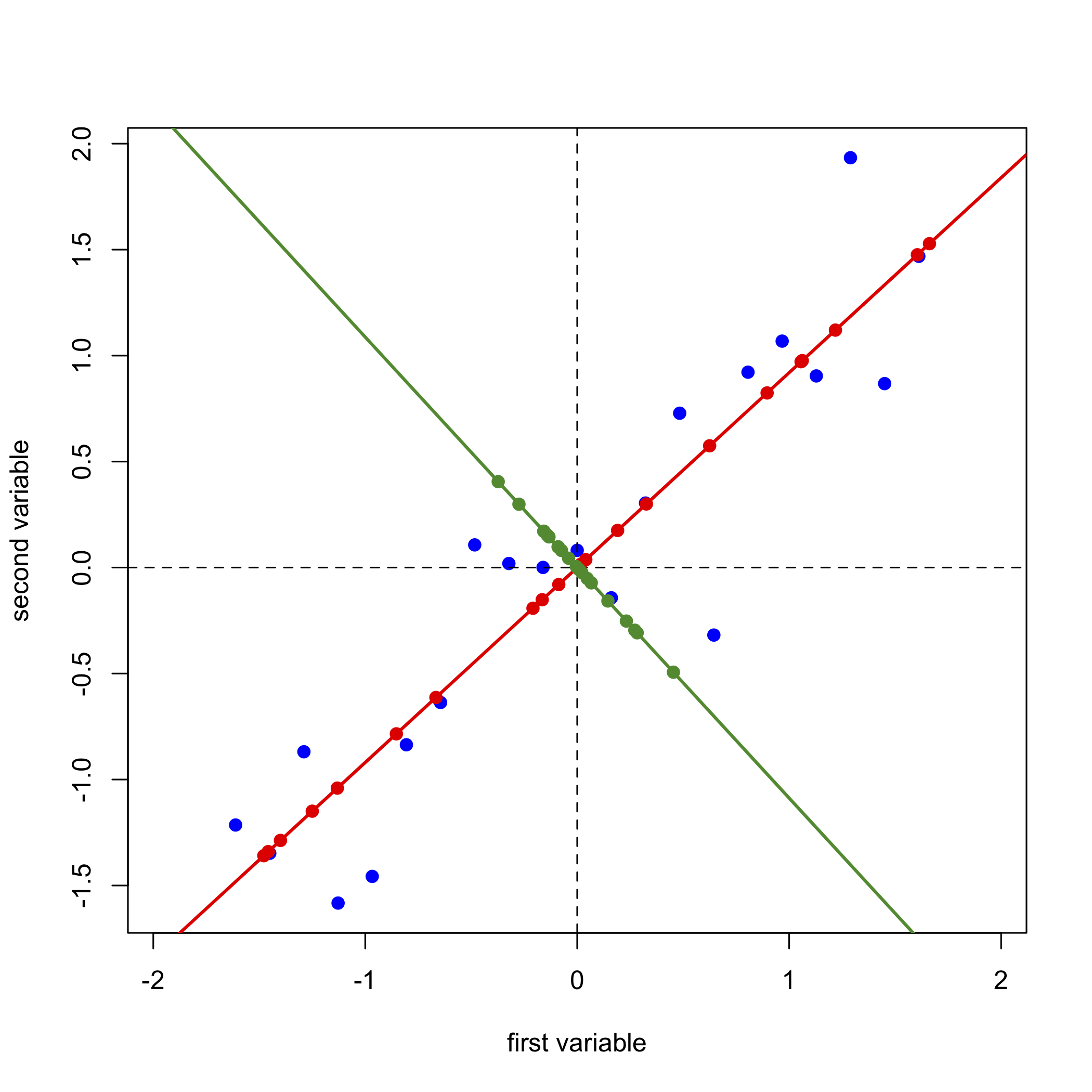
A continuación, dibujamos una línea perpendicular al primer eje del componente principal, que se convierte en el segundo (y último) eje del componente principal, proyectamos los datos originales sobre este eje (puntos en verde) y registramos las puntuaciones y cargas para el segundo componente principal.

\[ [D]_{21 \times 2} = [S]_{21 \times 2} \times [L]_{2 \times 2} \nonumber\]

Nota

En la multiplicación matricial el número de columnas en la primera matriz debe ser igual al número de filas de la segunda matriz. El resultado de la multiplicación matricial es una nueva matriz que tiene un número de filas igual al de la primera matriz y que tiene un número de columnas igual al de la segunda matriz; multiplicando así una matriz que está\(5 \times 4\) con una que es\(4 \times 8\) da una matriz que es\(5 \times 8\).

Figura\(\PageIndex{5}\): Las proyecciones (puntos verdes) de los datos originales (puntos azules) sobre el segundo y último eje del componente principal.

Si estuviéramos trabajando con 21 muestras y 10 variables, entonces haríamos esto:

1. trazar los datos para las 21 muestras en el espacio 10-dimensional donde cada variable es un eje
2. encontrar el eje del primer componente principal y tomar nota de las puntuaciones y cargas
3. proyectar los puntos de datos para las 21 muestras sobre la superficie de 9 dimensiones que es perpendicular al eje del primer componente principal
4. encontrar el eje del segundo componente principal y tomar nota de las puntuaciones y la carga
5. proyectar los puntos de datos para las 21 muestras sobre la superficie 8-dimensional que es perpendicular al segundo (y al primer) eje del componente principal
6. repetir hasta que se identifiquen los 10 componentes principales y se reporten todas las puntuaciones y cargas

¿Cómo interpretamos los resultados de un análisis de componentes principales?

Los resultados de un análisis de componentes principales están dados por las puntuaciones y las cargas. Volvamos a los datos de la Figura\(\PageIndex{1}\), pero para hacer las cosas más manejables, trabajaremos con solo 24 de las 80 muestras y ampliaremos el número de longitudes de onda de tres a 16 (un número que sigue siendo un pequeño subconjunto de las 635 longitudes de onda disponibles para nosotros). La siguiente figura muestra los espectros completos para estas 24 muestras y las longitudes de onda específicas que usaremos como líneas punteadas; así, nuestros datos son una matriz con 24 filas y 16 columnas,\([D]_{24 \times 16}\). Un análisis de componentes principales de estos datos arrojará 16 ejes de componentes principales.

Figura\(\PageIndex{6}\): Los espectros para 24 muestras. Las líneas punteadas mostraron las 16 longitudes de onda individuales, las cuales son 380.5 nm, 414.9 nm, 449.3 nm, 483.7 nm, 517.9 nm, 5506 nm, 538,2 nm, 613.3 nm, 642.9 nm, 672.7 nm, 703.3 nm, 735.5 nm, 767.8 nm, 800.2 nm, 832.6 nm y 868.6 nm. Se trata de los mismos datos utilizados para ilustrar el análisis de conglomerados.

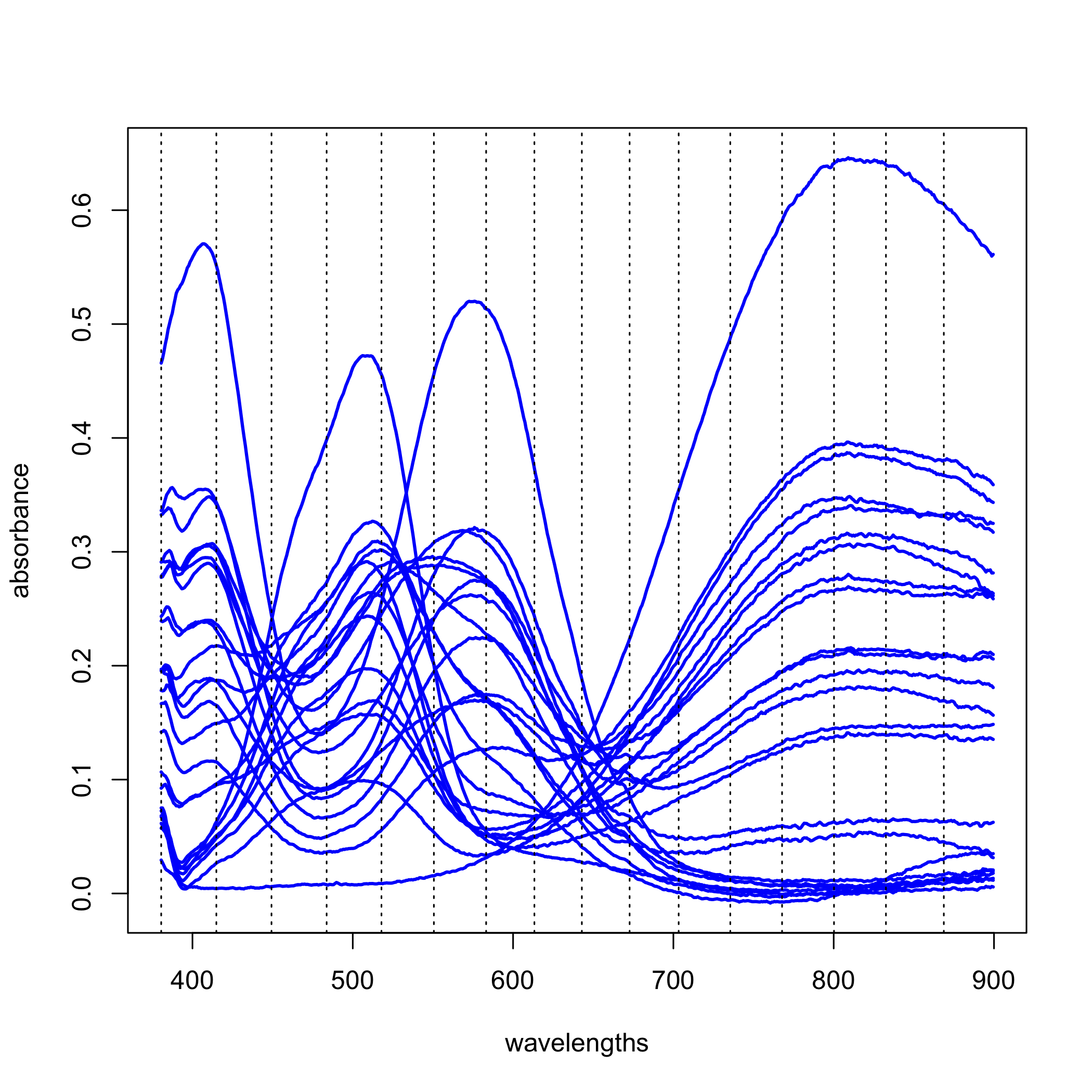
Cada componente principal representa una porción de las varianzas generales de los datos y cada componente principal sucesivo representa una proporción menor de la varianza general que el componente principal anterior. Aquellos componentes principales que dan cuenta de proporciones insignificantes de la varianza global presumiblemente representan ruido en los datos; los componentes principales restantes presumiblemente son determinados y suficientes para explicar los datos. La siguiente tabla proporciona un resumen de la proporción de la varianza general explicada por cada uno de los 16 componentes principales.

Cuadro\(\PageIndex{1}\): La proporción de varianza general explicada por los componentes principales para los datos de la figura\(\PageIndex{6}\).

	PC1	PC2	PC3	PC4	PC5	PC6	PC7	PC8
desviación estándar	3.3134	2.1901	0.42561	0.17585	0.09384	0.04607	0.04026	0.01253
proporción de varianza	0.6862	0.2998	0.01132	0.00193	0.00055	0.00013	0.00010	0.00001
proporción acumulativa	0.6862	0.9859	0.99725	0.99919	0.99974	0.99987	0.99997	0.99998
	PC9	PC10	PC11	PC12	PC13	PC14	PC15	PC16
desviación estándar	0.01049	0.009211	0.007084	0.004478	0.00416	0.003039	0.002377	0.001504
proporción de varianza	0.00001	0.000010	0.000000	0.000000	0.000000	0.000000	0.000000	0.000000
proporción acumulativa	0.99999	0.999990	1.000000	1.000000	1.000000	1.000000	1.000000	1.000000

El primer componente principal representa 68.62% de la varianza global y el segundo componente principal representa 29.98% de la varianza general. Colectivamente, estos dos componentes principales representan el 98.59% de la varianza general; sumar un tercer componente representa más del 99% de la varianza general. Claramente necesitamos considerar al menos dos componentes (tal vez tres) para explicar los datos en la Figura\(\PageIndex{1}\). Los 14 (o 13) componentes principales restantes simplemente dan cuenta del ruido en los datos originales. Esto nos deja con la siguiente ecuación relacionando los datos originales con las puntuaciones y cargas

\[ [D]_{24 \times 16} = [S]_{24 \times n} \times [L]_{n \times 16} \nonumber \]

donde\(n\) está el número de componentes necesarios para explicar los datos, en este caso dos o tres.

Para examinar más de cerca los componentes principales, trazamos las puntuaciones para PC1 contra las puntuaciones para PC2 para dar la gráfica de puntuaciones que se ve a continuación, que muestra las puntuaciones ocupando un espacio triangular.

Figura\(\PageIndex{7}\): Gráfica de puntuaciones para 24 muestras mostrando sus puntuaciones a lo largo del eje del primer componente principal y el eje del segundo componente principal.

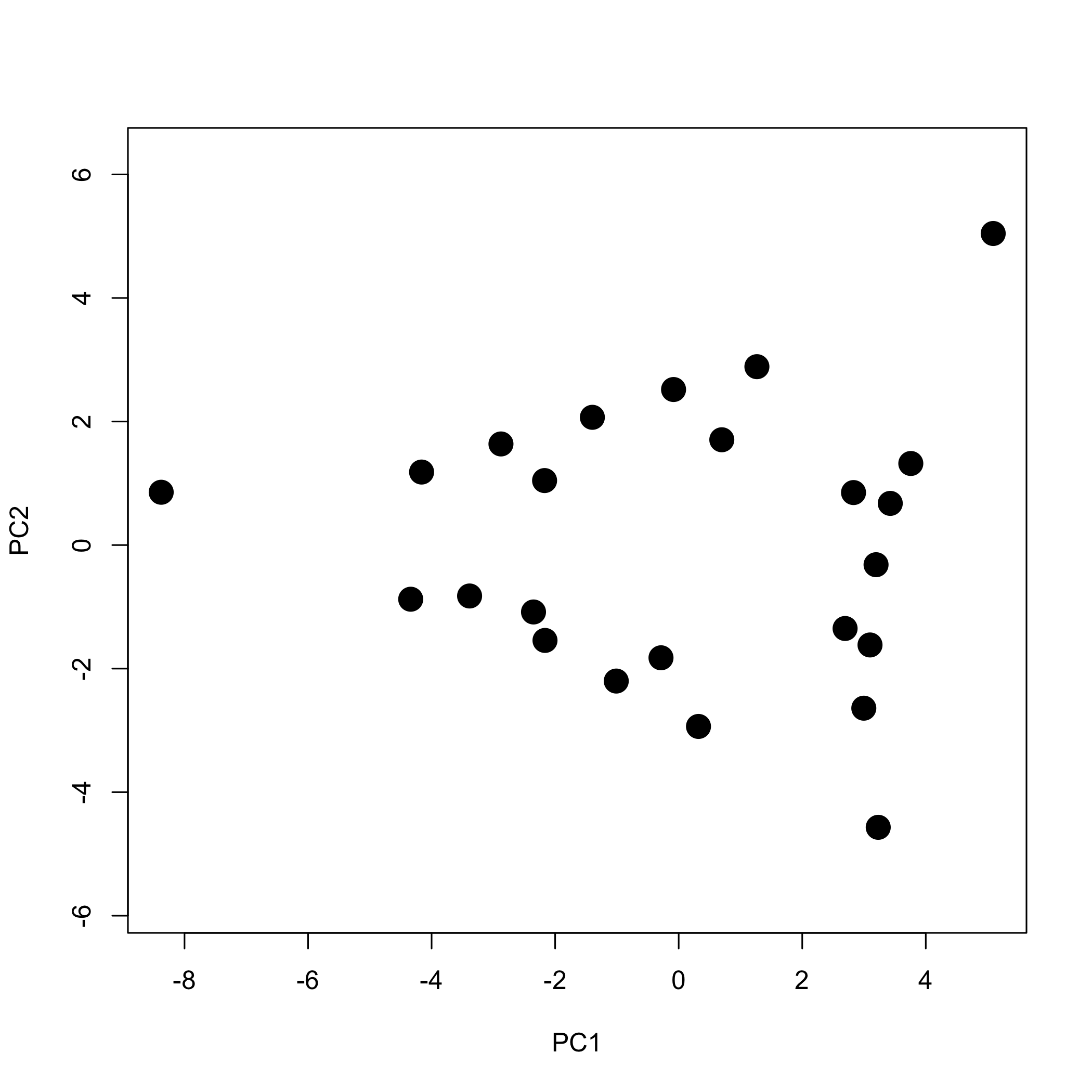
Debido a que nuestros datos son espectros visibles, es útil comparar la ecuación

\[ [D]_{24 \times 16} = [S]_{24 \times n} \times [L]_{n \times 16} \nonumber \]

a Beer's Law, que en forma de matriz es

\[ [A]_{24 \times 16} = [C]_{24 \times n} \times [\epsilon b]_{n \times 16} \nonumber \]

donde\([A]\) da los valores de absorbancia para las 24 muestras a 16 longitudes de onda,\([C]\) da las concentraciones de los dos o tres componentes que componen las muestras, y\([\epsilon b]\) da los productos de la absortividad molar y la longitud de trayectoria para cada uno de los dos o tres componentes en cada uno de los 16 longitudes de onda. La comparación de estas dos ecuaciones sugiere que las puntuaciones están relacionadas con las concentraciones de\(n\) los componentes y que las cargas están relacionadas con las absorbilidades molares de los\(n\) componentes. Además, podemos explicar el patrón de las puntuaciones en la Figura\(\PageIndex{7}\) si cada una de las 24 muestras consiste en un 1—3 analitos siendo los tres vértices muestras que contienen un solo componente cada uno, cayendo las muestras más o menos en una línea entre dos vértices siendo mezclas binarias de los tres analitos, y los puntos restantes son mezclas ternarias de los tres analitos.

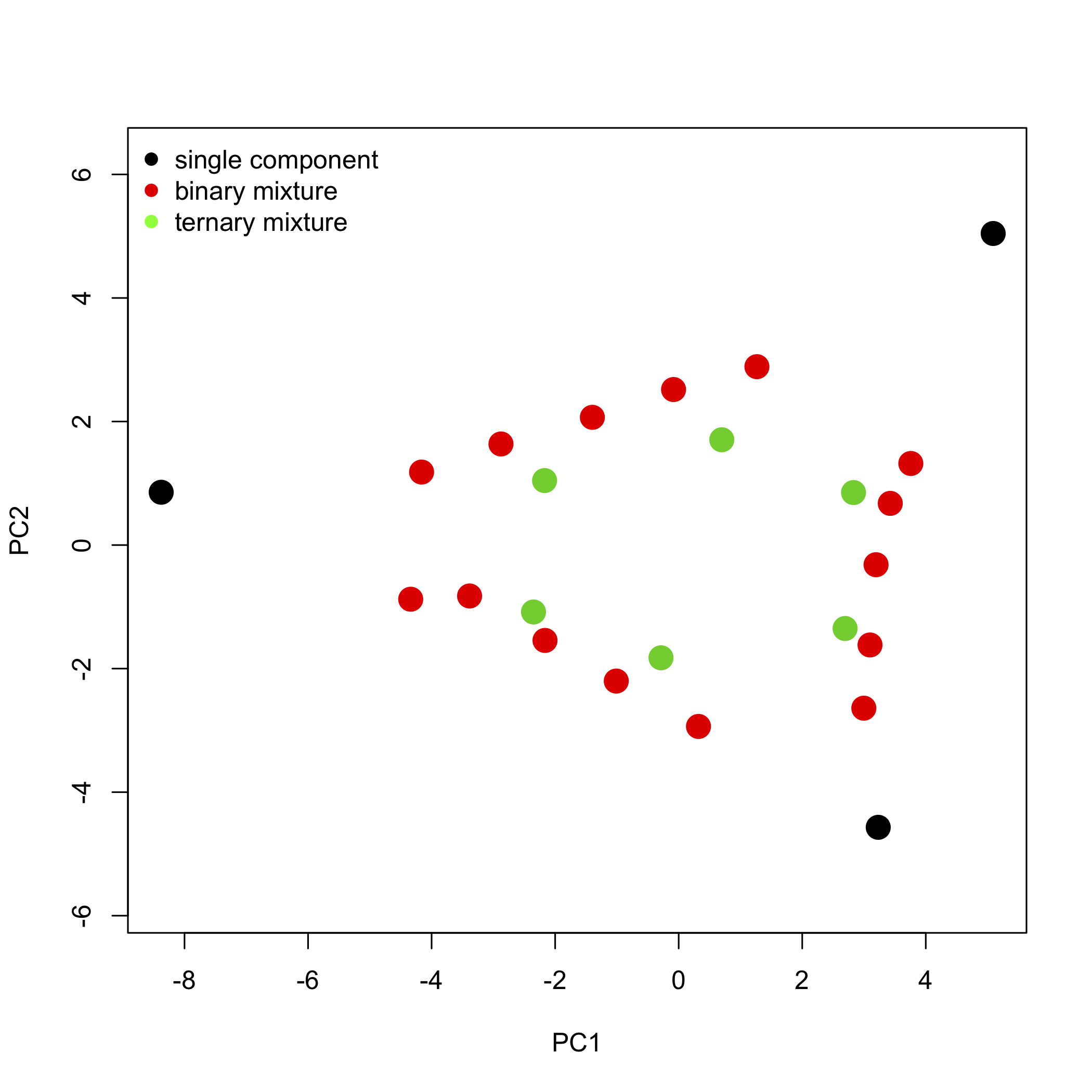
Figura\(\PageIndex{8}\): La gráfica de puntuaciones de la Figura codificada por\(\PageIndex{7}\) colores para mostrar muestras que contienen un componente, muestras que contienen dos componentes y muestras que contienen tres componentes. Tenga en cuenta que las mezclas binarias caen a lo largo de una línea (o arco suavemente curvo) que conecta dos muestras de un solo componente, y que las mezclas ternarias ocupan el espacio interior más interno definido por las muestras de un solo componente y mezclas binarias.

Nota

Si hay tres componentes en nuestras 24 muestras, ¿por qué dos componentes son suficientes para representar casi el 99% de la sobrevarianza? Supongamos que preparamos cada muestra usando una pipeta digital volumétrica para combinar partes alícuotas extraídas de soluciones de los componentes puros, diluyendo cada una a un volumen fijo en un matraz aforado de 10.00 mL. Por ejemplo, para hacer una mezcla ternaria podríamos pipetear en 5.00 mL de componente uno y 4.00 mL de componente dos. Si estamos diluyendo a un volumen final de 10 mL, entonces el volumen del tercer componente debe ser menor a 1.00 mL para permitir diluir a la marca. Debido a que el volumen del tercer componente está limitado por los volúmenes de los dos primeros componentes, dos componentes son suficientes para explicar la mayoría de los datos.

Las cargas, como se señaló anteriormente, están relacionadas con las absorbilidades molares de los componentes de nuestra muestra, proporcionando información sobre las longitudes de onda de la luz visible que son más absorbidas por cada muestra. Podemos sobreponer una gráfica de las cargas en nuestra gráfica de partituras (esto se llama biplot), como se muestra aquí.

Figura\(\PageIndex{9}\): Biplot que muestra las puntuaciones (puntos) y cargas (flechas) para nuestras 24 muestras y 16 longitudes de onda. La posición de las cargas con respecto a las puntuaciones proporciona información sobre la relación entre las dos. Por ejemplo, la carga para una longitud de onda de 703.3 nm se alinea casi perfectamente con las puntuaciones de la muestra 1, sugiriendo que esta longitud de onda es absorbida esencialmente por solo el componente único que compone esta muestra. La luz con una longitud de onda de 642.9 nm, sin embargo, tiene una carga que cae entre las puntuaciones para las muestras 1 y 2, lo que sugiere que es absorbida por el componente único que compone la muestra 1 y el componente único que compone la muestra 2.

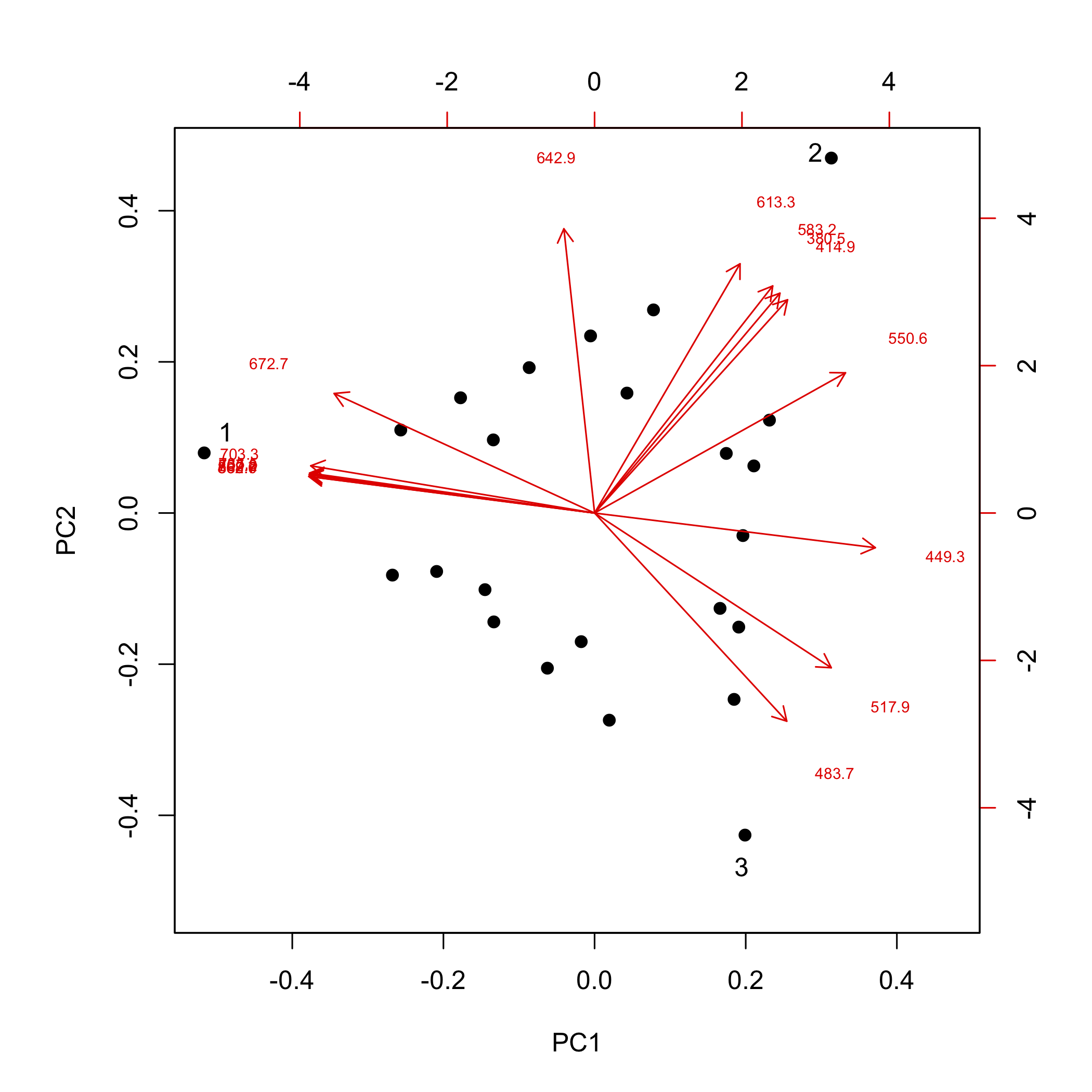
Cada flecha se identifica con una de nuestras 16 longitudes de onda y apunta hacia la combinación de PC1 y PC2 a la que está más fuertemente asociada. Por ejemplo, aunque difícil de leer aquí, todas las longitudes de onda de 672.7 nm a 868.7 nm (ver el subtítulo de Figura\(\PageIndex{6}\) para una lista completa de longitudes de onda) están fuertemente asociadas con el analito que compone la muestra de un solo componente identificada por el número uno, y las longitudes de onda de 380.5 nm, 414. 9 nm, 583.2 nm y 613.3 nm están fuertemente asociados con el analito que conforma la muestra de un solo componente identificada por el número dos.

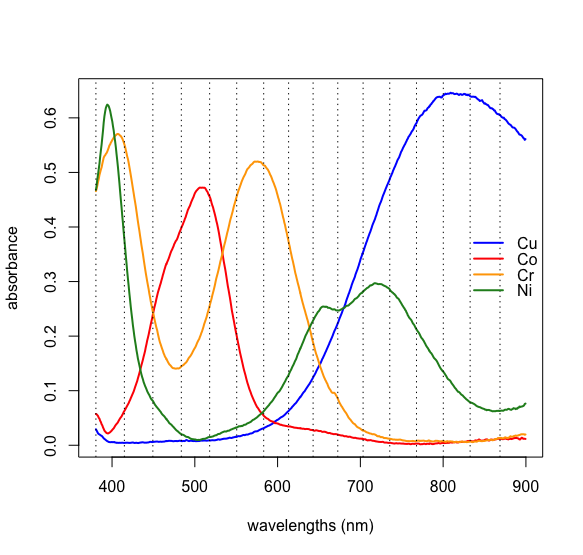
Si tenemos algún conocimiento sobre la posible fuente de los analitos, entonces podemos hacer coincidir las cargas experimentales con los analitos. Las muestras en la Figura\(\PageIndex{1}\) se realizaron utilizando soluciones de varios iones de metales de transición de primera fila. La figura\(\PageIndex{10}\) muestra los espectros visibles para cuatro iones metálicos de este tipo. Al comparar estos espectros con las cargas de la Figura se\(\PageIndex{9}\) muestra que el Cu ^{2 +} absorbe a las longitudes de onda más asociadas con la muestra 1, que Cr ^{3 +} absorbe a las longitudes de onda más asociadas con la muestra 2, y que el Co ^{2 +} absorbe a las longitudes de onda más asociadas con la muestra 3; el último de los iones metálicos, Ni ^{2 +}, no está presente en las muestras

Figura\(\PageIndex{10}\): Espectros visibles para los cuatro iones metálicos que podrían estar en las 24 muestras. De estos iones metálicos, Ni ^{2 +} (aq) no está presente en las muestras.