2.3: Fluido binario

Entropía de Mezcla

La termodinámica del proceso de mezcla es importante para los equilibrios de fases, hidrofobicidad, solubilidad y problemas de solvatación relacionados. El proceso de mezcla de dos sustancias puras\(A\) y\(B\) se muestra a continuación. Definimos la composición del sistema a través del número de\(A\) y\(B\) partículas:\(N_A\) y\(N_B\) y el número total de partículas\(N = N_A + N_B\), que también es igual al número de células. Comenzamos con dos recipientes de los fluidos puros homogéneos y los mezclamos, manteniendo constante el número total de celdas. En el caso de los fluidos puros antes de la mezcla, todas las celdas del recipiente se llenan inicialmente, por lo que solo hay un microestado accesible,\(\Omega_{\text{pure}} = 1\), y

\[S_{\text{pure}} = k_B \ln 1 = 0\nonumber\]

Cuando se mezclan los dos contenedores, el número de microestados posibles viene dado por la distribución binomial:\(\Omega_{\text{mix}} = N!/N_A! N_B!\).

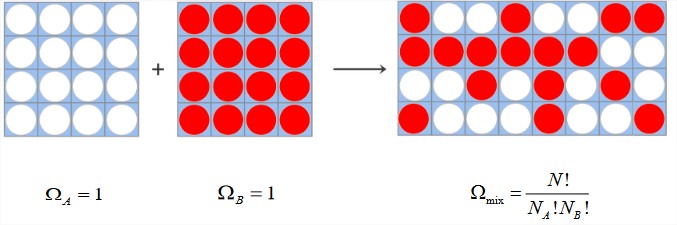
Si estas partículas no tienen interacciones, cada microestado es igualmente probable, y similar a la eq. (2.2.2) obtenemos la entropía de la mezcla como

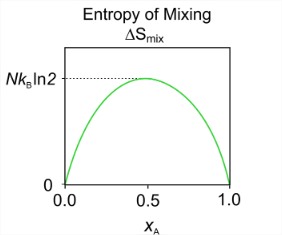
\[S_{\text{mix}}=-N k_{B}\left(x_{A} \ln x_{A}+x_{B} \ln x_{B}\right) \label{eq2.3.1}\]

Para la mezcla, definimos las fracciones molares para los dos componentes:\(x_A = N_A / N\) y\(x_B = N_B / N\). Como antes, desde\(x_A\) y\(x_B < 1\), la entropía para la mezcla siempre es positiva. Luego se calcula la entropía de mezcla a partir de\(\Delta S_{\text{mix}} = S_{\text{mix}} - (S_{\text{pure A}} + S_{\text{pure B}})\). Dado que la entropía de las sustancias puras en este modelo es cero,\(\Delta S_{\text{mix}} = S_{\text{mix}}\). Una gráfica de esta función en función de fracciones molares ilustra que tiene la mezcla de entropía máxima\(x_A = x_B = 0.5\).

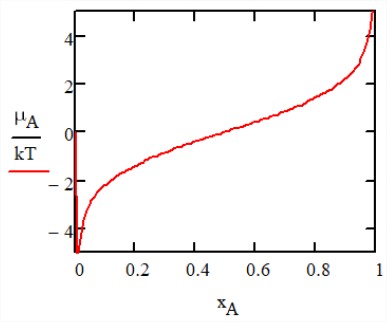
En ausencia de interacciones entre partículas, la energía libre de la mezcla es puramente entrópica con\(\Delta F_{\text{mix}} = -T \Delta S_{\text{mix}}\). El potencial químico de\(A\) las partículas\(\mu_A\) describe la energía libre necesaria para reemplazar una partícula\(B\) por una\(A\) partícula adicional, y se obtiene de

\[\begin{array} {l} {\mu_i = \left (\dfrac{\partial F}{\partial N_i} \right )_{T, V, \{N_{j \ne i}\}}} \\ {\mu_A = -k_B T (\ln x_A - \ln x_B) = -\mu B} \end{array} \nonumber\]

Esta curva ilustra el creciente desafío de encontrar espacio disponible a medida que aumenta la fracción de empaque.

Interacción intermolecular

Para observar los sistemas reales, ahora agregamos interacciones entre partículas asignando una energía de interacción\(\omega\) entre dos células que están en contacto. La energía de interacción puede ser positiva (desestabilizadora) o negativa (favorable).

Con la adición de interacciones intermoleculares, cada microestado tendrá una energía distinta, la función de partición canónica se puede obtener a partir de la eq. (2.1.1), y siguen otras propiedades termodinámicas.

En el caso de una mezcla, asignamos energías de interacción separadas para cada contiguo\(A-A\),\(B-B\), o\(A-B\) par en un microestado dado:\(\omega_{AA}, \omega_{BB}, \omega_{AB}\). ¿Cómo calculamos la energía de un microestado? m es el número total de contactos moleculares en el volumen, y estos pueden dividirse en\(A-A\),\(B-B\), o\(A-B\) contactos:

\[m = m_{AA} + m_{BB} + m_{AB} \nonumber\]

Si bien\(m\) es constante, los recuentos de contactos específicos\(m_{ij}\) varían según el microestado. Entonces la energía de la mezcla para el\(i^{th}\) microestado único se puede escribir como

\[E_{\text {mix}}=m_{A A} \omega_{A A}+m_{B B} \omega_{B B}+m_{A B} \omega_{A B} \label{eq2.3.2}\]

y la energía interna proviene de un promedio conjunto de esta cantidad. Un cálculo exacto de la energía interna de la función de partición requeriría una suma sobre todas las configuraciones posibles con sus números de contacto individuales. En cambio, podemos usar un enfoque más simple y aproximado que utiliza una estrategia que comienza expresando cada término en la eq. (\(\ref{eq2.3.2}\)) en términos de\(m_{AB}\). Sabemos:

\[\begin{array} {rcl} {m_{AA}} & = & {\text{(Total contacts for A) - (Contacts of A with B)}} \\ {} & = & {\dfrac{zN_A}{2} - \dfrac{m_{AB}}{2}} \end{array}\]

\[m_{B B}=\dfrac{z N_{B}}{2}-\dfrac{m_{A B}}{2}\]

Entonces tenemos

\[\begin{array} {rcl} {E_{\text{mix}}} & = & {\left (\dfrac{z\omega_{AA} N_A}{2} \right ) + \left (\dfrac{z\omega_{BB} N_B}{2} \right ) + m_{AB} \left (\omega_{AB} - \dfrac{\omega_{AA} + \omega_{BB}}{2} \right )} \\ {} & = & {U_{\text{pure A}} + U_{\text{pure B}} + m_{AB} \Delta \omega} \end{array} \label{eq2.3.5}\]

El último término en esta expresión es la mitad del cambio de energía de interacción para cambiar un\(A-A\) y un\(B-B\) contacto para formar dos\(A-B\) contactos:

\[\Delta \omega = \left (\omega_{A B} - \dfrac{\omega_{A A} + \omega_{B B}}{2} \right)\]

También reconocemos que los dos primeros términos son solo la energía de los dos líquidos puros antes de mezclarlos. Estos se calculan tomando el número de celdas en el líquido puro (\(N_i\)) multiplicado por el número de contactos por celda (\(z\)) y luego dividirlos por dos, para que no se cuenten dos veces los contactos.

\[U_{\text{pure, i}} = \dfrac{z \omega_{ii} N_{i}}{2}\]

Con estas expresiones, eq. (\(\ref{eq2.3.5}\)) se convierte

\[E_{\text{mix}} = U_{\text{pure A}} + U_{\text{pure B}} + m_{AB} \Delta \omega \nonumber\]

Esta ecuación describe la energía de un microestado en términos del número de\(A-B\) contactos presentes\(m_{AB}\).

En este punto, esto no es particularmente útil porque no es práctico enumerar todos los microestados posibles y sus correspondientes\(m_{AB}\). Para simplificar nuestro cálculo de\(U_{\text{mix}}\), hacemos una “aproximación media de campo”, que reemplaza\(m_{AB}\) con su promedio estadístico\(\langle m_{AB} \rangle\):

\[\begin{array} {rcl} {\langle m_{AB} \rangle} & = & {\text{(# of contact sites for A)} \times \text{(probability of contact site being B)}} \\ {} & = & {(N_A z) \left (\dfrac{N_B}{N}\right ) = zx_A x_B N} \end{array}\]

Entonces para la energía para el estado mixto\(U_{\text{mix}} = \langle E_{\text{mix}} \rangle\), obtenemos:

\[U_{\text{mix}} = U_{\text{pure A}} + U_{\text{pure B}} + x_A x_B Nk_B T \chi_{AB}\]

Aquí hemos introducido el parámetro de intercambio unitless,

\[\chi_{A B}=\dfrac{z}{k_{B} T} \left (\omega_{A B} - \dfrac{\omega_{A A}+\omega_{B B}}{2} \right ) = \dfrac{z \Delta \omega}{k_{B} T} \label{eq2.3.10}\]

que expresa\(\Delta \omega\) (el cambio de energía al conmutar un solo\(A\) y\(B\) del estado puro al otro líquido) en unidades de\(k_B T\). Dividir por\(z\) da la energía de interacción promedio por contacto.

\[\begin{array} {l} {\chi_{AB} > 0 \to \text{unfavorable A-B interaction}} \\ {\chi_{AB} < 0 \to \text{favorable A-B interaction}} \end{array} \nonumber\]

Ahora podemos determinar el cambio en la energía interna al mezclar:

\[\begin{array} {rcl} {\Delta U_{\text{mix}} } & = & {(U_{\text{mix}} - U_{\text{pure A}} - U_{\text{pure B}})} \\ {} & = & {x_A x_B N k_B T \chi_{AB}} \end{array} \label{eq2.3.11}\]

Nota en\(\Delta U_{mix}\) función de la composición tiene su valor mínimo para una mezcla con\(x_A = 0.5\), cuando\(\chi_{AB} < 0\).

Tenga en cuenta que en la aproximación del campo medio, la función de partición canónica es

\[Q = \dfrac{N!}{N_A! N_B!} q_A^{N_A} q_B^{N_B} \exp [-U_{\text{mix}}/k_B T]\nonumber\]

Mantuvimos aquí las funciones de partición molecular interna para completar, pero para las partículas simples en este modelo\(q_A = q_B = 1\).

Mezcla de Energía Libre ¹

Usando eqs. (\(\ref{eq2.3.1}\)) y (\(\ref{eq2.3.11}\)), ahora podemos obtener la energía libre de mezclar

\[\begin{array} {rcl} {\Delta F_{\text{mix}} } & = & {\Delta U_{\text{mix}} - T \Delta S_{\text{mix}} } \\ {} & = & {Nk_B T (x_A x_B \chi_{AB} + x_A \ln x_A + x_B \ln x_B)} \end{array}\nonumber\]

Esta función se representa a continuación como una función de la fracción molar para diferentes valores del parámetro de intercambio. Cuando no hay interacciones intermoleculares (\(\chi_{AB} = 0\)), la mezcla es espontánea para cualquier fracción molar y puramente entrópica. Cualquier\(A-B\) interacción fuertemente favorable (\(\chi_{AB} < 0\)) solo sirve para disminuir aún más la energía libre para todas las fracciones molares.

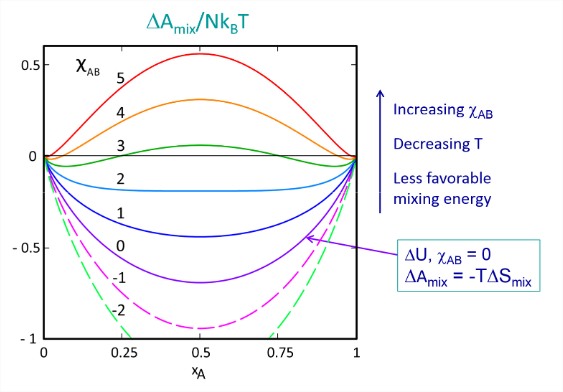
A medida que\(\chi_{AB}\) aumenta, vemos subir la energía libre para mezclar, con los mayores cambios para la mezcla 50/50. Para describir las consecuencias, veamos la curva para\(\chi_{AB} = 3\), para la cual ciertas composiciones son miscibles\((\Delta F_{\text{mix}} < 0)\) y otras inmiscibles\((\Delta F_{\text{mix}} > 0)\).

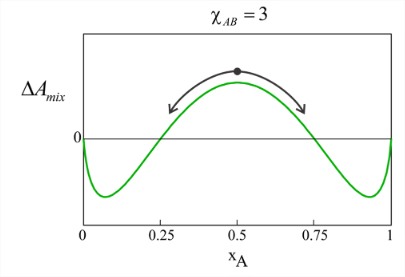
Considera qué pasaría si preparamos una mezcla 50/50 de esta solución. La energía libre de mezcla es positiva en la composición de equilibrio de la mezcla\(x_A= 0.5\) homogénea, lo que indica que los dos componentes son inmiscibles. Sin embargo, hay otras composiciones de mezcla que sí tienen una energía libre negativa de mezcla. Bajo estas condiciones la solución puede separarse en dos fases de tal manera que\((\Delta F_{\text{mix}}\) se minimiza. Esto ocurre en fracciones molares de\(x_A\) = 0.07 & 0.93, lo que nos muestra que una fase se caracterizará por\(x_A \gg x_B\) y la otra con\(x_A \ll x_B\). Si preparamos una mezcla desigual con positivo\((\Delta A_{\text{mix}}\), por ejemplo\(x_A = 0.3\), el sistema seguirá separándose de forma espontánea aunque la conservación de masa dictará que la masa total de la fracción con\(x_A = 0.07\) será mayor que la masa de la fracción en\(x_A = 0.93\). A\(\chi_{AB}\) medida que aumenta más allá de 3, la fracción molar del componente menor disminuye como se esperaba para el efecto hidrófobo. Considera si\(A\) = agua y\(B\) = petróleo. \(\omega_{BB}\)y\(\omega_{AB}\) son pequeños y negativos,\(\omega_{AA}\) es grande y negativo, y\(\chi_{AB} \gg 1\).

Comportamiento Crítico

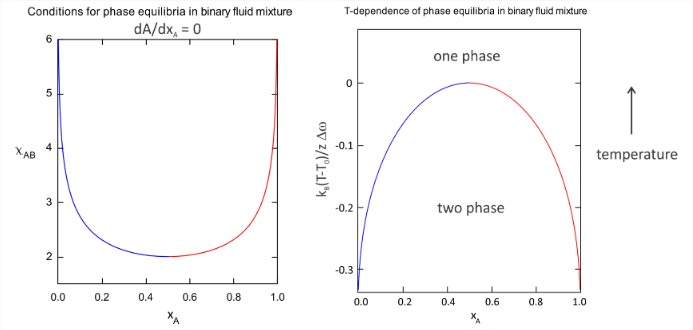
Tenga en cuenta que las mezclas 50/50 con\(2 < \chi_{AB} < 2.8\) tienen una energía libre negativa de mezcla para crear una sola fase homogénea, sin embargo, el sistema aún puede reducir la energía libre aún más por separación de fases. Como se ve en la figura,\(\chi_{AB} = 2\) marca un cruce de mezclas de una fase a mezclas de dos fases, que es la firma de un punto crítico. Podemos encontrar las condiciones para los equilibrios de fase mediante la localización de los mínimos de energía libre en función de\(\chi_{AB}\), lo que conduce a los diagramas de fase en función de\(\chi_{AB}\) y\(T\) por debajo. La temperatura crítica para el cruce del comportamiento de una a dos fases es\(T_0\), y\(\Delta \omega\) es el cambio diferencial promedio en la energía de interacción definido en eq. (\(\ref{eq2.3.10}\)).

Lecturas

1. K. Dill y S. Bromberg, Impulsores Moleculares: Termodinámica Estadística en Biología, Química, Física y Nanociencia. (Taylor & Francis Group, Nueva York, 2010).
2. W. W. Graessley, Líquidos poliméricos y redes: estructura y propiedades. (Garland Science, Nueva York, 2004), Cap. 3.

_____________________________________

1. J. H. Hildebrand y R. L. Scott, Regular Solutions. (Prentice-Hall, Englewood Cliffs, N.J., 1962).