6.1: Electrostática

Propiedades Eléctricas del Agua y Soluciones Acuosas

Queremos entender las propiedades energéticas y eléctricas y el transporte de iones y moléculas cargadas en el agua. Se trata de fuerzas fuertes. Considere un ejemplo de\(\ce{NaCl}\) disociación en energía de disociación en fase gaseosa\(\Delta H_{\text{ionization}} \approx 270\ kJ/mol\):

\ [K_ {\ texto {ionización}} (\ texto {gas}) =\ dfrac {\ izquierda [\ mathrm {Na} ^ {+}\ derecha]\ izquierda [\ mathrm {Cl} ^ {-}\ derecha]} {[\ mathrm {NaCl}]}\ aprox 10^ {-89}
\ nonumber\]

En solución, este proceso [\(\ce{NaCl} (aq) \to \text{Na}^+ (aq) + \text{Cl}^- (aq)\)] ocurre espontáneamente; el producto de solubilidad para\(\ce{NaCl}\) es\(K_{\text{sp}} = [\text{Na}^+ (aq)][\text{Cl}^- (aq)] / [\ce{NaCl} (aq)] = 37\). Del mismo modo, las moléculas de agua son átomos de hidrógeno y oxígeno unidos covalentemente, pero sabemos que las fuerzas internas en el agua pueden autoionizar una molécula de agua:

\[K_{\text {ionization }}(\text { gas })=\left[\mathrm{H}^{+}\right]\left[\mathrm{OH}^{-}\right] \approx 10^{-75} \text { and } K_{W}\left(\mathrm{H}_{2} \mathrm{O}\right) = \left[\mathrm{H}^{+}\right] \left [\mathrm{OH}^{-} \right]=10^{-14} \nonumber\]

Estas tremendas diferencias se originan en las enormes fuerzas electrostáticas colectivas que están presentes en el agua. “Solvación polar” se refiere a la manera en que los dipolos de agua estabilizan las cargas.

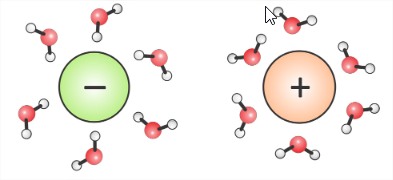
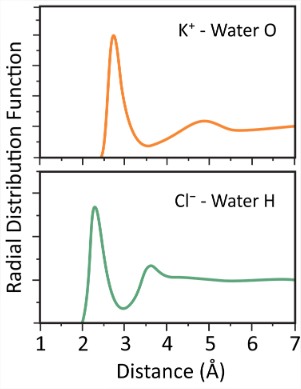
Estos dipolos son simplificaciones de los reordenamientos de la estructura del agua para acomodar y disminuir la energía del ion. Es importante recordar que el agua es un medio polarizable en el que los enlaces de hidrógeno modifican drásticamente las propiedades electrostáticas.

Electrostática

Revisemos una serie de resultados de la electrostática clásica. Las interacciones entre objetos cargados pueden formularse usando la fuerza, el campo eléctrico o el potencial electrostático. El potencial es nuestra consideración principal cuando se discuten las energías libres en la termodinámica y la hamiltoniana en la mecánica estadística. Describiremos estos, consideremos la interacción entre dos iones\(A\) y\(B\), separados por una distancia\(r_{AB}\), con cargas\(q_A\) y\(q_B\).

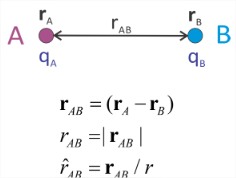
Fuerza y Trabajo

La Ley de Coulomb da la fuerza que\(B\) ejerce sobre\(A\).

\[\boldsymbol{f}_{A B}=-\dfrac{1}{4 \pi \varepsilon} \dfrac{q_{A} q_{B}}{r_{A B}^{2}} \hat{r}_{A B}\nonumber\]

\(\hat{r}_{AB}\)es un vector unitario que apunta desde\(\mathbf{r}_B\) a\(\mathbf{r}_A\). Una identidad útil para recordar para los cálculos es

\[\dfrac{e^{2}}{4 \pi \varepsilon_{0}}=230 p N /n m^{2}\nonumber\]

Para fines termodinámicos es útil calcular el trabajo reversible para un proceso. El trabajo eléctrico proviene del movimiento de cargas contra una fuerza

\[d w=-\boldsymbol{f} \cdot d \mathbf{r} \nonumber\]

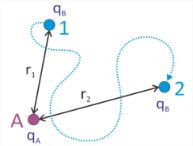
Siempre y cuando q y ε sean independientes de r, y el proceso sea reversible, entonces el trabajo solo depende de r, y es independiente del camino. Para mover la partícula B del punto 1 en una separación r ₀ al punto 2 en una separación r requiere el siguiente trabajo\ [
w_ {1\ rightarrow 2} =\ frac {1} {4\ pi\ varepsilon} q_ {A} q_ {B}\ left (\ frac {1} {r_ {2}} -\ frac {1} {r_ {1}\ derecha)
\]

y si la ruta vuelve a la posición inicial,\(w_{rev} = 0\).

Campo, E

El campo eléctrico es una cantidad vectorial que describe la acción de las cargas en un punto en el espacio. El campo de la partícula cargada\(B\) en el punto\(A\) es

\[\mathbf{E}_{A B}\left(\mathbf{r}_{A}\right)=-\dfrac{1}{4 \pi \varepsilon} \frac{q_{B}}{r_{A B}^{2}} \hat{r}_{A B} \nonumber\]

\(\mathbf{E}_{AB}\)está relacionado con la fuerza que\(B\) ejerce la partícula sobre una partícula de prueba cargada\(A\) con carga\(q_A\) a través de

\[\mathbf{f}_{A} = q_{A} \mathbf{E}_{A B}\left(\mathbf{r}_{A}\right)\nonumber\]

Si bien la fuerza en el punto a depende del signo y la magnitud de la carga de prueba, el campo no. Más generalmente, el campo ejercido por múltiples partículas cargadas en el punto\(\mathbf{r}_A\) es la suma vectorial del campo a partir de múltiples cargas (\(i\)):

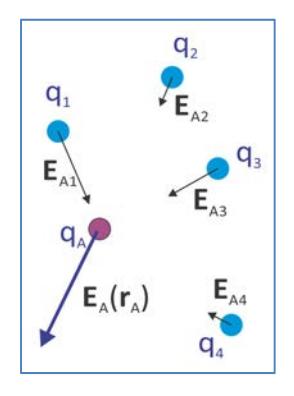
\[\mathbf{E}\left(\mathbf{r}_{A}\right)=\sum_{i} \mathbf{E}_{A i}\left(\mathbf{r}_{A}\right)=-\dfrac{1}{4 \pi \varepsilon} \sum_{i} \dfrac{q_{i}}{r_{A i}^{2}} \hat{r}_{A i}\nonumber\]

donde\(r_{Ai} = \left |\mathbf{r}_A - \mathbf{r}_i \right|\) y el vector de unidad\(\hat{A}_{Ai} = (\mathbf{r}_A - \mathbf{r}_i)/r_{Ai}\). Alternativamente, para una densidad de carga continua\(\rho_q (\mathbf{r})\),

\[\mathbf{E}\left(\mathbf{r}_{A}\right)=-\dfrac{1}{4 \pi \varepsilon} \int \rho_{q}(\mathbf{r}) \dfrac{\left(\mathbf{r}_{A}-\mathbf{r}\right)}{\left|\mathbf{r}_{A}-\mathbf{r}\right|^{3}} d \mathbf{r}\nonumber\]

donde la integral está sobre un volumen.

Potencial electrostático,\(\Phi\)

Para termodinámica y mecánica estadística, deseamos expresar interacciones eléctricas en términos de energía o potencial electrostático. Mientras que la fuerza y el campo son cantidades vectoriales, el potencial electrostático\(\Phi\) es una cantidad escalar que está relacionada con el campo eléctrico a través de

\[\mathbf{E}=-\bar{\nabla} \Phi \nonumber\]

Cuenta con unidades de energía por unidad de carga. El potencial electrostático en el punto\(\mathbf{r}_A\), que resulta de una carga puntual en\(\mathbf{r}_B\), es

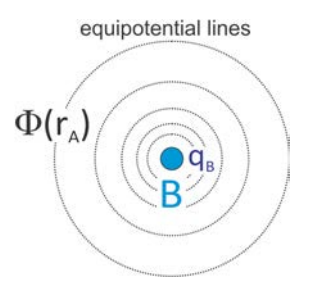
\[\Phi \left(r_{A}\right)=\dfrac{1}{4 \pi \varepsilon} \dfrac{q_{B}}{r_{A B}}\]

El potencial eléctrico es aditivo en la contribución de múltiples cargas:

\ [
\ Phi\ izquierda (r_ {A}\ derecha) =\ dfrac {1} {4\ pi\ varepsilon}\ suma_ {i}\ dfrac {q_ {i}} {r_ {A i}}\ quad\ text {o}\ quad\ phi\ izquierda (r_ {A}\ derecha) =\ dfrac {1} {4\ pi varepsilon}\ int\ dfrac {\ rho_ {q} (\ mathbf {r})} {\ izquierda|\ mathbf {r} _ {A} -\ mathbf {r}\ derecha|} d\ mathbf {r}
\ nonumber\]

La energía electrostática de una partícula\(A\) como resultado del potencial debido a la partícula\(B\) es

\ [
U_ {A B}\ izquierda (r_ {A}\ derecha) =q_ {A}\ Phi\ izquierda (r_ {A}\ derecha) =\ dfrac {1} {4\ pi\ varepsilon}\ dfrac {q_ {A} q_ {B}} {r_ {A}} {r_ {A}}\ nonumber
\]

Tenga en cuenta que\(U_{A B}=q_{A} \Phi\left(r_{A}\right)=q_{B} \Phi\left(r_{B}\right)=\tfrac{1}{2}\left(q_{A} \Phi\left(r_{A}\right)+q_{B} \Phi\left(r_{B}\right)\right)\), así podemos generalizar esto para calcular la energía potencial almacenada en una colección de múltiples cargas como

\ [
\ begin {alineado}
U &=\ dfrac {1} {2}\ sum_ {i} q_ {i}\ Phi\ izquierda (r_ {A i}\ derecha)\\
&=\ frac {1} {2}\ int\ Phi_ {A}\ izquierda (\ mathbf {r} _ _ {A}\ derecha)\ rho_ {q}\ izquierda (\ mathbf {r} _ {A}\ derecha)\ rho_ {q}\ izquierda (\ mathbf {r} _ {A} {r} _ _ {A}\ derecha) d\ mathbf {r} _ _ {A}
\ final {alineado}\ nonumber
\]