6.8: Distribuciones de iones cerca de una esfera cargada
- Page ID
- 69714
Distribuciones de iones cerca de una esfera cargada 1
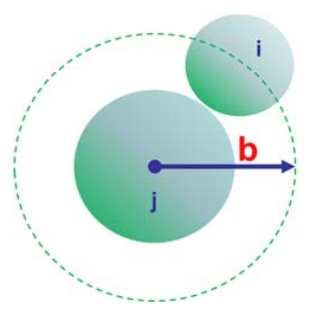
Ahora veamos cómo se distribuirán los iones alrededor de una esfera cargada. Esta esfera podría ser una proteína u otro ion. Asumimos una distribución de carga esféricamente simétrica sobre los iones, y una distribución de Boltzmann para la distribución de carga para los iones (\(i\)) alrededor de la esfera (\(j\)) de la forma
\[\rho (r) = \sum_i ez_i C_{0, i} e^{-z_i e \Phi_j (r) /k_B T}\]
\(\Phi_j (r)\)es el potencial electrostático en el radio\(r\) que resulta de una carga puntual\(z_j e\) en el centro de la esfera. Adicionalmente, asumimos que la esfera es una pared dura, y definimos un radio de acercamiento más cercano por iones en solución,\(b\). El PBE se convierte en
\[\dfrac{1}{r^2} \dfrac{d}{dr} \left (r^2 \dfrac{d\Phi}{dr} \right ) = \dfrac{1}{\varepsilon} \sum_i ez_i C_{0, i} e^{-z_i e \Phi_j (r) /k_B T} \nonumber\]
Para simplificar esto, nuevamente aplicamos la aproximación Debie-Hückel\((ze\Phi \ll k_B T)\), expandimos el exponencial en eq., bajamos el término principal debido a la condición de neutralidad de carga, y obtenemos
\[\rho (r) = -\sum_i C_{0, i} z_i^2 e^2 \Phi_j (r)/k_B T \label{eq6.8.2}\]
Entonces el PBE linealizado está en la aproximación Debie-Hückel es
\[\dfrac{1}{r^2} \dfrac{d}{dr} \left (r^2 \dfrac{d\Phi}{dr} \right ) = \kappa^2 \Phi \label{eq6.8.3}\]
Como antes:\(\kappa^2 = \lambda_D^{-2} = 2e^2 I/\varepsilon k_B T\). Soluciones a eq. (\(\ref{eq6.8.3}\)) tomará la forma:
\[\Phi = A_1 \dfrac{e^{-\kappa r}}{r} + A_2 \dfrac{e^{\kappa r}}{r} \label{eq6.8.4}\]
Para resolver este uso condiciones de contorno:
- \(A_2 = 0\), ya que\(\Phi \to 0\) en\(r = \infty\).
- El campo en la superficie de una esfera con carga\(z_j e\) y radio\(b\) se determina a partir de
\[4\pi b^2 E(b) = \dfrac{z_j e}{\varepsilon} \label{eq6.8.5}\]
Ahora, usando
\[E(b) = -\dfrac{d\Phi}{dr}|_{r = b} \label{eq6.8.6}\]
Sustituir eq. (\(\ref{eq6.8.4}\)) en RHS y eq. (\(\ref{eq6.8.5}\)) en LHS de eq. (\(\ref{eq6.8.6}\)). Resolver para\(A_1\).
\[A_1 = \dfrac{z_j e e^{\kappa b}}{4\pi \varepsilon (1 + \kappa b)}\nonumber\]
Entonces, el potencial electrostático para\(r \ge b\) es
\[\Phi (r) = \underbrace{\dfrac{z_j e}{4\pi \varepsilon_0 r}}_{\text{vacuum}} \dfrac{e^{-\kappa (r - b)}}{\varepsilon_r (1 + \kappa b)} \label{eq6.8.7}\]
El ajuste nos\(r = b\) da el potencial superficial de la esfera:
\[\Phi (b) = \dfrac{z_j e}{4\pi \varepsilon b (1 + \kappa b)}\nonumber\]
Anote el factor exponencial en eq. (\(\ref{eq6.8.7}\)) dice que\(\Phi\) cae más rápido que\(r^{-1}\) como resultado del tamizaje. Ahora sustituya la eq. (\(\ref{eq6.8.7}\)) en eq. (\(\ref{eq6.8.2}\)) obtenemos la densidad de probabilidad de carga
\[\rho (r) = \dfrac{-\kappa^2 z_j e}{4\pi r} \dfrac{e^{-\kappa (r - b)}}{1 + \kappa b}\]
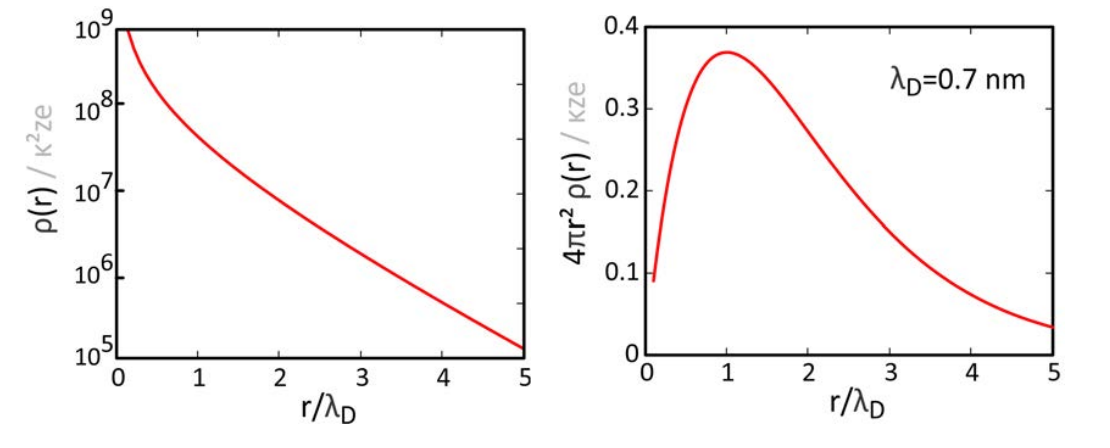
Vemos que la densidad de carga sobre los iones cae como\(e^{-\kappa (r - b)}/r\), una función de rápida descomposición que enfatiza la fuerte tendencia de los iones a atraer o repeler a corto alcance. Sin embargo, la densidad de carga entre\(r\) y\(r + dr\) es\(4\pi r^2 \rho (r)\) y por lo tanto crece linealmente con r antes de decaer exponencialmente:\(r e^{-\kappa (r - b)}\). Se grafica esta función para ilustrar el grosor de la “nube iónica” alrededor de la esfera, que tiene su punto máximo\(r = \lambda_D\). Adicionalmente, tenga en cuenta, que la distribución de carga alrededor de ese ion es igual y opuesta a la carga de la esfera "\(j\)”.
\[\int_b^{\infty} \rho (r) 4 \pi r^2 dr = -z_j e\nonumber\]
También es posible calcular las funciones de distribución radial para iones en el límite de Debye-Hückel. 2 La función de distribución de pares radiales para iones de tipo\(i\) y\(j\)\(g_{ij} (r)\),, está relacionada con el potencial de fuerza media\(W_{ij}\) como
\[g_{ij} (r) = \exp [-W_{ij} (r) / k_B T]\]
Si sólo se consideran los efectos electrostáticos, podemos aproximarnos\(W_{ij}\) como la energía de interacción\(U_{ij} (r) = z_i e\Phi_j (r)\). Usando el resultado Debye—Hückel, eq. (\(\ref{eq6.8.7}\)),
\[U_{ij} (r) = \dfrac{z_i z_j e^2}{4\pi \varepsilon (1 + \kappa b)} \dfrac{e^{-\kappa (r - b)}}{r} \nonumber\]
Veamos la forma de\(g(r)\) para dos iones de carga individual con\(\lambda_D = 0.7\ nm\),\(\epsilon = 80\), y\(T = 300\ K\). La longitud de Bjerrum se calcula como\(\ell_B = e^2/4\pi \epsilon k_B T = 0.7\ nm\). Dado que el Debye—Hückel se mantiene\(ze\Phi \ll k_B T\), podemos expandir lo exponencial en eq. como
\[g_{ij} (r) = 1 - \chi_{ij} + \dfrac{1}{2} \chi_{ij}^2 + \cdots \nonumber\]
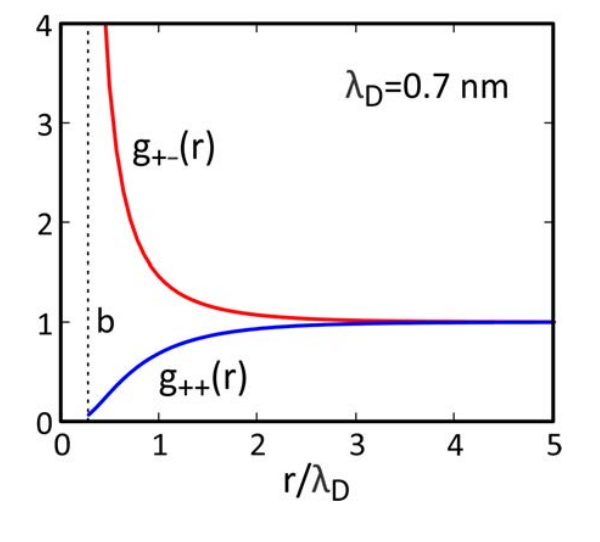
donde definimos\(\chi_{ij} = U_{ij} (r) /k_B T = \ell_B e^{-\kappa (r - b)} r^{-1} (1 + \kappa b)^{-1}\). La función de distribución radial resultante para co- y contraiones calculados para se\(b = 0.15\ nm\) muestran a continuación.
Lecturas
- M. Daune, Biofísica Molecular: Estructuras en Movimiento. (Oxford University Press, Nueva York, 1999), Cap. 16, 18.
- D. A. McQuarrie, Mecánica Estadística. (Harper & Row, Nueva York, 1976), Cap. 15.
______________________________
- Ver M. Daune, Biofísica Molecular: Estructuras en Movimiento. (Oxford University Press, Nueva York, 1999), Ch. 16.; D. A. McQuarrie, Mecánica estadística. (Harper & Row, Nueva York, 1976), Ch. 15.; Y. Marcus, Radios iónicos en soluciones acuosas, Chem. Rev. 88 (8), 1475-1498 (1988).
- Véase D. A. McQuarrie, Mecánica Estadística. (Harper & Row, Nueva York, 1976), Cap. 15.

