6.7: Distribuciones de iones cerca de una interfaz cargada

Aproximación Debie-Hückel

Describir iones cerca de un plano cargado negativamente es una manera de describir la capa difusa de cationes que se forma cerca de la interfaz de carga negativa en bicapas lipídicas. El enfoque más simple es usar la ecuación de Debie-Hückel (PBE linealizado) en una dimensión. \(x\)es la distancia del plano cargado infinito con una densidad de carga superficial de\(\sigma = q/a\).

\[\dfrac{\partial^2 \Phi (x)}{\partial x^2} = \dfrac{1}{\lambda_D^2} \Phi (x)\nonumber\]

Generalmente, la solución es

\[\Phi (x) = a_1 e^{-x/\lambda_D} + a_2 e^{x/\lambda_D} \label{eq6.7.1}\]

Aplicar condiciones de contorno:

1. \(\lim_{x \to \infty} \Phi (x) = 0\)\(\therefore a_2 = 0\)
2. El campo eléctrico para superficie con densidad de carga σ (del teorema de Gauss)

\[E = - \dfrac{\partial \Phi}{\partial x} |_{\text{surface}} = \dfrac{\sigma}{\varepsilon} \label{eq6.7.2}\]

Diferenciar eq. (\(\ref{eq6.7.1}\)) y comparar con la eq. (\(\ref{eq6.7.2}\)):

\[a_1 = \dfrac{\sigma \lambda_D}{\varepsilon} \nonumber\]

El potencial electrostático decae exponencialmente lejos de la superficie hacia cero.

\[\Phi (x) = \dfrac{\sigma \lambda_D}{\varepsilon} e^{-x/\lambda_D} \nonumber\]

Nominalmente, el prefactor sería el “potencial superficial” en\(x = 0\), pero la aproximación de Debye lo subestimaría significativamente, como veremos más adelante. Sustituir\(\Phi\) en la ecuación de Poisson da

\[\rho (x) = \dfrac{-\sigma}{\lambda_D} e^{-x/\lambda_D} \label{eq6.7.3}\]

La densidad de distribución de iones en solución decae exponencialmente con la distancia. Esta descripción es válida para potenciales débiles, o\(x > \lambda_D\). El potencial y la densidad de carga son proporcionales como\(\Phi (x) = -\lambda_D^2 \rho (x)/\varepsilon \); ambos decaen exponencialmente en la escala de la longitud de Debye a largo alcance.

Nota:

Mayor concentración de iones\(\to\) menor\(\lambda_D \to\) Doble capa menos difusa.

Mayor temperatura\(\to\) más grande\(\lambda_D \to\) Doble capa más difusa.

Tenga en cuenta también que la carga superficial se equilibra por la distribución de iones en solución:

\[\sigma = -\int_0^{\infty} \rho (x) dx\]

que puedes confirmar sustituyendo la eq. (\(\ref{eq6.7.3}\)).

Gouy-Chapman Modelo ¹

Para describir adecuadamente el comportamiento iónico para distancias más cortas (\(x < \lambda_D\)), no es necesario hacer la aproximación de potencial débil y puede retener la forma no lineal de la ecuación de Poisson—Boltzmann:

\[\begin{array} {rcl} {\dfrac{\partial^2 \Phi (x)}{\partial x^2}} & = & {\dfrac{2zeC_0}{\varepsilon} \text{sinh} \left (\dfrac{ze \Phi (x)}{kT} \right )} \\ {E} & = & {-\dfrac{\partial \Phi}{\partial x}|_{\text{surf}} = \dfrac{4\pi \ell_B \sigma k_B T}{e^2}} \end{array} \nonumber\]

De hecho, esta forma sí tiene una solución analítica. Es útil definir un potencial electrostático reducido adimensional, expresado en unidades eléctricas térmicas:

\[\underline{\Phi} = \dfrac{e}{k_B T} \Phi \nonumber\]

y una distancia reducida que se escala por la longitud de Debye

\[\underline{x} = x/\lambda_D \nonumber \]

Luego, el PBE para un electrolito 1:1 toma una forma simple

\[\nabla^2 \underline{\Phi} (x) = \text{sinh} \underline{\Phi} (x)\nonumber\]

con la solución:

\[\underline{\Phi} (\underline{x}) = 2 \ln \left (\dfrac{1 + ge^{-\underline{x}}}{1 - ge^{-\underline{x}}} \right )\nonumber\]

Aquí\(g\) hay una constante, que podemos relacionar con el potencial superficial, poniéndola\(x\) a cero.

\[\exp (-\underline{\Phi} (0)/2) = \dfrac{1 - g}{1 + g} = -\text{tanh} (\ln (g) /2)\nonumber\]

\(\underline{\Phi} (0)\)es el potencial superficial escalado. Usando la densidad de carga superficial\(\sigma\) podemos encontrar:

\[g = - \dfrac{x_0}{\lambda_D} + \sqrt{1 + \left (\dfrac{x_0}{\lambda_D} \right )^2} \text{ with } x_0 = \dfrac{e}{2\pi \ell_B \sigma} \nonumber\]

Entonces puedes obtener la distribución de iones a partir de la ecuación de Poisson:\(\rho (x) = \varepsilon \nabla^2 \Phi (x)\).

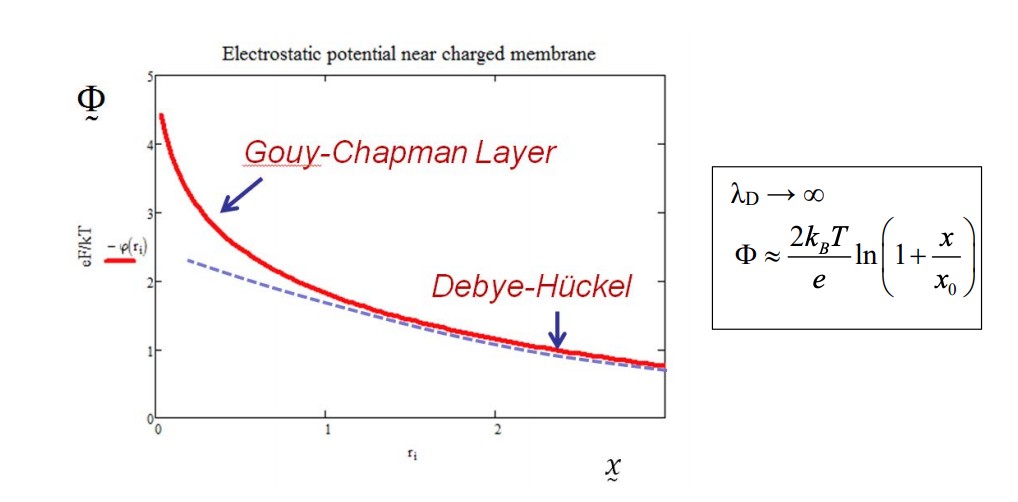
La capa Gouy-Chapman, es decir\(x < \lambda_D\), tiene interacciones iónicas lo suficientemente fuertes como para que vea una mejora sobre Debye—Hückel.

Capa de popa

En proximidad inmediata a una superficie fuertemente cargada, se puede formar una capa de contactos directos de contraiones en la superficie: la capa Stern. La capa de popa gobierna el plano de deslizamiento para la difusión de partículas cargadas. El potencial zeta\(\zeta\) es la diferencia de energía potencial entre la capa Stern y la región electroneutral de la muestra, y gobierna la movilidad electroforética de las partículas. Se calcula a partir del trabajo requerido para llevar una carga desde\(x = \infty\) la superficie de la capa Stern.

_______________________________

1. H. H. Girault, Electroquímica Analítica y Física. (CRC Press, Nueva York, 2004).; M. B. Jackson, Biofísica Molecular y Celular. (Cambridge University Press, Cambridge, 2006), cap. 11.; M. Daune, Molecular Biophysics: Structures in Motion. (Oxford University Press, Nueva York, 1999), Ch. 18.; S. McLaughlin, Las propiedades electrostáticas de las membranas, Anni. Rev. Biofías. Biofías. Chem. 18, 113-136 (1989).