7.1: Modelos de Segmento

Modelos de Segmento ¹

• \((n + 1)\)cuentas enlazan por\(n\) segmentos o enlaces de longitud\(\ell\).
• Cada cuenta tiene una posición\(\vec{r_i}\).
• A cada enlace se le asigna un vector,\(\vec{\ell_i} = \vec{r_i} - \vec{r_{i - 1}}\).
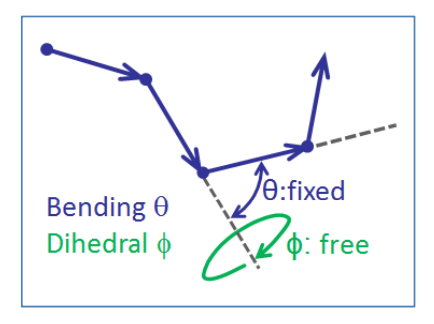
• El ángulo de flexión entre segmentos adyacentes\(i\) y\((i + 1)\) es\(\theta_i\):\(\cos \theta = \vec{\ell_i} \cdot \vec{\ell_{i - 1}}\)
• Para cada ángulo de flexión hay un ángulo diedro asociado\(\phi_i\) definido como la rotación del segmento\((i+1)\) fuera del plano definido por segmentos\(i\) y\((i - 1)\).
• Hay ángulos\(n - 1\) separados de flexión y diedro.

Variables estadísticas para macromoléculas

Distancia de extremo a extremo

La longitud del contorno es la longitud completa del polímero a lo largo del contorno de la cadena:

\[L_C = n \ell\nonumber\]

Cada cadena tiene la misma longitud de contorno, pero dimensiones variables en el espacio que resultan de la flexibilidad conformacional. La variable estructural primaria para medir esta variación conformacional es el vector de extremo a extremo entre la primera y la última perla\(\vec{R} = \vec{r_n} - \vec{r_0}\), o equivalentemente

\[\vec{R} = \sum_{i = 1}^{n} \vec{\ell_i}\nonumber\]

Estadísticamente, las dimensiones de un polímero se pueden caracterizar por las estadísticas de la distancia de extremo a extremo. Considere su valor cuadrático medio:

\[\langle \vec{R}^2 \rangle = \langle \vec{R} \cdot \vec{R} \rangle = \left \langle \left (\sum_{i = 1}^{n} \vec{\ell_i} \right ) \cdot \left (\sum_{j= 1}^{n} \vec{\ell_j} \right ) \right \rangle\]

Después de expandir estas sumas, podemos recolectar dos conjuntos de términos: (1) los autotérminos con\(i = j\) y (2) las correlaciones de interconexión\((i \ne j)\):

\[\begin{array} {rcl} {\langle \vec{R}^2 \rangle } & = & {n \ell^2 + \sum_{j \ne i} \langle \vec{\ell_i} \cdot \vec{\ell_j} \rangle} \\ {} & = & {n \ell^2 + \ell^2 \sum_{j \ne i} \langle \cos \theta_{ij} \rangle} \end{array} \label{eq7.1.1}\]

Aquí\(\theta_{ij}\) está el ángulo entre segmentos\(i\) y\(j\). Este segundo término describe cualquier posible preferencia conformacional entre segmentos a lo largo de la cadena. Llamaremos al factor\(\langle \cos \theta_{ij} \rangle\) la función de correlación de orientación del segmento, que también está escrita

\[\begin{array} {rcl} {g(k)} & = & {\langle \cos \theta_k \rangle} \\ {\theta_k} & = & {\vec{\ell_i} \cdot \vec{\ell_{i + k}} \ \ \ \ \ \ \ \ k = |j - i|} \end{array}\]

Aquí\(k\) se refiere a la separación entre dos segmentos. Esta función de correlación puede variar en valor de 1 a -1, donde +1 representa una cadena altamente alineada o extendida y los valores negativos serían muy condensados o compactos. No\((g = 0)\) se esperan correlaciones entre bandas para la colocación de segmentos por una caminata aleatoria.

La correlación interbond se puede insertar en modelos de segmentos, tanto a través de reglas ad hoc, como aplicando una función de energía que restringe las interacciones entre segmentos. Por ejemplo, la función de energía torsional a continuación,\(U_{\text{conf}}\), se usaría para ponderar la probabilidad de que los segmentos adyacentes adopten un ángulo de torsión particular. Una función general de energía torsional\(U_{\text{conf}} (\Theta)\) involucra todos los ángulos\(2(n-1)\) posibles\(\Theta = \{\theta_1, \phi_1, \theta_2, \phi_2, ... \theta_{n-1}, \phi_{n-1} \}\), la densidad de probabilidad conjunta para adoptar una conformación particular es

\[P(\Theta) = \dfrac{e^{-U_{\text{conf}} (\Theta)/k_B T}}{\int d \Theta e^{-U_{\text{conf}} (\Theta)/k_B T}} \nonumber\]

La integral sobre\(\Theta\) refleja\(2(n - 1)\) integrales sobre coordenadas polares para todos los segmentos adyacentes,

\[\int d \Theta = \int_{0}^{\pi} \int_{0}^{2\pi} \sin \theta_1 d \theta_1 d \phi_1 \cdots \int_{0}^{\pi} \int_{0}^{2\pi} \sin \theta_{n - 1} d \theta_{n - 1} d \phi_{n - 1} \nonumber\]

Entonces la función de correlación de alineación es

\[\langle \vec{\ell_i} \cdot \vec{\ell_j} \rangle = \ell^2 \int d \Theta \cos \theta_{ij} P (\Theta) \nonumber\]

Esta no es una forma práctica, por lo que haremos suposiciones simplificadoras sobre la forma de esta distribución de probabilidad. Por ejemplo, si alguna configuración de segmentos depende solo de sus vecinos más cercanos entonces\(P(\Theta) = P(\theta, \phi)^{(n - 1)}\).

Longitud de persistencia

Para cualquier polímero, la alineación de cualquier par de vectores en la cadena se vuelve no correlacionada a lo largo de una secuencia de segmentos lo suficientemente larga. Para cuantificar esta distancia definimos una “longitud de persistencia”\(\ell_p\).

\[\ell_p = \langle \hat{\ell_i} \cdot \sum_{j = 1}^{n} \vec{\ell_j} \rangle \ \ \ \ \hat{\ell_i} = \dfrac{\vec{\ell_i}}{|\ell |} \nonumber\]

Esta es la distancia característica a lo largo de la cadena para el decaimiento para la función de correlación orientacional entre vectores de enlace,

\[g(k) = \ell ^2 \langle \cos^k \theta \rangle \nonumber\]

¿Cómo se comportará esto? Si consideras eso\(|\cos \theta | < 1\), entonces\(\langle \cos^k \theta \rangle \) caerá con el aumento\(k\), acercándose a cero como\(k \to \infty\). Esa es la memoria de la alineación entre dos vectores de enlace cae con su separación, donde está la escala de distancia para la pérdida de correlación\(\ell_p\). Por lo tanto, esperamos una forma monótonamente en descomposición para esta función:

\[g(k) = \ell^2 e^{-k \ell / \ell_p} \label{eq7.1.3}\]

Para los modelos continuos de varilla delgada del polímero, esta expresión se escribe en términos de la distancia del contorno\(s\), el desplazamiento a lo largo del contorno de la cadena (es decir,\(s = \ell k\)),

\[g(s) = \ell^2 e^{- |s|/\ell_p} \nonumber\]

¿Cómo nos relacionamos\(\theta\) y\(\ell_p\)? ² Escribir\(\langle \cos^k \theta \rangle \approx \exp (k \ln [\langle \cos \theta \rangle ])\) y equiparar esto con la eq. (\(\ref{eq7.1.3}\)) indica que

\[\ell_p = -\ell \ln \langle \cos \theta \rangle \nonumber\]

Para cadenas rígidas, podemos aproximarnos\(\ln (x) \approx (1 - x)\), entonces

\[\ell_p \approx \dfrac{\ell }{1 - \langle \cos \theta \rangle} \nonumber\]

Radio de giro

El radio de giro es otra variable estructural importante que está estrechamente relacionada con los observables experimentales. Aquí las dimensiones del polímero se expresan como extensión relativa al centro de masa para la cadena.

Esto resulta útil para polímeros ramificados y heteropolímeros (como proteínas). Denotando la posición y masa de la\(i^{\text{th}}\) perla como\(\vec{r_i}\) y\(m_i\), definimos el centro de masa para el polímero como una posición media ponderada en masa de las perlas en el espacio:

\[\vec{R_0} = \dfrac{\sum_{i = 0}^{n} m_i \vec{r_i}}{\sum_{i = 0}^{n} m_i} \nonumber\]

El índice de suma que comienza en 0 pretende reflejar la suma sobre\(n+1\) cuentas. El denominador de esta expresión es la masa total del polímero\(M = \sum_{i = 0}^{n} m_i\). Si todas las cuentas tienen la misma masa, entonces\(m_i/M = 1/(n + 1)\) y\(R_0\) es la media geométrica de sus posiciones.

\[\vec{R_0} = \dfrac{1}{n + 1} \sum_{i = 0}^{n} \vec{r_i}\nonumber\]

El radio de giro\(R_G\) para una configuración del polímero describe la distribución ponderada en masa de las perlas\(R_0\), y se define a través de

\[\langle R_G^2 \rangle = \dfrac{1}{n + 1} \sum_{i = 0}^n \langle \vec{S_i^2} \rangle \nonumber\]

donde\(\vec{S_i}\) es el radio de giro, es decir, la distancia radial del\(i^{\text{th}}\) cordón desde el centro de masa

\[\begin{array} {rcl} {\vec{S}_i^2 = \dfrac{m_i }{M} (\vec{r_i} - \vec{R}_0)^2} & \ & {\text{(mass-weighted)}} \\ {\vec{S}_i^2 = \dfrac{1}{n + 1} (\vec{r_i} - \vec{R}_0)^2} & \ & {\text{(equal mass beads)}} \end{array}\nonumber\]

Adicionalmente, podemos mostrar que el radio cuadrático medio de giro está relacionado con la separación promedio de todas las perlas de la cadena.

\[\langle R_G^2 \rangle = \dfrac{1}{(n + 1)^2} \sum_{i = 0}^n \sum_{j = 0}^n \langle (\vec{r_i} - \vec{r_j})^2 \rangle \nonumber\]

Cadena libremente articulada

La cadena libremente articulada describe una macromolécula como un esqueleto para el cual todos son posibles\(\theta\) y\(\phi\) son igualmente probables, y no hay correlaciones entre segmentos. Se le conoce como una “cadena ideal” porque no hay interacciones entre perlas o volumen excluido, y la configuración de la cadena principal del polímero sigue una caminata aleatoria. Si colocamos la primera cuenta en\(r = 0\), nos encontramos con eso\(\langle R \rangle = 0\), como se esperaba para una caminata aleatoria, y eq. (\(\ref{eq7.1.1}\)) reduce a

\[\langle R^2 \rangle = n \ell^2 \nonumber\]

\[\text{ or } R_{rms} = \langle R^2 \rangle^{1/2} = \sqrt{n} \ell \nonumber\]

Aunque la distancia promedio de extremo a extremo puede ser cero, la varianza en la distribución de extremo a extremo es

\[\sigma_r = \sqrt{\langle R^2 \rangle - \langle R \rangle^2} = \sqrt{n} \ell \nonumber\]

El radio de giro para una cadena ideal es:

\[R_G = \sqrt{\dfrac{\langle R^2 \rangle }{6}} = \sqrt{\dfrac{n \ell^2}{6}}\nonumber\]

Bobina Aleatoria Gaussiana

La cadena articulada libremente también se conoce como bobina aleatoria gaussiana, ya que las estadísticas de su configuración están completamente descritas por\(\langle R \rangle\) y\(\langle R^2 \rangle\), los dos primeros momentos de una distribución de probabilidad gaussiana de extremo a extremo\(P(R)\). La densidad de probabilidad de extremo a extremo en una dimensión se puede obtener a partir de una caminata aleatoria con pasos de\(n\) igual tamaño de longitud\(\ell\) en una dimensión, donde los pasos hacia adelante y hacia atrás son igualmente probables. Si el primer cordón en el que se fijó\(x_0 = 0\), entonces el último cordón se coloca por el último paso en la posición\(x\). En el límite continuo:

\[P(x, n) = \sqrt{\dfrac{1}{2\pi n \ell^2}} e^{-x^2/2n \ell^2}\label{eq7.1.4} \]

\(P(x, n) dx\)es la probabilidad de encontrar el extremo de la cadena con\(n\) cuentas a una distancia entre\(x\) y\(x+dx\) desde su primera perla. Tenga en cuenta que esto equipara la distancia rms de extremo a extremo con la desviación estándar para esta distribución:\(\langle R^2 \rangle = \sigma^2 = n \ell^2\).

Generalizar la eq. (\(\ref{eq7.1.4}\)) a una cadena tridimensional, reconocemos que la propagación en el\(x, y\), y\(z\) dimensiones es igualmente probable, por lo que la densidad de probabilidad 3D se puede obtener a partir de un producto de densidades de probabilidad 1D\(P(r) = P(x) P(y) P(z)\). Adicionalmente, debemos considerar la restricción de que la distribución de las distancias de extremo a extremo es igual en cada dimensión:

\[\langle \vec{R}^2 \rangle = \sigma_x^2 + \sigma_y^2 + \sigma_z^2 = n \ell^2 \nonumber\]

y desde entonces\(\sigma_x^2 = \sigma_y^2 = \sigma_z^2\),

\[\langle \vec{R}^2 \rangle = 3 \sigma_x^2 = n \ell^2 \nonumber\]

Por lo tanto,

\[\begin{array} {rcl} {P(r, n)} & = & {\sqrt{1}{2\pi \sigma_x^2} e^{-x^2/2 \sigma_x^2} \sqrt{1}{2\pi \sigma_y^2} e^{-x^2/2 \sigma_y^2} \sqrt{1}{2\pi \sigma_z^2} e^{-x^2/2 \sigma_z^2} } \\ {} & = & {\left (\dfrac{3}{2\pi \sigma^2} \right )^{3/2} e^{-3r^2/2\sigma^2}} \end{array} \nonumber\]

Para simplificar, definimos un parámetro de escalado con dimensiones de longitud inversa

\[\beta = \sqrt{\dfrac{3}{2n \ell^2}} = \sqrt{\dfrac{3}{2}} \langle R^2 \rangle^{-1/2} \nonumber\]

Entonces, la densidad de probabilidad en coordenadas cartesianas,

\[P(x, y, z, n) = \dfrac{\beta^3}{\pi^{3/2}} e^{-\beta^2 r^2} \ \ \ \text{ where } r^2 = x^2 + y^2 + z^2 \nonumber\]

Tenga en cuenta que las unidades de\(P(x, y, z, n)\) son volumen o concentración inversas. La probabilidad de encontrar el final de una cadena de\(n\) cuentas en una caja de volumen dx dy dz en la posición\(x, y, z\) es\(P(x, y, z, n)\ dx\ dy\ dz\). Esta función ilustra que la distancia de extremo a extremo más probable para un polímero de caminata aleatoria está en el origen. Por otro lado, también podemos expresar esto como una densidad de probabilidad radial que da la probabilidad de encontrar el final de una cadena en un radio entre\(r\) y\(r+dr\) desde el origen. Dado que el volumen de una concha esférica crece en proporción a su superficie:

\[P(r, n) dr = 4 \pi r^2 P(x, y, z, n) dr\nonumber\]

\[P(r, n) = 4\pi r^2 \left (\dfrac{3}{2\pi n \ell^2} \right )^{3/2} \exp \left [-\dfrac{3}{2} \dfrac{r^2}{n \ell^2} \right ]\]

Las unidades de\(P(r, n)\) son longitud inversa. Para la cadena articulada libremente, vemos que\(\beta^{-1} = \sqrt{2\langle R^2 \rangle /3}\) es la distancia de extremo a extremo más probable.

Cadena Giratoria Libreamente

Una extensión a la cadena de unión libre que agrega una única restricción configuracional que se asemeja mejor a la unión real en polímeros es la cadena que gira libremente. En este caso, el ángulo de la columna vertebral\(\theta\) tiene un valor fijo, y el ángulo diedro\(\phi\) puede girar libremente.

Para describir las dimensiones de la cadena, necesitamos evaluar las correlaciones de unión angular entre segmentos. Centrándonos primero en los segmentos adyacentes, sabemos que después de promediar sobre todo\(\phi\), lo fijo lo\(\theta\) asegura\(\langle \vec{\ell_i} \cdot \vec{\ell_{i+1}} \rangle = \ell^2 \cos \theta\). Para el siguiente segmento de la serie, solo el componente paralelo a\(\vec{\ell_{j + 1}}\) contribuirá a las correlaciones de enlace secuenciales a medida que promediamos sobre\(\phi_{i + 2}\):

\[\begin{array} {rcl} {\langle \vec{\ell_i} \cdot \vec{\ell_{i + 2}} \rangle} & = & {\langle \cos (\theta_i) \cos (\theta_{i + 1}) - \sin (\theta_i) \sin (\theta_{i + 1}) \cos (\phi_{i + 1}) \rangle} \\ {} & = & {\ell^2 \cos^2 \theta} \end{array}\nonumber\]

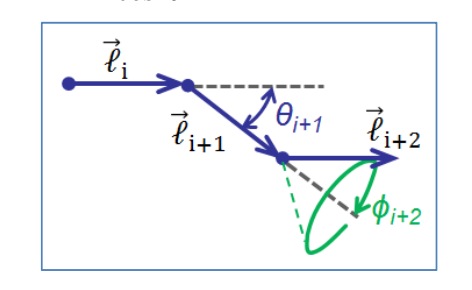
Ampliar este razonamiento lleva a la observación

\[\langle \vec{\ell_i} \cdot \vec{\ell_j} \rangle = \ell^2 (\cos \theta)^{j - i} \nonumber\]

Para evaluar las correlaciones de enlace en esta expresión, es útil definir un índice para la separación entre dos vectores de enlace:

\[k = j - i\nonumber\]

y

\[\alpha = \cos \theta \nonumber\]

Entonces la función de correlación de orientación del segmento es

\[g(k) = \langle \vec{\ell_i} \cdot \vec{\ell_j} \rangle = \ell^2 \alpha^k \nonumber\]

Para una separación\(k\) en una cadena de longitud\(n\), hay\(n-k\) posibles combinaciones de ángulos de unión,

\[\sum_{j \ne i} \langle (\cos \theta)^{j - i} \rangle = \sum_{k = 1}^{n - 1} (n - k) \alpha^k \nonumber\]

\[\therefore \ \ \ \ \ \langle R^2 \rangle = n \ell^2 + \ell^2 \sum_{k = 1}^{n - 1} (n - k) \alpha^k \nonumber\]

De esto se puede obtener

\[\langle R^2 \rangle = n \ell^2 \left (\dfrac{1 + \alpha}{1 - \alpha} - \dfrac{2\alpha (1 - \alpha^n)}{n (1 - \alpha)^2} \right ) \nonumber\]

En el límite de las cadenas largas (\(n \to \infty\)), encontramos

\[\langle R^2 \rangle \to n \ell^2 \left ( \dfrac{1 + \alpha}{1 - \alpha} \right )\nonumber\]

y

\[R_G = \sqrt{\dfrac{n \ell^2}{6} \left ( \dfrac{1 + \alpha}{1 - \alpha} \right )}\nonumber\]

Diedros restringidos

Cuando también se modifica la cadena que gira libremente para restringir el ángulo diedro\(\phi\), podemos resolver la distancia cuadrática media de extremo a extremo en el límite\(n \to \infty\). Dado un ángulo diedro promedio,

\[\beta = \langle \cos \phi \rangle \nonumber\]

\[\langle R^2 \rangle = n \ell^2 \left (\dfrac{1 + \alpha}{1 - \alpha} \right ) \left (\dfrac{1 + \beta}{1 - \beta} \right ) \nonumber\]

Comportamiento no ideal

Relación característica de Flory

Los polímeros reales son rígidos y han excluido el volumen, pero el comportamiento de\(R \sim \sqrt{n}\) incrustación generalmente se mantiene en general\(n (R \gg \ell_p)\). Para caracterizar la no idealidad, utilizamos la relación característica de Flory:

\[C_n = \dfrac{\langle R^2 \rangle}{n \ell^2} \nonumber\]

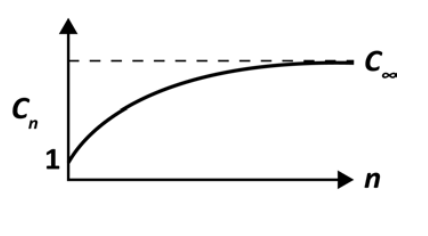
Para cadenas articuladas libremente\(C_n = 1\). Para cadenas no ideales con correlaciones angulares,\(C_n > 1\). Cn depende de la longitud de la cadena\(n\), pero debe tener un valor asintótico para grandes\(n\):\(C_{\infty}\). Por ejemplo, si examinamos cadenas largas que giran libremente

\[C_{\infty} = \lim_{n \to \infty} \dfrac{\langle R^2 \rangle}{n \ell^2} = \dfrac{1 + \alpha}{1 - \alpha} \ \ \ \ \ \alpha = \cos \theta \nonumber\]

(En la práctica, este límite suele ser para\(n > 30\)). Considere un polímero unido tetraédricamente con ángulo completo\(109^{\circ}\) (\(\theta = 54^{\circ}\)). entonces\(\cos \theta = 1/3\), y\(C_n = 2\). En la práctica, alcanzamos el límite de cadena larga\(C_{\infty}\) en\(n \approx 10\). Esta relación funciona bien para poliglicina y polietilenglicol (PEG).

Segmento estadístico o longitud de Kuhn

Qué tan rígido o flexible es un polímero depende de la escala de longitud de observación. Lo que es rígido en una escala es flexible para otra. Para un polímero infinitamente largo, siempre se puede encontrar una escala de longitud para la cual sus estadísticas son las de una bobina aleatoria gaussiana. Como resultado para un polímero de segmento, se puede imaginar reescalar segmentos continuos en un “segmento efectivo” más largo que puede no representar dimensiones atómicas, sino que se define para corresponder a un polímero de caminata aleatoria, con\(C_n = 1\). Entonces, la longitud efectiva del segmento es\(\ell_e\) (también conocida como la longitud de Kuhn) y el número de segmentos efectivos es\(n_e\). Luego se aplican las ecuaciones de cadena articuladas libremente:

\[\begin{array} {c} {L_C = n_e \ell_e} \\ {\langle R^2 \rangle = n_e \ell_e^2} \end{array} \nonumber\]

A partir de estas ecuaciones,\(\ell_e = \langle R^2 \rangle /L_C\). Vemos que\(\ell_e \gg \ell\) se aplica a las cadenas rígidas, mientras que\(\ell_e \approx \ell\) son flexibles.

También podemos escribir la longitud del contorno como\(L_C = \gamma n \ell\), donde\(\gamma\) es un factor geométrico < 1 que describe la restricción en los ángulos de unión. Para una cadena que gira libremente:\(\gamma = \cos (\theta /2)\). Usando las expresiones de cadena larga\((n \to \infty)\):\(\langle R^2 \rangle = C_{\infty} n \ell^2\), encontramos

\[\begin{array} {c} {\ell_e = \left (\dfrac{C_{\infty}}{\gamma } \right ) \ell} \\ {n _{\ell} = \left (\dfrac{\gamma^2}{C_{\infty}} \right ) n} \\ {\ell_p = \left (\dfrac{C_{\infty} + 1}{2} \right ) \ell } \end{array} \nonumber\]

Valores representativos para modelos de segmento de polímero

	\(C_{\infty}\)	\((n_e/n)\)	\(\ell\)(nm)	\(\ell_e\)(nm)	\(\gamma\)	\(\ell_p\)(nm)
Polietileno	\ (C_ {\ infty}\) ">6.7	\ ((n_e/n)\) "> (n > 10)	\ (\ ell\) (nm) ">0.154	\ (\ ell_e\) (nm) ">1.24	\ (\ gamma\) ">0.83	\ (\ ell_p\) (nm) ">
CLAVIJA	\ (C_ {\ infty}\) ">3.8	\ ((n_e/n)\) ">	\ (\ ell\) (nm) ">	\ (\ ell_e\) (nm) ">0.34	\ (\ gamma\) ">	\ (\ ell_p\) (nm) ">
Polialanina	\ (C_ {\ infty}\) ">9	\ ((n_e/n)\) "> (n > 70)	\ (\ ell\) (nm) ">0.38	\ (\ ell_e\) (nm) ">3.6	\ (\ gamma\) ">0.95	\ (\ ell_p\) (nm) ">0.5
Poliprolina	\ (C_ {\ infty}\) ">90	\ ((n_e/n)\) "> (n > 700)	\ (\ ell\) (nm) ">	\ (\ ell_e\) (nm) ">	\ (\ gamma\) ">	\ (\ ell_p\) (nm) ">5-10
dsDNA	\ (C_ {\ infty}\) ">86	\ ((n_e/n)\) ">	\ (\ ell\) (nm) ">0.35	\ (\ ell_e\) (nm) ">30-100	\ (\ gamma\) ">1	\ (\ ell_p\) (nm) ">50
ssDNA	\ (C_ {\ infty}\) ">	\ ((n_e/n)\) ">	\ (\ ell\) (nm) ">	\ (\ ell_e\) (nm) ">	\ (\ gamma\) ">	\ (\ ell_p\) (nm) ">1.5
Celulosa	\ (C_ {\ infty}\) ">	\ ((n_e/n)\) ">	\ (\ ell\) (nm) ">	\ (\ ell_e\) (nm) ">	\ (\ gamma\) ">	\ (\ ell_p\) (nm) ">6.2
Actin	\ (C_ {\ infty}\) ">	\ ((n_e/n)\) ">	\ (\ ell\) (nm) ">	\ (\ ell_e\) (nm) ">16700	\ (\ gamma\) ">	\ (\ ell_p\) (nm) ">10000-20000

____________________________________________

1. C. R. Cantor y P. R. Schimmel, Química Biofísica Parte III: El Comportamiento de las Macromoléculas Biológicas. (W. H. Freeman, San Francisco, 1980), Ch. 18.; K. Dill y S. Bromberg, Fuerzas impulsoras moleculares: termodinámica estadística en biología, química, física y nanociencia. (Taylor & Francis Group, Nueva York, 2010); P. J. Flory, Principles of Polymer Chemistry. (Prensa de la Universidad de Cornell, Ítaca, 1953).
2. C. R. Cantor y P. R. Schimmel, Química Biofísica Parte III: El Comportamiento de las Macromoléculas Biológicas. (W. H. Freeman, San Francisco, 1980), Ch. 19 p. 1033.