22.2: Dinámica informática

Existen varias formas de modelar computacionalmente procesos dependientes del tiempo en biofísica molecular. Estos métodos integran ecuaciones de movimiento para los grados moleculares de libertad que evolucionan bajo un potencial clásico de interacción fuerza-campo, un hamiltoniano mecánico cuántico o un paisaje energético que podría ser fenomenológico o atomisticamente detallado. Los ejemplos incluyen el uso de campos de fuerza clásicos para propagar la ecuación de movimiento de Newton, integrar la ecuación de Schrödinger o integrar la ecuación de Langevin en un potencial de fuerza media. Dado que nuestro interés está más en la descripción de datos computacionales o experimentales, esto solo será una breve descripción.

Dinámica clásica desde un potencial (campo de fuerza)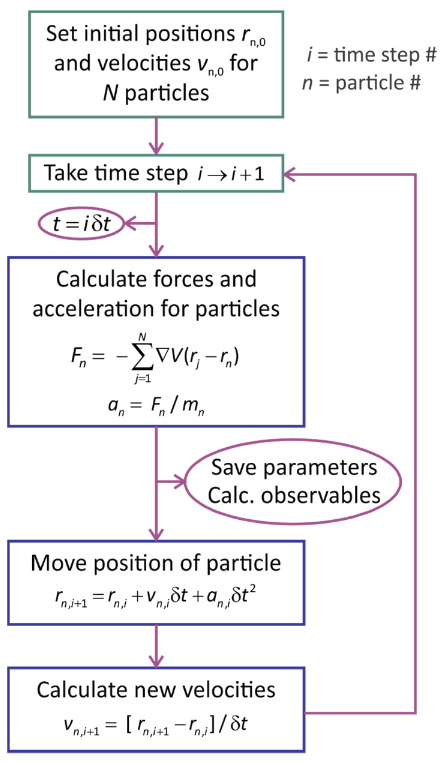

Una visión general de cómo integrar la ecuación de movimiento de Newton, dejando fuera muchos detalles importantes. Este esquema, a menudo utilizado en simulaciones MD, se denomina comúnmente integración Verlet.

1. Establecer posiciones iniciales r y velocidades v de partículas. Para las simulaciones de equilibrio, las velocidades se eligen de una distribución Maxwell—Boltzmann.
2. Dé pequeños pasos sucesivos en el tiempo δt, calculando las velocidades y posiciones de las partículas para el siguiente paso de tiempo.
   • En cada paso de tiempo calcular las fuerzas sobre cada partícula calculando el gradiente del potencial con respecto a r: F (r) =\(-\Delta V\) (r). La fuerza es proporcional a la aceleración a = F/m, donde m es la masa de la partícula.
   • Ahora propaga la posición de cada partícula n en el tiempo desde el paso de tiempo i hasta el paso de tiempo i + 1 como r _{^{n, i + 1}} = r _{n, i} + v _{n, i} δt + a _{n, i} δt ². Este es un buen punto para guardar información para el sistema en un momento determinado.
   • Calcular la nueva velocidad para cada partícula a partir de v _{n, i + 1} = [r _{n, i + 1} ‒ r _{n, i}] /δt.
3. Ahora, puede incrementar el paso de tiempo y repetir el paso iterativamente.

Dinámica Langevin

A partir de nuestra discusión sobre el movimiento browniano, la ecuación de Langevin es una ecuación de movimiento para una partícula que actúa bajo la influencia de un potencial fijo U, fricción y una fuerza aleatoria dependiente del tiempo. Escribirlo en una dimensión:

\[ ma= f_{\textrm{potential}}+f_{\textrm{friction}}+f{\textrm{random}}(t) \]

\[ m \frac{\partial^{2} x}{\partial t^{2}}=-\frac{\partial U}{\partial x}-\zeta \frac{\partial x}{\partial t}+f_{r}(t) \]

La fuerza aleatoria refleja las fluctuaciones térmicas de equilibrio que actúan sobre la partícula, y es la fuente de la fricción sobre la partícula. En el límite Markoviano, el coeficiente de fricción y la fuerza aleatoria f _r (t) se relacionan a través de una relación fluctuación-disipación:

\[\langle f_r(t)\rangle = 0 \]

\[\langle f_r(t)f_r(t_0)\rangle = 2ζ k_BT \delta (t-t_0) \]

Además, la constante de difusión es D = k _B T /, y la escala de tiempo para las correlaciones de pérdida de velocidad es\( \tau_c = \gamma-1 =\) m/. La ecuación de Langevin tiene límites de fricción altos y bajos. En el límite de fricción bajo (→0), la influencia de la fricción y la fuerza aleatoria es mínima, y el comportamiento está dominado por el movimiento inercial de la partícula. En el límite de fricción alto, el comportamiento de la partícula, al estar dominado por, es difusivo. El límite está definido por dos cualesquiera de las siguientes cuatro variables linealmente relacionadas:, D, T, y\(\langle f_r^2 \rangle \). El límite de fricción alto y bajo también se conoce como los límites de baja y alta temperatura:\( \langle f_r^2 \rangle / 2ζ = k_BT \).

Ejemplo: Trayectoria para una partícula sobre un potencial biestable de la dinámica Langevin