22.5: Funciones de correlación de tiempo

Funciones de correlación de tiempo

Las funciones de correlación temporal se utilizan comúnmente para caracterizar la dinámica de un proceso aleatorio (o estocástico). Si observamos el comportamiento de una variable interna A que describe el comportamiento de una molécula en equilibrio térmico, puede estar sujeta a fluctuaciones microscópicas.

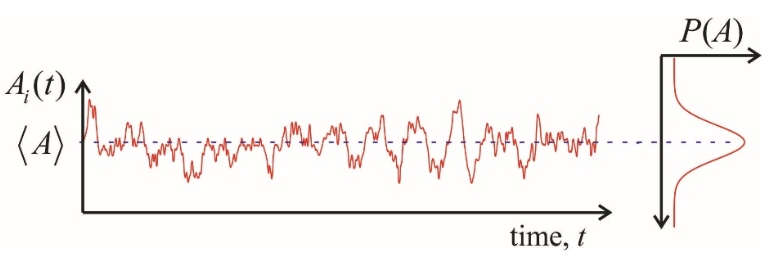
Si bien puede parecer poca información en esta ruidosa trayectoria, esta dinámica no es del todo aleatoria, ya que son consecuencia de interacciones dependientes del tiempo con el entorno. Podemos proporcionar una descripción estadística de las escalas de tiempo características y amplitudes a estos cambios comparando el valor de A en el tiempo t con el valor de A en un momento posterior t'. Definimos una función de correlación de tiempo como el producto de estos valores promediados sobre un conjunto de equilibrio:

\[C_{AA}(t-t') \equiv \langle A(t)A(t')\rangle \]

Las funciones de correlación no dependen del punto absoluto de observación (t y t'), sino del intervalo de tiempo entre observaciones (para procesos aleatorios estacionarios). Entonces, podemos definir el intervalo de tiempo\( \tau \equiv t-t'\), y expresar nuestra función como\(C_{AA}(\tau)\).

Podemos ver que cuando evaluamos C _AA a τ=0, obtenemos el valor cuadrático medio de\( A , \langle A^2 \rangle\). En tiempos largos, a medida que las fluctuaciones térmicas actúan para aleatorizar el sistema, los valores de A se vuelven descorrelacionados:\(\lim_{\tau\to\infty} C_{AA}(\tau)=\langle A\rangle ^2\). Por lo tanto, es común redefinir la función de correlación en términos de la desviación de la media

\[ \delta A=A-\langle A\rangle \]

\[ C_{\delta A\delta A}(t)=\langle \delta A(t)\delta A(0) \rangle = C_{AA}(t)-\langle A\rangle ^2 \]

Luego\(C_{\delta A \delta A}(0)\) da la varianza para el proceso aleatorio, y la función de correlación decae a cero como τ → ∞. La escala de tiempo característica para esta relajación es el tiempo de correlación,\(\tau_c\). que podemos obtener de

\[ \tau_c = \dfrac{1}{\langle \delta A^2 \rangle } \int_0^{\infty}dt \langle \delta A(t) \delta A(0)\rangle \]

La función de correlación clásica se puede obtener a partir de una distribución de probabilidad de equilibrio como

\[ C_{AA}(t-t')=\int \mathrm{d}p \int \mathrm{d}q A(p,q;t) A(p,q;t') P_{eq}(p,q) \]

En la práctica, la función de correlación se obtiene más comúnmente a partir de trayectorias calculándola como promedio de tiempo

\[C_{A A}(\tau)=\overline{A(\tau) A(0)}=\lim _{T \rightarrow \infty} \frac{1}{T} \int_{0}^{T} d t^{\prime} A_{i}\left(\tau+t^{\prime}\right) A_{i}\left(t^{\prime}\right)\]

Si el valor promedio de tiempo de C va a ser igual al valor promedio del conjunto de equilibrio de C, decimos que el sistema es ergódico.

Ejemplo: Función de Autocorrelación de Velocidad para Gas

Un gas diluido de moléculas tiene una distribución de velocidades Maxwell—Boltzmann, para lo cual nos enfocaremos en la componente de velocidad a lo largo de la\(\hat{x}\) dirección, x _v. Sabemos que la velocidad promedio es\(\langle v_x \rangle=0\). La función de correlación de velocidad es

\[c_{v_xv_x}(\tau)=\langle v_x(\tau)v_x(0)\rangle \nonumber\]

La energía traslacional promedio es\(\frac{1}{2}m\langle v_x^2 \rangle = k_BT/2 \), entonces

\[C_{v_xv_x}(0)=\langle v_x^2(0) \rangle = \dfrac{k_BT}{m} \nonumber \]

Para escalas de tiempo que son cortas en comparación con el tiempo promedio de colisión entre moléculas, la velocidad de cualquier molécula dada permanece constante y sin cambios, por lo que la función de correlación para la velocidad también no cambia a k _B T/m. Este régimen de no interacción corresponde al comportamiento de un gas ideal .

Para cualquier gas real, habrá colisiones que aleatorizan la dirección y velocidad de las moléculas, de manera que cualquier molécula durante un tiempo suficientemente largo tomará muestras de las diversas velocidades dentro de la distribución Maxwell—Boltzmann. A partir de la trayectoria de las velocidades x para una molécula dada podemos calcular\(C_{v_xv_x}(\tau)\) usando promedio de tiempo. La función de correlación caerá con un tiempo de correlación τc, que está relacionado con el tiempo medio entre colisiones. Después de suficientes colisiones, la correlación con la velocidad inicial se pierde y se\(C_{v_xv_x}(\tau)\) acerca\(\langle v_x^2 \rangle = 0 \). Finalmente, podemos determinar la constante de difusión para el gas, lo que relaciona el tiempo y el desplazamiento cuadrático medio de las moléculas:\(\langle x^2(t)\rangle = 2D_xt\). De\(D_x= \int_0^{\infty}dt\langle v_x(t)v_x(0)\rangle \) nosotros tenemos\(D_x = k_BT\tau_c/m\). En los fluidos viscosos\(\tau_c/m\) se llama la movilidad.

Calcular una función de correlación a partir de una trayectoria

Podemos evaluar la eq. (22.5.6) para una trayectoria discreta y finita en la que se nos da una serie de N observaciones de la variable dinámica A en puntos temporales igualmente separados t _i. La separación entre puntos de tiempo es t _i+1 ‒ t _i = δt, y la longitud de la trayectoria es T=N δt. Entonces tenemos

\[C_{AA} = \dfrac{1}{T} \sum_{i,j=1}^{N} \delta t A(t_i) A(t_j) = \dfrac{1}{N}\sum_{i,j=1}^NA_iA_j \]

donde\(A_i=A(t_i)\). Para que esto sea más útil queremos expresarlo como el intervalo de tiempo entre puntos\(\tau = t_j-t_i = (j-i)\delta t\), y el promedio sobre todos los posibles productos por pares de A separados por τ. Al definir un nuevo número entero n=j-i, podemos expresar el retraso como\(\tau = n\delta t\). Para un conjunto de datos finitos hay un número diferente de observaciones para promediar en cada intervalo de tiempo (n). Tenemos la mayor cantidad de productos por pares —N para ser precisos— cuando los puntos de tiempo son iguales (t _i = t _j). Solo tenemos un par de datos para el retardo máximo τ = T. Por lo tanto, el número de productos por pares para un retardo dado τ es N ‒ n. Así podemos escribir eq. (22.5.7) como

\[C_{AA} (\tau) = C(n) = \dfrac{1}{N-n}\sum_{i-1}^{N-n}A_{i+n}A_i \]

Obsérvese que esta expresión sólo se calculará para valores positivos de n, para los cuales t _j ≥ t _i.

Como ejemplo, considere el siguiente cálculo para las fluctuaciones en la intensidad de fluorescencia en un experimento de FCS. Esta trayectoria consta de 32000 mediciones consecutivas separadas por 44 μs, y se grafica como una desviación de la media δ A (t) = A (t) ‒ A.

La función de correlación obtenida de la ecuación (22.5.8) es

Podemos ver que la decadencia de la función de correlación se observa para retardos de tiempo de sub-ms. A partir de la eq. (22.5.4) encontramos que el tiempo de correlación es τ _C = 890 μs.