23.2: Teoría de Kramers

En nuestro tratamiento, el movimiento del reactivo sobre el estado de transición fue tratado como un grado de libertad transicional libre. Este movimiento balístico o inercial no es representativo de la dinámica en materia blanda a temperatura ambiente. La teoría de Kramers es el enfoque principal para describir el cruce de barreras difusivas. Representa la fricción y la agitación térmica que reducen la fracción de cruces de barrera exitosos. Nuevamente, las velocidades se obtienen del flujo sobre la barrera a lo largo de la coordenada de reacción, Ecuación (23.1).

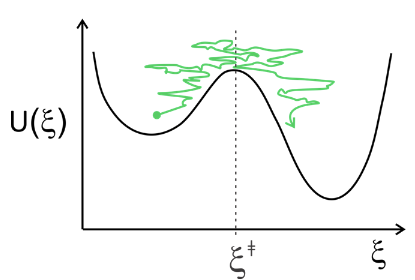
Un enfoque es tratar el cruce difusivo sobre la barrera en un potencial usando la ecuación de Smoluchowski. El flujo difusivo bajo influencia del potencial tiene dos contribuciones:

1. Gradiente de concentración\(dC/dξ\). Proporcional al coeficiente de difusión,\(D\).
2. Fuerza a partir del gradiente de potencial.

\[ J(\xi)=-D \frac{d C(\xi)}{d \xi}-\frac{C(\xi)}{\zeta} \frac{d U(\xi)}{d \xi} \nonumber\]

Como se discutió anteriormente\(ζ\) es el coeficiente de fricción y en una dimensión:

\[ \zeta=\frac{k_{B} T}{D} \nonumber\]

Escrito en términos de densidad de probabilidad\(P\)

\[\begin{align*} J &=D\left(-\frac{P}{k_{B} T} \frac{d U}{d \xi}-\frac{d P}{d \xi}\right) \\ &=-D e^{-U / k_{B} T} \frac{d}{d \xi}\left(P e^{U / k_{B} T}\right) \end{align*}\]

o

\[ J e^{U / k_{B} T}=-D \frac{d}{d \xi} P e^{U / k_{B} T} \]

Aquí hemos asumido que\(D\) y no\(ζ\) son funciones de\(ξ\).

La siguiente suposición importante de la teoría de Kramers es que podemos resolver para el flujo difusivo usando la aproximación de estado estacionario. Esto nos permite establecer:\(J\) = constante. Integrar a lo\(ξ\) largo de la barrera.

\[ \begin{align*} J \int_{a}^{b} e^{U / k_{B} T} d \xi * &=-D \int_{a}^{b} d P e^{U / k_{B} T} \\[4pt]  J \int_{a}^{b} e^{U(\xi) / k_{B} T} d \xi &=D\left\{P_{R} e^{U_{R} / k_{B} T}-P_{P} e^{U_{P} / k_{B} T}\right\} \end{align*}\]

\(P_i\)son las probabilidades de ocupar el\(R\) o\(P\) estado, y\(U_i\) son las energías de los\(P\) estados\(R\) y. El lado derecho de esta ecuación describe el flujo neto a través de la barrera.

Consideremos solo el flujo de\(R\longrightarrow P\):\( J_{R\longrightarrow P} \), que hacemos configurando\(P_P\longrightarrow 0\). Esto es solo un problema de escape de barrera. También como punto de referencia, nos fijamos\(U_R(ξ_R) = 0\).

\[ J_{R \rightarrow P}=\frac{D P_{R}}{\int_{a}^{b} e^{U(\xi) / k_{B} T} d \xi} \label{23.2.2}\]

El flujo es linealmente proporcional al coeficiente de difusión y a la probabilidad de estar en el estado reactivo. El flujo se reduce por un factor que describe la barrera energética a superar. Ahora evaluemos con una forma específica del potencial. La forma más sencilla es modelar\(U(ξ)\) con parábolas. El pozo reactivo viene dado por

\[ U_{R}=\frac{1}{2} m \omega_{R}^{2}\left(\xi-\xi_{R}\right)^{2} \label{23.2.3}\]

y nos fijamos\(\xi_R \longrightarrow 0\). La barrera es modelada por una parábola invertida centrada en el estado de transición con una altura de barrera para la reacción hacia adelante\(E_f\) y un ancho dado por la frecuencia de barrera\(ω_{bar}\):

\[ U_{\mathrm{bar}}=E_{f}-\frac{1}{2} m \omega_{\mathrm{bar}}^{2}\left(\xi-\xi^{‡}\right)^{2} \nonumber\]

En esencia se trata de tratar la evolución de la distribución de probabilidad como el movimiento de una partícula ficticia con masa\(m\).

Primero evaluamos el denominador en la Ecuación\ ref {23.2.2}. \(e^{U_{bar}/k_BT}\)es una densidad de probabilidad que alcanza su punto máximo\( \xi^‡\), por lo que cambiar los límites de la integral no afecta mucho a las cosas.

\[\int_{a}^{b} e^{U_{b a r} / k_{B} T} d \xi \approx \int_{-\infty}^{+\infty} d \xi \exp \left[-\frac{m \omega_{B}^{2}\left(\xi-\xi^{‡}\right)^{2}}{2 k_{B} T}\right]=\sqrt{\frac{2 \pi k_{B} T}{m \omega_{B}^{2}}} \nonumber\]

Entonces la Ecuación\ ref {23.2.2} se convierte

\[ J_{R \rightarrow P}=\omega_{\text {bar }} D \sqrt{\frac{m}{2 \pi k_{B} T}} e^{-E_{f} / k_{B} T} P_{R} \label{23.2.4}\]

A continuación, evaluemos\(P_R\). Para un pozo gaussiano en la Ecuación\ ref {23.2.3}, la densidad de probabilidad a lo largo\(ξ\) es\(P_R = e^{-U_{R} / k_{B} T}\):

\[ P_{R}(\xi)=\exp \left[-\frac{1}{2} m \omega_{R}^{2}\left(\xi-\xi_{R}\right)^{2} / k_{B} T\right] \nonumber\]

\[ P_{R} \approx \int_{-\infty}^{+\infty} P_{R}(\xi) d \xi=\omega_{R} \sqrt{\frac{m}{2 \pi k_{B} T}} \nonumber\]

Sustituyendo esto en la Ecuación\ ref {23.2.4} tenemos

\[ J_{R \rightarrow P}=\omega_{R} \omega_{b a r} D\left(\frac{m}{2 \pi k_{B} T}\right) e^{-E_{f} / k_{B} T} \nonumber\]

Usando la relación de Einstein\( D = k_BT/\zeta \), encontramos que el flujo directo escala inversamente con la fricción (o viscosidad).

\[ J_{R \rightarrow P}=\frac{\omega_{R}}{2 \pi} \frac{\omega_{b a r}}{\zeta} e^{-E_{f} / k_{B} T} \]

Además, el factor de\(m\) desaparece cuando el problema se expresa en coordenadas ponderadas en masa\(\omega_{\text {bar }}=\sqrt{m} \omega_{\text {bar }}\). Observe la similitud de la Ecuación (9) con la teoría del estado de transición. Si asociamos el periodo de la partícula en el pozo reactivo con la frecuencia de cruce de barrera,

\[ \frac{\omega_{R}}{2 \pi} \Rightarrow v=\frac{k_{B} T}{h} \nonumber\]

entonces también podemos encontrar que tenemos una expresión para el coeficiente de transmisión en este modelo:

\[ k_{diff}=\kappa_{diff} k_{TST} \nonumber\]

\[ \kappa_{diff}=\dfrac{\omega_{bar}}{\zeta}\ll 1 \nonumber\]

Esta es la velocidad de reacción en el límite de amortiguación fuerte, o difusivo. Hendrik Kramers realmente resolvió un problema más general basado en la ecuación de Fokker—Planck que describía amortiguación intermedia a fuerte. La velocidad de reacción se describió como

\[ k_{Kr}=\kappa_{Kr} k_{TST} \nonumber\]

\[\kappa_{K r}=\frac{1}{\omega_{b a r}}\left(-\frac{\zeta}{2}+\sqrt{\frac{\zeta^{2}}{4}+\omega_{b a r}^{2}}\right) \nonumber\]

\[ \zeta=\frac{1}{m k_{B} T} \int_{0}^{\infty} d t\langle\xi(0) \xi(t)\rangle \nonumber\]

Esto muestra un cruce en el comportamiento entre el comportamiento de amortiguación fuerte (o difusivo) descrito anteriormente y un régimen de amortiguación intermedio:

• Fuerte amortiguación/fricción:\(\zeta \longrightarrow \infty\)\(\kappa_{Kr}\longrightarrow\dfrac{\omega_{bar}}{\zeta} \nonumber\)
• Amortiguación intermedia:\(\zeta <<2\omega_B\)\(\kappa_{Kr}\longrightarrow 1\) y\(k_{Kr}\longrightarrow k_{TST} \nonumber\)

En el límite de fricción débil, Kramers argumentó que la velocidad de reacción se escaló como

\[k_{\text {weak }} \sim \zeta k_{T S T} \nonumber\]

Es decir, si no tuvieras fricción alguna, la partícula simplemente se movería de un lado a otro entre el reactivo y el estado del producto sin comprometerse con un pozo en particular. Necesitas algo de disipación para relajarte irreversiblemente en el pozo del producto. En base a esto se espera una fricción óptima que maximice\(κ\), lo que equilibra la necesidad de cierta disipación pero sin tanto que el cruce de barreras sea sumamente raro. Esta “rotación de Kramers” es capturada por la fórmula de interpolación

\[\kappa^{-1}=\kappa_{K r}^{-1}+\kappa_{\text {weak }}^{-1} \nonumber\]