1.2: Índices Miller (hkl)
- Page ID
- 69249
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La orientación de una superficie o un plano cristalino puede definirse considerando cómo el plano (o de hecho cualquier plano paralelo) intersecta los ejes cristalográficos principales del sólido. La aplicación de un conjunto de reglas conduce a la asignación de los índices Miller (hkl), que son un conjunto de números que cuantifican las intercepciones y así pueden ser utilizados para identificar de manera única el plano o superficie.
El siguiente tratamiento del procedimiento utilizado para asignar los índices Miller es uno simplificado (puede ser mejor si simplemente lo considera como una “receta”) y solo se considerará un sistema de cristal cúbico (uno que tenga una celda unitaria cúbica con dimensiones a x a x a) .
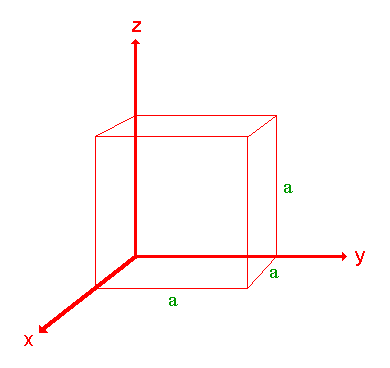
El procedimiento se ilustra más fácilmente usando un ejemplo por lo que primero consideraremos la siguiente superficie/plano:
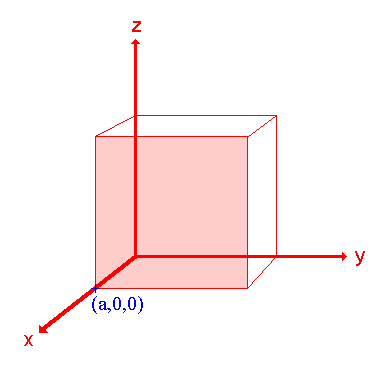
Paso 1: Identificar las intercepciones en los ejes x, y y z.
En este caso la intercepción en el eje x está en x = a (en el punto (a ,0,0)), pero la superficie es paralela a los ejes y - y z - estrictamente por lo tanto no hay intercepción en estos dos ejes pero consideraremos que la intercepción está en infinito ( ∞) para el caso especial donde el plano es paralelo a un eje. Las intercepciones en los ejes x -, y - y z son así
Intercepciones: a, ∞, ∞
Paso 2: Especificar las intercepciones en coordenadas fraccionarias
Las coordenadas se convierten en coordenadas fraccionarias dividiendo por la dimensión celular respectiva; por ejemplo, un punto (x, y, z) en una celda unitaria de dimensiones a x b x c tiene coordenadas fraccionarias de (x/a , y/b, z/c). En el caso de una celda unitaria cúbica, cada coordenada simplemente se dividirá por la constante de celda cúbica, a. Esto da
Intercepciones fraccionarias: a/a, ∞/a, ∞/a es decir , 1, ∞, ∞
Paso 3: Toma los recíprocos de las intercepciones fraccionarias
Esta manipulación final genera los índices Miller que (por convención) deberían especificarse entonces sin estar separados por comas u otros símbolos. Los índices Miller también están encerrados entre corchetes estándar (...) cuando se está especificando una superficie única como la que se considera aquí.
Los recíprocos de 1 y ∞ son 1 y 0 respectivamente, cediendo así
Índices Miller: (100)
Entonces la superficie/plano ilustrado es el plano (100) del cristal cúbico.
Otros Ejemplos
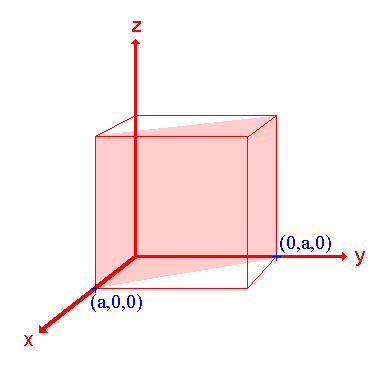
1. La superficie (110)
|
|
Asignación Intercepciones: a, a, ∞ Intercepciones fraccionarias: 1, 1, ∞ Índices Miller: (110) |
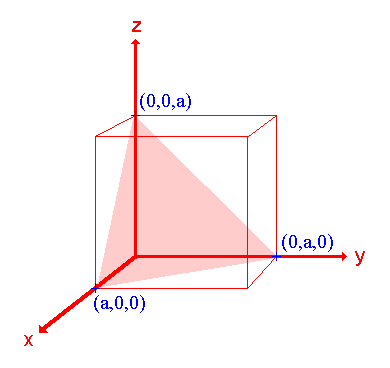
2. La superficie (111)
|
|
Asignación Intercepciones: a, a, a Intercepciones fraccionarias: 1, 1, 1 Índices Miller: (111) |
Las superficies (100), (110) y (111) consideradas anteriormente son las llamadas superficies de índice bajo de un sistema de cristal cúbico (la “baja” se refiere a que los índices Miller son números pequeños - 0 o 1 en este caso). Estas superficies tienen una importancia particular pero hay un número infinito de otros planos que pueden definirse usando la notación de índice Miller. Basta con mirar a una más...
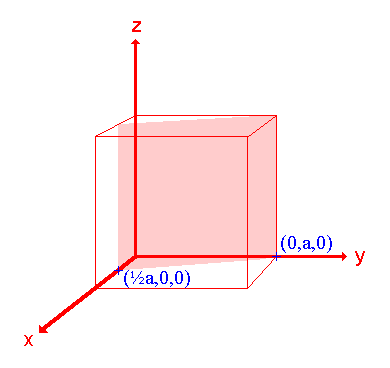
3. La superficie (210)
|
|
Asignación Intercepciones: ½ a, a, ∞ Intercepciones fraccionarias: ½, 1, ∞ Índices Miller: (210) |
Notas adicionales:
- en algunos casos los índices Miller se multiplican o dividen mejor por un número común para simplificarlos, por ejemplo, eliminando un factor común. Esta operación de multiplicación simplemente genera un plano paralelo que se encuentra a una distancia diferente del origen de la celda unitaria particular que se está considerando. e.g. (200) se transforma a (100) dividiendo por 2.
- si alguna de las intercepciones está en valores negativos en los ejes, entonces el signo negativo se trasladará a los índices Miller; en tales casos el signo negativo se denota realmente sobregolpeando el número relevante. e.g. (00 -1) se denota por

- en el sistema de cristal hcp hay cuatro ejes principales; esto lleva a cuatro índices Miller, por ejemplo, puede ver artículos que hacen referencia a una superficie hcp (0001). Cabe señalar, sin embargo, que las intercepciones en los tres primeros ejes están necesariamente relacionadas y no completamente independientes; en consecuencia, los valores de los tres primeros índices de Miller también están vinculados por una simple relación matemática.
¿Qué son las superficies equivalentes a simetría?
En el siguiente diagrama las tres superficies resaltadas están relacionadas por los elementos de simetría del cristal cúbico, son totalmente equivalentes.
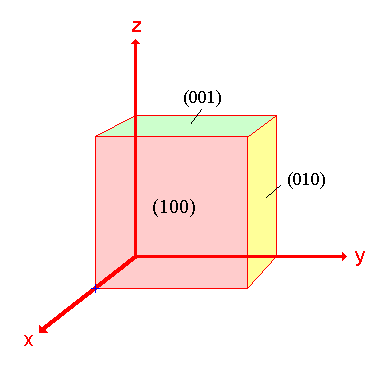
De hecho hay un total de 6 caras relacionadas por los elementos de simetría y equivalentes a la (100) superficie - cualquier superficie perteneciente a este conjunto de superficies relacionadas con la simetría puede ser denotada por la notación más general {100} donde los índices de Miller de una de las superficies están encerrados en corchetes rizados.
Nota importante final: en el sistema cúbico el plano (hkl) y el vector [hkl], definidos de manera normal con respecto al origen, son normales entre sí pero esta característica es única para el sistema de cristales cúbicos y no aplica a sistemas cristalinos de menor simetría.