5.1: Espectroscopia de correlación bidimensional

Última actualización
Guardar como PDF

Page ID: 73667

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

¿Qué es la espectroscopia bidimensional? Este es un método que describirá las correlaciones subyacentes entre dos características espectrales. Nuestro examen de experimentos de bomba-sonda indica que la respuesta de tercer orden informa sobre la correlación entre diferentes características espectrales. Veamos esto con más detalle utilizando como ejemplo un sistema con dos estados excitados, para lo cual el espectro de absorción muestra dos características espectrales en\(\omega_{ba}\) y\(\omega_{ca}\).

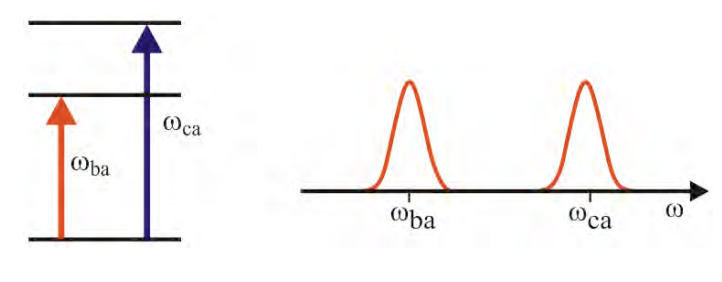
Imagine un experimento de doble resonancia (bomba-sonda) en el que elegimos una frecuencia de excitación sintonizable\(\omega_{pump}\), y para cada frecuencia de bomba medimos los cambios en el espectro de absorción en función de\(\omega_{probe}\). En términos generales, esperamos que la excitación resonante induzca un cambio de absorbancia.

La pregunta es: ¿qué observamos si bombeamos\(\omega_{ba}\) y sondamos en\(\omega_{ca}\)? Si no pasa nada, entonces podemos concluir que microscópicamente, no hay interacción entre los grados de libertad que dan lugar a las transiciones ba y ca. Sin embargo, un cambio de absorbancia en\(\omega_{ca}\) indica que de alguna manera la excitación de\(\omega_{ba}\) está correlacionada con\(\omega_{ca}\). Microscópicamente, existe un acoplamiento o conversión química que permite que la energía depositada fluya entre las coordenadas. Alternativamente, podemos decir que las transiciones observadas ocurren entre estados propios cuyo carácter y energía codifican interacciones moleculares entre los grados de libertad acoplados (aquí\(\beta\) y\(\chi\)):

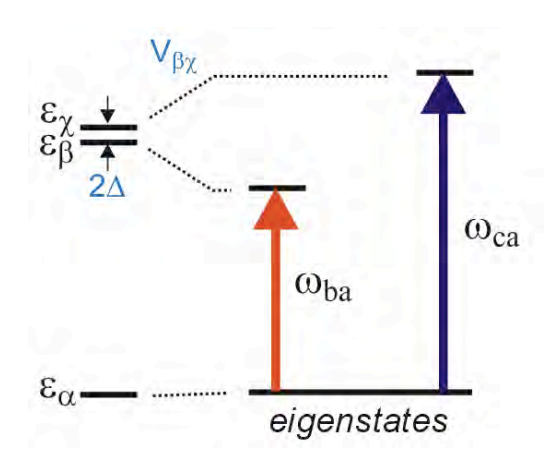
Ahora imagine que realiza este experimento de doble resonancia midiendo el cambio en la absorción para todos los valores posibles de\(\omega_{pump}\) y\(\omega_{probe}\), y graficarlos como una gráfica de contorno bidimensional: ¹

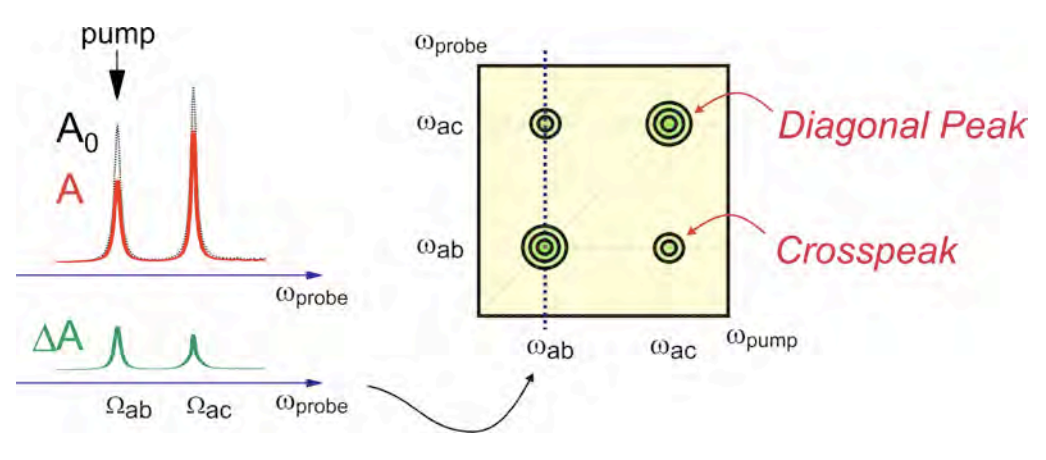
Se trata de un espectro bidimensional que informa sobre la correlación de las características espectrales observadas en el espectro de absorción. Los picos diagonales reflejan el caso donde se bombea y sonda la misma resonancia. Los picos cruzados indican una correlación cruzada que surge de bombear una característica y observar un cambio en la otra. Los principios de la espectroscopia de correlación en esta forma se desarrollaron inicialmente en el área de resonancia magnética, pero están encontrando un uso creciente en las áreas de espectroscopia óptica e infrarroja.

Analogías de doble resonancia como estas ilustran el poder de un espectro bidimensional para visualizar las interacciones moleculares en un sistema complejo con muchos grados de libertad. De igual manera, podemos ver cómo un espectro 2D puede separar componentes de una mezcla a través de la presencia o ausencia de picos cruzados.

Además, queda claro cómo una forma de línea no homogénea se puede descomponer en la distribución de configuraciones, y la dinámica subyacente dentro del conjunto. Tomar una forma de línea no homogénea con ancho\(\Delta\) y frecuencia media\(\langle\omega_{ab}\rangle\), que se compone de una distribución de transiciones homogéneas de ancho\(\Gamma\). Ahora someteremos al sistema a la misma excitación de banda estrecha seguida de sondear la absorción diferencial\(\Delta A\) en todas las frecuencias de la sonda.

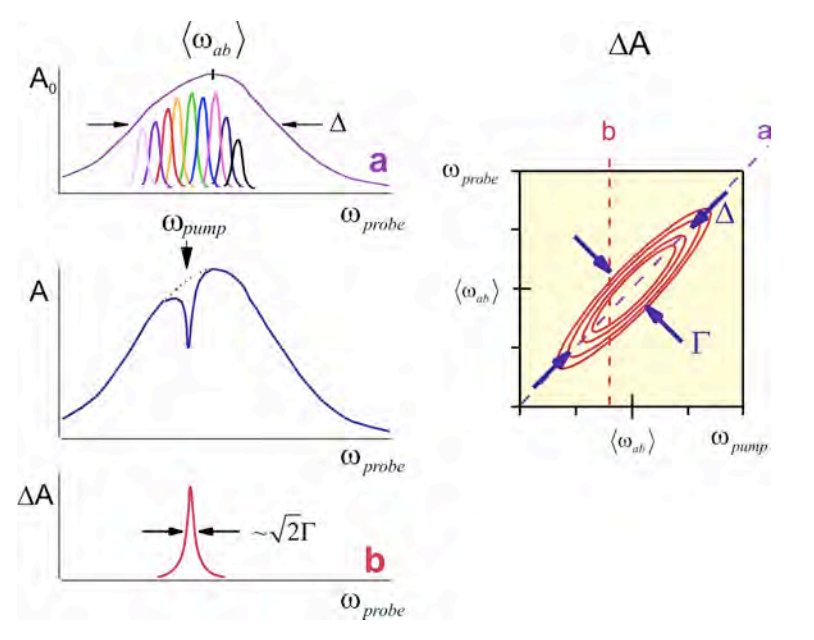
Aquí observamos que los contornos de un lineshape bidimensional reportan sobre el ensanchamiento no homogéneo. Observamos que la forma de línea es alargada a lo largo del eje diagonal\((\omega_1=\omega_3)\). El ancho de línea diagonal está relacionado con el ancho no homogéneo Δ mientras que el ancho antidiagonal\(\left[\omega_1+\omega_3=\langle\omega_{ab}\rangle/2\right]\) está determinado por el ancho de línea homogéneo\(\Gamma\).

1. Aquí utilizamos la convención de reglas de la derecha para los ejes de frecuencia, en la que la frecuencia de bombeo o excitación está en el eje horizontal y la frecuencia de sonda o detección está en el eje vertical. Se están utilizando diferentes convenciones, lo que sí genera confusión. Observamos que las primeras presentaciones de espectros bidimensionales en el caso de espectros 2D Raman e IR 2D utilizaron una convención RHR, mientras que las primeras mediciones electrónicas de RMN 2D y 2D utilizaron la convención LHR.