7.3: Resolviendo la ecuación de Schrödinger del rotor rígido
- Page ID
- 71212
Para resolver la ecuación de Schrödinger para el rotor rígido, separaremos las variables y formaremos ecuaciones de una sola variable que se pueden resolver de forma independiente. Sólo\(\varphi\) se requieren dos variables\(\theta\) y en el modelo de rotor rígido debido a que la longitud de unión\(r\),, se toma como la constante\(r_0\). Primero escribimos las funciones de onda rígidas del rotor como el producto de una función theta dependiendo solo de\(\theta\) y una\(\phi\) función dependiendo solo de\(\varphi\)
\[ \psi (\theta , \varphi ) = \Theta (\theta ) \Phi (\varphi) \label{7-12}\]
Luego sustituimos la función de onda del producto y la hamiltoniana escrita en coordenadas esféricas en la Ecuación de Schrödinger\ ref {7-13}:
\[\hat {H} \psi (\theta , \varphi ) = E \psi (\theta , \varphi ) \label{7-13}\]
para obtener
\[ -\dfrac {\hbar ^2}{2\mu r^2_0} \left [ \dfrac {\partial}{\partial r_0} r^2_0 \dfrac {\partial}{\partial r_0} + \dfrac {1}{\sin \theta} \dfrac {\partial}{\partial \theta } \sin \theta \dfrac {\partial}{\partial \theta } + \dfrac {1}{\sin ^2 \theta} \dfrac {\partial ^2}{\partial \varphi ^2} \right ] \Theta (\theta ) \Phi (\varphi) = E \Theta (\theta) \Phi (\varphi) \label {7-14}\]
Dado que\(r = r_0\) es constante para el rotor rígido y no aparece como una variable en las funciones, las derivadas parciales con respecto a\(r\) son cero; es decir, las funciones no cambian con respecto a\(r\). También podemos sustituir el símbolo\(I\) por el momento de inercia,\(\mu r^2_0\) en el denominador del lado izquierdo de la Ecuación\ ref {7-14}, para dar
\[-\dfrac {\hbar ^2}{2I} \left [ \dfrac {1}{\sin \theta} \dfrac {\partial}{\partial \theta } \sin \theta \dfrac {\partial}{\partial \theta } + \dfrac {1}{\sin ^2 \theta} \dfrac {\partial ^2}{\partial \varphi ^2}\right ] \Theta (\theta ) \Phi (\varphi) = E \Theta (\theta) \Phi (\varphi) \label{7-15}\]
Para iniciar el proceso de separación de las variables en la Ecuación\ ref {7-15}, multiplique cada lado de la ecuación por\(\dfrac {2I}{\hbar ^2}\) y\(\dfrac {-\sin ^ \theta}{\Theta (\theta) \Phi (\varphi)} \) para dar
\[\dfrac {1}{\Theta (\theta) \psi (\varphi)} \left [ \sin \theta \dfrac {\partial}{\partial \theta } \sin \theta \dfrac {\partial}{\partial \theta } + \dfrac {\partial ^2}{\partial \varphi ^2}\right ] \Theta (\theta ) \Phi (\varphi) = \dfrac {-2IE \sin ^2 \theta}{\hbar ^2} \label {7-16}\]
Simplifique la apariencia del lado derecho de la ecuación\ ref {7-16} definiendo un parámetro\(\lambda\):
\[ \lambda = \dfrac {2IE}{\hbar ^2} \label{7-17}\]
Tenga en cuenta que esto no\(\lambda\) tiene conexión con una longitud de onda; simplemente se está utilizando como símbolo algebraico para la combinación de constantes que se muestra en la Ecuación\ ref {7-17}.
Insertar\(\lambda\), evaluar derivadas parciales y reorganizar la ecuación\ ref {7-16} produce
\[\dfrac {1}{\Theta (\theta)} \left [ \sin \theta \dfrac {\partial}{\partial \theta } \left (\sin \theta \dfrac {\partial}{\partial \theta } \right ) \Theta (\theta) + \left ( \lambda \sin ^2 \theta \right ) \Theta (\theta) \right ] = - \dfrac {1}{\Phi (\varphi)} \dfrac {\partial ^2}{\partial \varphi ^2} \Phi (\varphi) \label {7-18}\]
Ejercicio\(\PageIndex{1}\)
Llevar a cabo los pasos que conducen de la Ecuación\ ref {7-16} a la Ecuación\ ref {7-18}. Tenga en cuenta que, si no\(y\) es una función de\(x\),
\[ \dfrac {dy}{dx} = y \dfrac {d}{dx}\]
La ecuación\ ref {7-18} dice que la función de la izquierda, dependiendo solo de la variable\(\theta\), siempre es igual a la función de la derecha, dependiendo solo de la variable\(\varphi\), para todos los valores de\(\theta\) y\(\varphi\). La única forma en que dos funciones diferentes de variables independientes pueden ser iguales para todos los valores de las variables es si ambas funciones son iguales a una constante (revisión de separación de variables). A esto lo llamamos constante\(m^2\) porque pronto necesitaremos la raíz cuadrada de la misma. Las dos ecuaciones diferenciales a resolver son la\(\theta\) ecuación -ecuación
\[\sin \theta \dfrac {d}{d \theta} \left ( \sin \theta \dfrac {d}{d \theta} \right ) \Theta (\theta ) + \left ( \lambda \sin ^2 \theta - m^2 \right ) \Theta (\theta ) = 0 \label {7-19}\]
y la\(\varphi\) ecuación -
\[ \dfrac {d^2}{d \varphi ^2} \Phi (\varphi ) + m^2 \Phi (\varphi) = 0 \label {7-20}\]
Las derivadas parciales han sido reemplazadas por derivadas totales porque en cada ecuación solo está involucrada una sola variable.
Ejercicio\(\PageIndex{2}\)
Mostrar cómo se obtienen las Ecuaciones\ ref {7-19} y\ ref {7-20} de la Ecuación\ ref {7-18}.
La\(\varphi\) ecuación -es similar a la ecuación de Schrödinger para la partícula libre. Como ya resolvimos esta ecuación diferencial en el Capítulo 5, inmediatamente escribimos las soluciones:
\[ \Phi _m (\varphi) = N e^{\pm im \varphi} \label {7-21}\]
Ejercicio\(\PageIndex{3}\)
Sustituye la Ecuación\ ref {7-21} en la Ecuación\ ref {7-20} para mostrar que es una solución a esa ecuación diferencial.
La condición de normalización, Ecuación\ ref {7-22}, se utiliza para encontrar un valor para\(N\) que satisfaga la Ecuación\ ref {7-21}.
\[ \int \limits ^{2 \pi} _0 \Phi ^*(\varphi) \Phi (\varphi) d \varphi = 1 \label {7-22}\]
El rango de la integral es solo de\(0\) a\(2π\) porque el ángulo\(\varphi\) especifica la posición del eje internuclear en relación con el eje x del sistema de coordenadas y los ángulos mayores que\(2π\) no especifican nuevas posiciones adicionales.
Ejercicio\(\PageIndex{4}\)
Utilice la condición de normalización, Ecuación\ ref {7-21} para mostrar que
\[N = (2π)-\dfrac{1}{2}.\]
Los valores para\(m\) se encuentran usando una condición de límite cíclico. La condición de límite cíclico significa que desde\(\varphi\) y\(\varphi + 2\varphi \) se refieren al mismo punto en el espacio tridimensional,\(\Phi (\varphi)\) debe ser igual\(\Phi (\varphi + 2 \varphi )\), i.e.
\[e^{im\varphi} = e^{im (\varphi + 2\pi)}\]
\[= e^{im\varphi} e^{im2\pi} \label {7-23}\]
Para que la igualdad en la Ecuación\(\ref{7-23}\) se mantenga,\(e^{im2\pi}\) debe ser igual a 1, lo cual es cierto sólo cuando
\[m = \cdots , -3, -2, -1, 0, 1, 2, 3, \cdots \label {7-24}\]
En otras palabras, m puede ser igual a cualquier entero positivo o negativo o cero.
Ejercicio\(\PageIndex{5}\)
Usa la Fórmula de Euler para mostrar que\(e^{im2π}\) es igual a 1 para\(m\) igual a cero o cualquier entero positivo o negativo.
Así, la\(Φ\) función es
\[\Phi _m (\varphi ) = (2\pi) ^{-1/2} e^{\pm im\varphi} \label {7-25}\]
\[ \text { with } m = 0, \pm 1, \pm 2, \cdots\]
Encontrar las\(\Theta (\theta)\) funciones que son soluciones a la\(\theta\) ecuación -ecuación, Ecuación\ ref {7-19}, es un proceso más complicado. Se encuentra que las soluciones son un conjunto de series de potencia llamadas Funciones Legendre Asociadas, que son series de potencia de funciones trigonométricas, es decir, productos y potencias de funciones sinusoidales y cosenoidales. Las\(\Theta (\theta)\) funciones, junto con sus constantes de normalización, se muestran en la tercera columna de Table\(\PageIndex{1}\).
| m | J | \(\Theta ^m_J (\theta)\) | \(\Phi (\varphi)\) | \(Y^m_J (\theta , \varphi)\) |
|---|---|---|---|---|
| 0 | 0 | \ (\ Theta ^m_J (\ theta)\)” style="vertical-align:middle; ">\(\dfrac {1}{\sqrt {2}}\) | \ (\ Phi (\ varphi)\)” style="vertical-align:middle; ">\(\dfrac {1}{\sqrt {2 \pi}}\) | \ (y^m_j (\ theta,\ varphi)\)” style="vertical-align:middle; ">\(\dfrac {1}{\sqrt {4 \pi}}\) |
| 0 | 1 | \ (\ Theta ^m_J (\ theta)\)” style="vertical-align:middle; ">\(\sqrt {\dfrac {3}{2}}\cos \theta\) | \ (\ Phi (\ varphi)\)” style="vertical-align:middle; ">\(\dfrac {1}{\sqrt {2 \pi}}\) | \ (y^m_j (\ theta,\ varphi)\)” style="vertical-align:middle; ">\(\sqrt {\dfrac {3}{4 \pi}}\cos \theta\) |
| 1 | 1 | \ (\ Theta ^m_J (\ theta)\)” style="vertical-align:middle; ">\(\sqrt {\dfrac {3}{4}}\sin \theta\) | \ (\ Phi (\ varphi)\)” style="vertical-align:middle; ">\(\dfrac {1}{\sqrt {2 \pi}}e^{i \varphi}\) | \ (y^m_j (\ theta,\ varphi)\)” style="vertical-align:middle; ">\(\sqrt {\dfrac {3}{8 \pi}}\sin \theta e^{i \varphi}\) |
| -1 | 1 | \ (\ Theta ^m_J (\ theta)\)” style="vertical-align:middle; ">\(\sqrt {\dfrac {3}{4}}\sin \theta\) | \ (\ Phi (\ varphi)\)” style="vertical-align:middle; ">\(\dfrac {1}{\sqrt {2 \pi}}e^{-i\varphi}\) | \ (y^m_j (\ theta,\ varphi)\)” style="vertical-align:middle; ">\(\sqrt {\dfrac {3}{8 \pi}}\sin \theta e^{-i \varphi}\) |
| 0 | 2 | \ (\ Theta ^m_J (\ theta)\)” style="vertical-align:middle; ">\(\sqrt {\dfrac {5}{8}}(3\cos ^2 \theta - 1)\) | \ (\ Phi (\ varphi)\)” style="vertical-align:middle; ">\(\dfrac {1}{\sqrt {2 \pi}}\) | \ (y^m_j (\ theta,\ varphi)\)” style="vertical-align:middle; ">\(\sqrt {\dfrac {5}{16\pi}}(3\cos ^2 \theta - 1)\) |
| 1 | 2 | \ (\ Theta ^m_J (\ theta)\)” style="vertical-align:middle; ">\(\sqrt {\dfrac {15}{4}} \sin \theta \cos \theta \) | \ (\ Phi (\ varphi)\)” style="vertical-align:middle; ">\(\dfrac {1}{\sqrt {2 \pi}}e^{i \varphi}\) | \ (y^m_j (\ theta,\ varphi)\)” style="vertical-align:middle; ">\(\sqrt {\dfrac {15}{8\pi}} \sin \theta \cos \theta e^{i\varphi}\) |
| -1 | 2 | \ (\ Theta ^m_J (\ theta)\)” style="vertical-align:middle; ">\(\sqrt {\dfrac {15}{4}} \sin \theta \cos \theta \) | \ (\ Phi (\ varphi)\)” style="vertical-align:middle; ">\(\dfrac {1}{\sqrt {2 \pi}}e^{-i\varphi}\) | \ (y^m_j (\ theta,\ varphi)\)” style="vertical-align:middle; ">\(\sqrt {\dfrac {15}{8\pi}} \sin \theta \cos \theta e^{-i\varphi}\) |
| 2 | 2 | \ (\ Theta ^m_J (\ theta)\)” style="vertical-align:middle; ">\(\sqrt {\dfrac {15}{16}} \sin ^2 \theta \) | \ (\ Phi (\ varphi)\)” style="vertical-align:middle; ">\(\dfrac {1}{\sqrt {2 \pi}}e^{2i\varphi}\) | \ (y^m_j (\ theta,\ varphi)\)” style="vertical-align:middle; ">\(\sqrt {\dfrac {15}{32\pi}} \sin ^2 \theta e^{2i\varphi} \) |
| -2 | 2 | \ (\ Theta ^m_J (\ theta)\)” style="vertical-align:middle; ">\(\sqrt {\dfrac {15}{16}} \sin ^2 \theta \) | \ (\ Phi (\ varphi)\)” style="vertical-align:middle; ">\(\dfrac {1}{\sqrt {2 \pi}}e^{2i\varphi}\) | \ (y^m_j (\ theta,\ varphi)\)” style="vertical-align:middle; ">\(\sqrt {\dfrac {15}{32\pi}} \sin ^2 \theta e^{-2i\varphi} \) |
La solución a la\(\theta\) ecuación requiere que\(λ\) en la Ecuación\ ref {7-18} esté dada por
\[\lambda = J (J + 1) \label {7-26}\]
donde
\[ J \ge |m| \label {7-27}\]
\(J\)puede ser 0 o cualquier entero positivo mayor o igual a m. Cada par de valores para los números cuánticos,\(J\) y\(m\), identifica un estado rotacional y una función de onda. Para mayor claridad al recordar que\(J\) controla los valores permitidos de\(m\), a menudo\(m\) se conoce como\(m_J\), y ahora usaremos esa notación.
La combinación de Ecuaciones\ ref {7-17} y\ ref {7-26} revela que la energía de este sistema está cuantificada.
\[ E = \dfrac {\hbar ^2 \lambda}{2I} = J(J + 1) \dfrac {\hbar ^2}{2I} \label {7-28}\]
Ejercicio\(\PageIndex{6}\)
Calcular los niveles de energía para una molécula giratoria para J = 0 a J = 5 usando unidades de\(\dfrac {\hbar ^2}{2I}\).
Usando la ecuación\ ref {7-28}, puedes construir un diagrama de nivel de energía rotacional. Para simplificar, use unidades de energía de\(\dfrac {\hbar ^2}{2I}\). El estado energético más bajo tiene\(J = 0\) y\(m_J = 0\). Este estado tiene una energía\(E_0 = 0\). Solo hay un estado con esta energía, es decir, un conjunto de números cuánticos, una función de onda y un conjunto de propiedades para la molécula.
El siguiente nivel de energía es\(J = l\) con energía\(\dfrac {2\hbar ^2}{2I}\). Hay tres estados con esta energía porque\(m_J\) puede ser igual a +1, 0 o ‑1. Estos diferentes estados corresponden a diferentes orientaciones de la molécula giratoria en el espacio. Estos estados se discuten en detalle en las Secciones 7.3 y 7.4. Se dice que los estados con la misma energía son degenerados. La degeneración de un nivel energético es el número de estados con esa energía. La degeneración del nivel\(J = l\) energético es de 3 porque hay tres estados con la energía\(\dfrac {2\hbar ^2}{2I}\).
El siguiente nivel de energía es para\(J = 2\). La energía es\(\dfrac {6\hbar ^2}{2I}\), y hay cinco estados con esta energía correspondiente a\(m_J = +2, +1, 0, ‑1, ‑2\). La degeneración del nivel energético es de cinco. Tenga en cuenta que la separación entre los niveles de energía aumenta a medida que aumenta J. También hay que señalar que la degeneración aumenta. La degeneración siempre se\(2J+1\) debe a que\(m_J\) va desde\(+J\) hasta\(‑J\) en pasos enteros, incluyendo 0.
Ejercicio\(\PageIndex{7}\)
\(J = 0\)Para\(J = 5\), identificar la degeneración de cada nivel de energía y los valores del número cuántico mJ que van con cada valor del número\(J\) cuántico. Construya un diagrama de nivel de energía rotacional (consulte Dibujo de diagramas de nivel de energía) incluyendo\(J\) = 0 a 5. Etiquetar cada nivel con los valores apropiados para los números cuánticos J y\(m_J\). Describir cómo el espaciamiento entre niveles varía con el aumento\(J\).
Una función de onda que es una solución a la ecuación de Schrödinger del rotor rígido (definida en la Ecuación\ ref {7-12}) puede escribirse como una sola función Y\(\theta, \varphi)\), que se denomina función armónica esférica.
\[ Y^{m_J} _J (\theta , \varphi ) = \Theta ^{|m_J|}_J (\theta) \Phi _{m_J} (\varphi) \label {7-29}\]
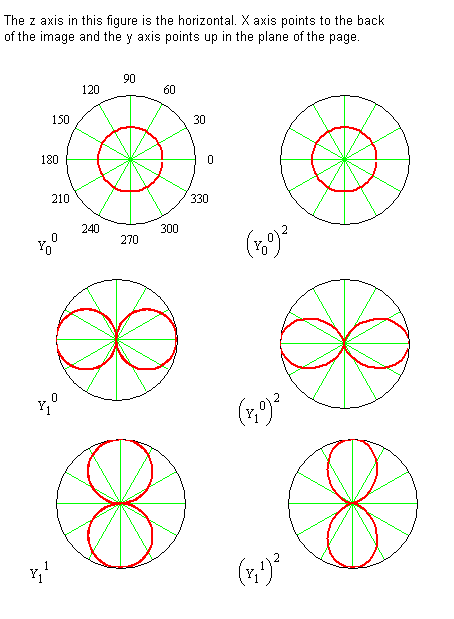
La función de onda armónica esférica está etiquetada con mJ y J porque su forma funcional depende de ambos números cuánticos. Estas funciones se tabulan arriba para\(J = 0\) a través\(J = 2\) y para\(J = 3\) en Tabla\(\PageIndex{1}\) Las gráficas de algunas de las\(\theta\) -funciones se muestran en la Figura\(\PageIndex{1}\).
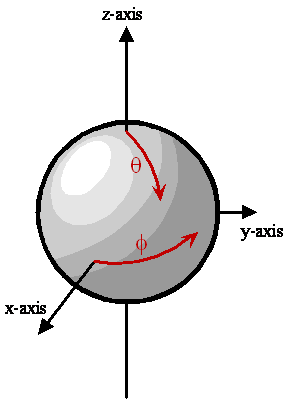
El espacio bidimensional para un rotor rígido se define como la superficie de una esfera de radio\(r_0\), como se muestra en la Figura\(\PageIndex{2}\).
La probabilidad de encontrar el eje internuclear en coordenadas específicas\(\theta _0\) y\(\varphi _0\) dentro de un área infinitesimal\(ds\) en esta superficie curva viene dada por
\[ Pr \left [ \theta _0, \varphi _0 \right ] = Y^{m_{J*}}_J (\theta _0, \varphi _0) Y^{m_J}_J (\theta _0, \varphi _0) ds \label {7-30}\]
donde el elemento de área ds está centrado en\(\theta _0\) y\(\varphi _0\). El cuadrado absoluto (o módulo cuadrado) de la función ondulada del rotor rígido\(Y^{m_{J*}}_J (\theta, \varphi) Y^{m_J}_J (\theta, \varphi) \) da la densidad de probabilidad para encontrar el eje internuclear orientado\(\theta\) al eje z y\(\varphi\) al eje x, y en coordenadas esféricas el elemento de área utilizado para integrar\(\theta\) y\(\varphi\) es
\[ds = \sin \theta d \theta d \varphi \label {7-31}\]
Ejercicio\(\PageIndex{8}\)
Utilice el cálculo para evaluar la probabilidad de encontrar el eje internuclear de una molécula descrita por la\(J = 1\) función de\(m_J = 0\) onda en algún lugar de la región definida por un rango\(\theta\) de 0° a 45°, y un rango de adentro de 0° a 90°. Tenga en cuenta que se necesitará una doble integral. Esboce esta región como un área sombreada en la Figura\(\PageIndex{1}\).
Considere la significancia de la función de densidad de probabilidad examinando la función de onda J = 1, mJ = 0. El armónico esférico para este caso es
\[ Y^0_1 = \left ( \dfrac {3}{4 \pi} \right )^{\dfrac {1}{2}} \cos \theta \label {7-32}\]
La gráfica polar de\(( Y^0_1)^2\) se muestra en la Figura\(\PageIndex{1}\). Para\(J = 1\) y\(m_J = 0\), la probabilidad de encontrar el eje internuclear es independiente del ángulo\(\varphi\) del eje x, y mayor para encontrar el eje internuclear a lo largo del eje z, pero también hay una probabilidad de encontrarlo en otros valores de\(\theta\) también. Entonces, aunque el eje internuclear no siempre está alineado con el eje z, la probabilidad es mayor para esta alineación. Además, dado que la probabilidad es independiente del ángulo\(\varphi\), el eje internuclear se puede encontrar en cualquier plano que contenga el eje z con igual probabilidad.
La\(m_J = 0\) función\(J = 1\), es 0 cuando\(\theta\) = 90°. Por lo tanto, todo el plano XY es un nodo. Este hecho significa que la probabilidad de encontrar el eje internuclear en este plano horizontal en particular es 0 en contradicción con nuestra imagen clásica de una molécula giratoria. En la imagen clásica, una molécula que gira en un plano perpendicular al plano xi debe tener el eje internuclear en el plano x dos veces en cada revolución, pero la descripción mecánica cuántica dice que la probabilidad de estar en el plano xi es cero. Esta conclusión significa que las moléculas no están rotando en el sentido clásico, pero aún tienen algunas, pero no todas, de las propiedades asociadas a la rotación clásica. Las propiedades que conservan están asociadas con el momento angular.
Ejercicio\(\PageIndex{9}\)
Para cada estado con\(J = 0\) y\(J = 1\), utilice la forma de función de los armónicos\(Y\) esféricos y la Figura\(\PageIndex{1}\) para determinar la orientación más probable del eje internuclear en una molécula diatómica, es decir, los valores más probables para\(\theta\) y\(\theta\).
Ejercicio\(\PageIndex{10}\)
Escribir un párrafo describiendo la información sobre una molécula giratoria que se proporciona en la gráfica polar de\(Pr [\theta, \theta ] \) para el\(J = 1\),\(m_J = \pm 1\) estado en la Figura\(\PageIndex{1}\). Compara esta información con la imagen clásica de un objeto giratorio.


