15.9: Problemas

Última actualización
Guardar como PDF

Page ID: 70103

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Problema\(\PageIndex{1}\)

Dado

\[\mathbf{A}=\begin{pmatrix} 2&3&-1 \\ -5&0&6\\ 0&2&3 \end{pmatrix}\; ;\mathbf{B}=\begin{pmatrix} 2 \\ 1\\0 \end{pmatrix}\; ;\mathbf{C}=\begin{pmatrix} 0&1\\ 2&0\\-1&3 \end{pmatrix} \nonumber\]

Multiplique todos los pares posibles de matrices.

Problema\(\PageIndex{2}\)

La representación matricial de un\(1/2\) sistema de espín fue introducida por Pauli en 1926. Las matrices de giro Pauli son la representación matricial del operador de momento angular para un\(1/2\) sistema de giro único y se definen como:

\[\mathbf{\sigma_x}=\begin{pmatrix} 0&1 \\ 1&0 \end{pmatrix}\; ;\mathbf{\sigma_y}=\begin{pmatrix} 0&-i \\ i&0 \end{pmatrix}\; ;\mathbf{\sigma_z}=\begin{pmatrix} 1&0\\ 0&-1 \end{pmatrix} \nonumber\]

Demostrar eso\(\mathbf{\sigma_x}\mathbf{\sigma_y}=i\mathbf{\sigma_z}\),\(\mathbf{\sigma_y}\mathbf{\sigma_z}=i\mathbf{\sigma_x}\) y\(\mathbf{\sigma_z}\mathbf{\sigma_x}=i\mathbf{\sigma_y}\)
Calcular el conmutador\(\left[\mathbf{\sigma_x},\mathbf{\sigma_y} \right]\).
Demostrar eso\(\mathbf{\sigma_x}^2=\mathbf{\sigma_y}^2=\mathbf{\sigma_z}^2=\mathbf{I}\), donde\(\mathbf{I}\) está la matriz de identidad. Pista: al igual que con los números, el cuadrado de una matriz es la matriz multiplicada por sí misma.

Problema\(\PageIndex{3}\)

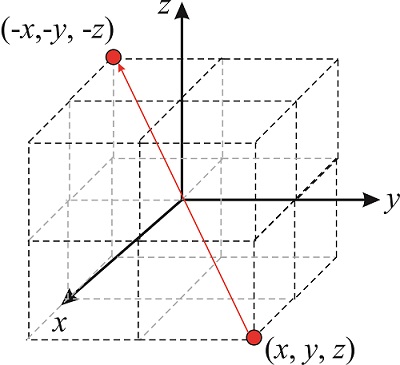
El operador de inversión,\(\hat i\) transforma el punto\((x,y,z)\) en\((-x,-y,-z)\). Anote la matriz que corresponda a este operador.

Figura\(\PageIndex{1}\): El operador de inversión (CC BY-NC-SA; Marcia Levitus)

Problema\(\PageIndex{4}\)

Calcular la inversa de\(\mathbf{A}\) por definición.

\[\mathbf{A}=\begin{pmatrix} 1&-2 \\ 0&1 \end{pmatrix} \nonumber\]

Problema\(\PageIndex{5}\)

Calcular la inversa de\(\mathbf{A}\) por definición.

\[\mathbf{A}=\begin{pmatrix} \cos \theta&-\sin \theta \\ \sin \theta&\cos \theta \end{pmatrix} \nonumber\]

Problema\(\PageIndex{6}\)

Encuentra los valores propios y los vectores propios nomalizados de

\[\mathbf{M_1}=\begin{pmatrix} 2&0 \\ 0&-3 \end{pmatrix} \nonumber\]

\[\mathbf{M_2}=\begin{pmatrix} 1&1+i \\ 1-i&1 \end{pmatrix} \nonumber\]

Problema\(\PageIndex{7}\)

Dado,

\[\mathbf{M_3}=\begin{pmatrix} 1&1-i \\ 1+i&1 \end{pmatrix} \nonumber\]

Demostrar que la matriz es hermitiana.
Calcular los vectores propios y demostrar que son ortogonales.