13.3: Anarmonicidad
- Page ID
- 74365
La energía electrónica de una molécula, ion o radical en geometrías cercanas a una estructura estable puede expandirse en una serie Taylor en potencias de coordenadas de desplazamiento como se hizo en la sección anterior de este Capítulo. Esta expansión conduce a una imagen de los niveles de energía vibratoria armónica desacoplada
\[ E(v_1 ... V_{3N - 5 \text{ or }6}) = \sum\limits_{j=1}^{3N-5 \text{ or }6}\hbar\omega _j\left( v_j + \frac{1}{2} \right) \]
y funciones de onda
\[ \Psi(x_1 ... x_{3N-5\text{ or }6} = ^{3N-5 \text{ or }}_{j=1} \Psi_{vj}(x_j). \]
El espaciamiento entre los niveles de energía en el que uno de los números cuánticos de modo normal aumenta por unidad
\[ \Delta E_{vj} = E(... v_j + 1 ... ) - E(...v_j ... ) = \hbar\omega_j \]
se predice que sea independiente del número cuántico vj. Esta imagen de niveles de energía uniformemente espaciados
\[ \Delta E_0 = \Delta E_1 = \Delta E_2 = ... \]
es un aspecto incorrecto del modelo armónico del movimiento vibratorio, y es el resultado del modelo cuadrático para la superficie de energía potencial\(V(x_j).\)
La expansión de E (v) en Poderes de\(\left(v+\dfrac{1}{2}\right).\)
La evidencia experimental indica claramente que las desviaciones significativas de la expresión de energía del oscilador armónico ocurren a medida que\(v_j\) crece el número cuántico. En el Capítulo 1 estas desviaciones se explicaron en términos del verdadero potencial V (R) de la molécula diatómica que se desvía fuertemente del\( \frac{1}{2k}(E-E_e)^2 \) potencial armónico a mayor energía (y por lo tanto mayor\(|R-R_e|)\) como se muestra en la siguiente figura.
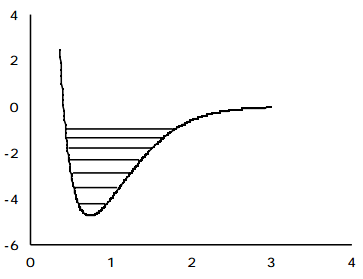
A longitudes de enlace más grandes, el verdadero potencial es “más suave” que el potencial armónico, y finalmente alcanza su asíntota que se encuentra en la energía de disociación\(D_e\) por encima de su mínimo. Esta desviación negativa de la verdadera V (R)\( \frac{1}{2k}(R-R_e)^2\) hace que los verdaderos niveles de energía vibracional se encuentren por debajo de las predicciones armónicas.
Es convencional expresar los niveles de energía vibratoria observados experimentalmente, a lo largo de cada uno de los modos 3N-5 o 6 independientes, de la siguiente manera:
\[ E(v_j) = \hbar\left[ \omega_j\left(v_j + \frac{1}{2}\right) - (\omega x)_j \left(v_j + \frac{1}{2}\right)^2 + (\omega y)_j \left(v_j + \frac{1}{2}\right)^3 + (\omega z)_j \left( v_j + \frac{1}{2} \right)^4 + ... \right] \]
El primer término es la expresión armónica. El siguiente se denomina la primera anarmonicidad; (generalmente) produce una contribución negativa a E\((v_j)\) que varía como\( \left( v_j + \frac{1}{2} \right)^2 \). El espaciamiento entre los niveles de\(v_j \rightarrow v_j + 1 \) energía sucesivos viene dado entonces por:
\[ \Delta E_{vj} = E()v_j + 1) - E(v_j) \]
\[ = \hbar [\omega_j - 2(\omega x)_j (v_j + 1) + ...]\]
Una gráfica del espaciamiento entre los niveles de energía vecinos versus\(v_j\) debe ser lineal para valores de vj donde dominan los términos armónico y primer armónico. Se espera que la pendiente de dicha parcela sea\(-2\hbar(\omega x)_j\) y la pequeña\(-v_j\) intercepción debe ser\(\hbar[\omega_j - 2(\omega x)_j ].\) Tal gráfica de datos experimentales, que claramente se puede utilizar para determinar el\(\omega_j \text{ and } (\omega x)_j\) parámetro del modo de estudio vibracional, se muestra en la figura a continuación.
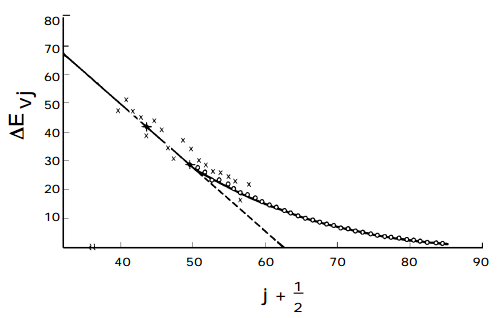
La Extrapolación de los Esponjares
Estas llamadas gráficas Birge-Sponer también se pueden utilizar para determinar las energías de disociación de las moléculas. Al extrapolar linealmente la gráfica de\(\Delta E_{vj}\) valores experimentales a valores vj grandes, se puede encontrar el valor\(v_j\) en el que el espaciamiento entre los niveles vibracionales vecinos va a cero. Este valor\(v_j\), max especifica el número cuántico del último nivel vibratorio límite para la función energética potencial particular\(V(x_j)\) de interés. La energía de disociación se\(D_e\) puede calcular añadiendo a\( \frac{1}{2}\hbar\omega _j \) (la energía del punto cero a lo largo de este modo) la suma de las distancias entre los niveles de energía vibratoria vecinos de\(v_j = 0 \text{ to } v_j = v_j,\text{ max }\):
\[ D_e \frac{1}{2}\hbar \omega_j + ^{v_j \text{ max }}_{v_j \text{ = 0 }}\Delta E_{v_j}. \]
Dado que los datos experimentales no suelen estar disponibles para todo el rango de\(v_j\) valores (de 0 a\(v_j\), max), esta suma debe calcularse usando la expresión anarmónica para\(\Delta E_{v_j}\):
\[ \Delta E_{v_j} = \hbar \left[ \omega_j - 2(\omega x)_j \left( v_j + \dfrac{1}{2} + ... \right) \right]. \]
Alternativamente, la suma se puede calcular a partir de la gráfica Birge-Sponer midiendo el área bajo el ajuste de línea recta a la gráfica de\(\Delta E_{v_j} \text{ or } v_j \text{ from } v_j = 0 \text{ to } v_j = v_{j,\text{ max }}.\)
Esto completa nuestra introducción al tema de los movimientos rotacionales y vibracionales de las moléculas (que se aplica igualmente bien a iones y radicales). La información contenida en esta Sección se utiliza nuevamente en la Sección 5 donde se examinan las transiciones inducidas por fotones entre pares de estados propios moleculares electrónicos, vibracionales y rotacionales. Los tratamientos más avanzados de la materia de esta Sección se encuentran en el texto de Wilson, Decius y Cross, así como en el texto de Zare sobre el momento angular.
Colaboradores y Atribuciones
Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry and Jeff A. Nichols (Oak Ridge National Laboratory)


