15.1: Transiciones rotacionales
- Page ID
- 74422
Dentro de la aproximación de que los estados electrónicos, vibracionales y rotacionales de una molécula pueden tratarse como independientes, la función de onda molecular total del estado “inicial” es un producto
\[ \Phi_i = \psi_{ei} \chi_{vi} \phi_{ri} \]
de una función electrónica\(\psi_{ei}, \text{ a vibrational function } \chi_{vi}, \text{ and a rotational function } \phi_{ri}. \text{ A similar product expression holds for the "final" wavefunction } \Phi_f.\)
En la espectroscopia de microondas, la energía de la radiación se encuentra en el rango de fracciones de a\(cm^{-1} \text{ through several } cm^{-1}\); tales energías son adecuadas para excitar movimientos rotacionales de moléculas pero no son lo suficientemente altas como para excitar cualquier vibración excepto las más débiles (por ejemplo, las de los complejos de Van der Waals débilmente unidos). En las transiciones rotacionales, los estados electrónico y vibratorio quedan así inalterados por el proceso de excitación; de ahí\(\psi_{ei} = \psi_{ef} \text{ and } \chi_{vi} = \chi_{vf}.\)
Aplicación de expresiones de velocidad de transición dipolo eléctrico de primer orden
\[ R_{i,f} = 2\pi g(\omega_{f,i}) |\alpha_{f,i}|^2 \]
obtenido en el Capítulo 14 a este caso requiere que la aproximación E1
\[ R_{i,f} = \left( \dfrac{2\pi}{\hbar^2} \right) g(\omega_{f,i}) | \textbf{E}_0\cdot{\langle}\Phi_f |\mu | \Phi_i \rangle |^2 \]
ser examinados con más detalle. Específicamente, los elementos de matriz dipolo eléctrico\( \langle \Phi_f | \mu | \Phi_i \rangle \text{ with } \mu = \sum\limits_j e \textbf{r}_j + \sum\limits_a Z_a e \textbf{R}_a \) deben ser analizados por\(\Phi_i \text{ and } \Phi_f\) ser de la forma del producto que se muestra anteriormente.
Las integraciones sobre las coordenadas electrónicas contenidas en, así\( \langle \Phi_f |\mu |\Phi_i \rangle ,\) como las integraciones sobre grados de libertad vibracionales, producen “valores de expectativa” del operador de momento dipolo eléctrico porque los componentes electrónicos y vibracionales de\( \Phi_i \text{ and } \Phi_f\) son idénticos:
\[ \langle \psi_{ei}| \mu | \psi_{ei} \rangle = \mu(\textbf{R}) \]
es el momento dipolar del estado electrónico inicial (que es una función de los grados geométricos internos de libertad de la molécula, denotado R); y
\[ \langle \chi_{vi} | \mu (\textbf{R} ) |\chi_{vi} \rangle = \mu_{ave} \]
es el momento dipolar promediado vibracionalmente para el estado vibracional particular etiquetado\(\chi_{vi}. \text{ The vector } \mu_{ave}\) mave tiene componentes a lo largo de varias direcciones y puede verse como un vector “bloqueado” al eje de coordenadas internas de la molécula (etiquetado a, b, c como se indica a continuación).
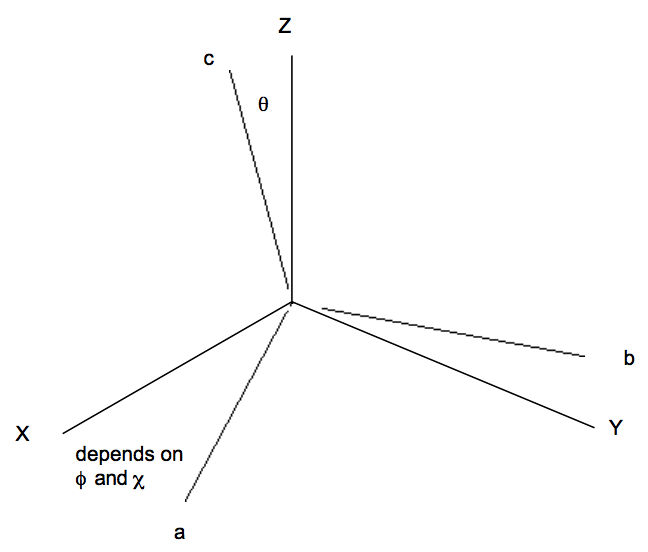
La parte rotacional de la\( \langle \Phi_f | \mu | \Phi_i \rangle \) integral no es de la forma del valor de expectativa debido a la función rotacional inicial\(\phi_{ir} \text{ is not the same as the final } \phi_{fr}\). Esta integral tiene la forma:
\[ \langle \Phi_{ir} | \mu_{ave} | \Phi_{fr} \rangle = \int (Y^{\text{*}}_{L,M}(\theta,\phi)) \mu_{ave} Y_{\text{L', M'}}(\theta, \phi) \text{ sin}\theta \text{ d}\theta \text{ d}\phi \]
o moléculas lineales cuyas funciones de onda rotacionales iniciales y finales son\(Y_{\text{L,M}} \text{ and } Y_{\text{L',M'}} \), respectivamente, y
\[ \langle \phi_{ir} | \mu_{ave} | \phi_{fr} \rangle = \sqrt{\dfrac{2L + 1}{8\pi^2}}\sqrt{\dfrac{2L' + 1}{8\pi^2}} \]
\[ \int \left( D_{\text{L, M, K}}(\theta , \phi , \chi) \mu_{ave} D^{\text{*}}_{\text{L', M', K'}}(\theta , \phi , \chi) \text{ sin}\theta \text{ d}\theta \text{ d}\phi \text{ d}\chi \right) \]
para moléculas superiores esféricas o simétricas (aquí,\( \sqrt{\dfrac{2L + 1}{8\pi^2}}D^{\text{*}}_{\text{L, M, K}}(\theta , \phi , \chi) \) están las funciones de onda rotacionales normalizadas descritas en el Capítulo 13 y en el Apéndice G). Los ángulos\(\theta , \phi , \text{ and } \chi\) se refieren a cómo se orienta el sistema de coordenadas de moléculas fijas con respecto al sistema de ejes X, Y, Z fijos en el espacio.
Moléculas Lineales
Para las moléculas lineales, el momento dipolar promediado vibracionalmente\(\mu_{ave}\) se encuentra a lo largo del eje molecular; de ahí su orientación en el sistema de coordenadas fijadas en laboratorio puede especificarse en términos de los mismos ángulos\((\theta \text{ and } \phi)\) que se utilizan para describir las funciones rotacionales.\(Y_{\text{L,M}} (\theta ,\phi ).\) Por lo tanto, los tres componentes de la\( \langle \phi_{ir} | \mu_{ave} | \phi_{fr} \rangle\) integral se puede escribir como:
\[ \langle \phi_{ir} | \mu_{ave} | \phi_{fr} \rangle_x = \mu \int Y^{\text{*}}_{\text{L, M}}(\theta ,\phi) \text{ sin}\theta \text{ cos}\phi \text{ Y}_{\text{L', M'}}(\theta , \phi )\text{ sin}\theta \text{ d}\theta \text{ d}\phi \]
\[ \langle \phi_{ir} | \mu_{ave} | \phi_{fr} \rangle_y = \mu \int Y^{\text{*}}_{\text{L, M}}(\theta ,\phi) \text{ sin}\theta \text{ cos}\phi \text{ Y}_{\text{L', M'}}(\theta , \phi )\text{ sin}\theta \text{ d}\theta \text{ d}\phi \]
\[ \langle \phi_{ir} | \mu_{ave} | \phi_{fr} \rangle_z = \mu \int Y^{\text{*}}_{\text{L, M}}(\theta ,\phi) \text{ sin}\theta \text{ cos}\phi \text{ Y}_{\text{L', M'}}(\theta , \phi )\text{ sin}\theta \text{ d}\theta \text{ d}\phi \]
donde\(\mu\) está la magnitud del momento dipolo promediado. Si la molécula no tiene momento dipolar, todas las integrales dipolares eléctricas anteriores desaparecen y la intensidad de las transiciones rotacionales E1 es cero.
Las tres integrales E1 pueden analizarse más a fondo señalando que cos\( \theta \propto \text{ Y}_{\text{1,0}}; \text{ sin}\theta \text{ cos}\phi \propto \text{ Y}_{\text{1,1}} + \text{ Y}_{\text{1,-1}}; \text{ and sin}\theta \text{ sin}\phi \propto \text{ Y}_{\text{1,1}} - \text{ Y}_{\text{1,-1}}\) y utilizando los métodos de acoplamiento de momento angular ilustrados en el Apéndice G. En particular, el resultado dado en ese apéndice:
\[ D_{\text{j, m, m'}}D_{\text{l, n, n'}} = \sum\limits_{\text{J, M, M'}}\langle J,M|j,m; l,n\rangle \langle j,m'; l,n'|J,M' \rangle D_{\text{J, M, M'}} \]
cuando se multiplica por D\(^{\text{*}}_{\text{J, M, M'}} \text{ and integrated over sin}\theta \text{ d}\theta \text{ d}\phi \text{ d}\chi\), rinde:
\[ \int D^{\text{*}}_{\text{J, M, M'}} D_{\text{j, m, m'}}D_{\text{l, n, n'}} \text{ sin}\theta\text{ d}\theta \text{ d}\phi \text{ d}\chi \]
\[ = \dfrac{8\pi^2}{2J+1}\langle \text{ J,M| j,m ; l,n }\rangle \langle \text{ j,m' ; l,n'|J, M' } \rangle \]
\[ = 8\pi^2 \left( \dfrac{jlJ}{mn-M} \right) \left( \dfrac{jlJ}{m'n'-M'} \right) \left( -1 \right)^{\text{M+M'}}. \]
Para utilizar este resultado en el presente caso de molécula lineal, observamos que las\(D_{\text{J,M,K}} \text{ functions and the Y}_{\text{J,M}}\) funciones están relacionadas por:
\[ \text{Y}_{\text{J,M}}(\theta ,\phi ) = \sqrt{\dfrac{2J + 1}{4\pi}} D^{\text{*}}_{\text{J, M, 0}}(\theta ,\phi ,\chi). \]
El factor de normalización se\( \sqrt{\frac{2J + 1}{4\pi}} \text{ rather than} \sqrt{\frac{2J + 1}{8\pi^2}}\) debe ahora a que ya no\(\text{Y}_{\text{J,M}}\) son funciones de\(\chi\), y así\( 0 \leq \chi \leq 1\pi\) desaparece la necesidad de integrarse sobre. De igual manera, el\(\chi \text{-dependence of}\)\(\text{D}^{\text{*}}_{\text{J,M,K}}\) desaparece para K = 0.
Ahora usamos estas identidades en las tres integrales E1 de la forma
\[ \mu \int Y^{\text{*}}_{\text{L,M}}(\theta ,\phi) Y_{\text{1,m}}(\theta , \phi) Y_{\text{L',M'}}(\theta ,\phi)\text{ sin}\theta \text{ d}\theta \text{ d}\phi , \]
siendo m = 0 la integral del eje Z, y las integrales de los ejes Y y X son combinaciones de los resultados m = 1 y m = -1. Hacerlo rinde:
\[ \mu \int Y^{\text{*}}_{\text{L,M}}(\theta , \phi) Y_{\text{1,m}}(\theta ,\phi )\text{ Y}_{\text{L', M'}}(\theta ,\phi) \text{ sin}\theta \theta{ d}\theta \text{ d}\phi \]
\[ =\mu \sqrt{\dfrac{2L + 1}{4\pi} \dfrac{2L' + 1}{4\pi} \dfrac{3}{4\pi}}\int D_{\text{L, M, 0}}\textbf{ D}^{\text{*}}_{\text{l, m, 0}}\textbf{D}^{\text{*}}_{\text{L', M', 0}} \text{ sin}\theta \text{ d}\theta \text{ d}\phi \text{ d}\dfrac{\chi}{2\pi}. \]
El último factor de\(1/2\pi\) se inserta para cancelar la integración sobre\(d\chi \) eso, porque todos los factores K en las matrices de rotación son iguales a cero, rinden trivialmente\(2\pi \). Ahora, usando el resultado mostrado anteriormente expresando la integral sobre tres matrices de rotación, estas integrales E1 para el caso de linearmolecule reducen a:
\[ \mu \int\text{ Y}^{\text{*}}_{\text{L,M}}(\theta , \phi)\text{ Y}_{\text{1,m}}(\theta ,\phi)\text{ Y}_{\text{L',M'}}(\theta ,\phi)\text{ sin}\theta \text{ d}\theta \text{ d}\phi \]
\[ = \mu \sqrt{\dfrac{2L + 1}{4\pi}\dfrac{2L' + 1}{4\pi}\dfrac{3}{4\pi}}\dfrac{8\pi^2}{2\pi}\left( \dfrac{L' 1 L}{M'm-M} \right)\left( \dfrac{L' 1 L}{0 0 -0} \right)(-1)^M \]
\[ \mu\sqrt{(2L + 1)(2L' + 1)\dfrac{3}{4\pi}}\left( \dfrac{L' 1 L}{M' m -M} \right) \left( \dfrac{L' 1 L}{0 0 -0} \right) (-1)^M. \]
Aplicado a la integral del eje z (identificando m = 0), este resultado desaparece a menos que:
\[ \text{M} = \text{M'} \]
y
\[ \text{L} = \text{L'} + 1 \text{ or L' }- 1. \]
Aunque las consideraciones de acoplamiento de momento angular permitirían L = L' (porque acoplar dos momentos angulares con j = 1 y j = L' debería dar L'+1, L' y L'-1), el símbolo 3-j\( \left( \dfrac{\text{L' 1 L}}{\text{0 0 -0}} \right) \) desaparece para el caso L = L' ya que los símbolos 3-j tienen la siguiente simetría
\[ \left( \dfrac{\text{L' 1 L}}{\text{M' m -M}} \right) = (-1)^{\text{L+L'+1}} \left( \dfrac{\text{L' 1 L}}{\text{-M' -m M}} \right) \]
con respecto a los índices M, M' y m. Aplicado al símbolo\( \left( \dfrac{\text{L' 1 L}}{\text{0 0 -0}} \right) \) 3-j, esto significa que este elemento 3-j particular desaparece para L = L' ya que L + L' + 1 es impar y por lo tanto\((-1)^{\text{L + L' + 1}}\) es -1.
Aplicado a las integrales de los ejes x e y, que contienen componentes m = ± 1, este mismo análisis produce:
\[ \mu \sqrt{\text{(2L + 1)(2L' + 1)}\dfrac{3}{4\pi}}\left( \dfrac{\text{L' 1 L}}{M' \pm 1 -M} \right) \left( \dfrac{\text{L' 1 L}}{\text{0 0 -0}} \right) (-1)^M \]
que luego requiere que
\[ \text{M} = \text{M'} \pm 1 \]
y
\[ \text{L} = \text{ L' + 1, L' -1} \]
con L = L' nuevamente prohibido por el segundo símbolo 3-j.
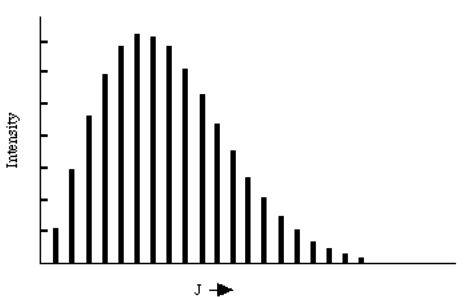
Estos resultados proporcionan las llamadas "reglas de selección" porque el límite de los valores L y M del estado rotacional final, dados los valores L', M' del estado rotacional inicial. En la figura que se muestra a continuación, se da el espectro de absorción L = L' + 1 de NO a 120 °K. Las intensidades de los diversos picos están relacionadas con las poblaciones de los estados rotacionales de menor energía que son, a su vez, proporcionales a\((2 L' + 1) e^{(- L'(L'+1) \dfrac{\hbar^2}{8\pi^2IkT}}.\) También se incluyen en las intensidades los llamados factores de fuerza de línea que son proporcionales a los cuadrados de las cantidades:
\[ \mu \sqrt{ (2L + 1)(2L' + 1)\dfrac{3}{4\pi} }\left( \dfrac{\text{L' 1 L}}{M' m -M} \right) \left( \dfrac{\text{L' 1 L}}{\text{0 0 -0}} \right)(-1)^M \]
que aparecen en las integrales E1 analizadas anteriormente (recordemos que la tasa de absorción de fotones\( R_{i,f} = \left( \frac{2\pi}{\hbar^2} \right)g(\omega_{f,i}) | \textbf{E}_0\cdot{\langle}\Phi_f | \mu | \Phi_i \rangle |^2 \) involucra los cuadrados de estos elementos de la matriz). El libro de Zare brinda un excelente tratamiento de las contribuciones de los factores de fuerza de línea a la rotación, vibración e intensidades de línea electrónicas.
Moléculas no lineales
Para las moléculas que son no lineales y cuyas funciones de onda rotacionales se dan en términos de las funciones superiores esféricas o simétricas\(\textbf{D}^{\text{*}}_{\text{L,M,K}}\), el momento dipolar\(\mu_{ave}\) puede tener componentes a lo largo de cualquiera o las tres coordenadas internas de la molécula (por ejemplo, las tres coordenadas fijas de moléculas que describen la orientación de los ejes principales del tensor momento de inercia). Para una molécula superior esférica, se\(| \mu_{ave} |\) desvanece, por lo que las transiciones E1 no ocurren.
Para las especies superiores simétricas,\(\mu_{ave}\) se encuentra a lo largo del eje de simetría de la molécula, por lo que la orientación de\(\mu_{ave}\) puede describirse nuevamente en términos de\(\theta \text{ and } \phi \), los ángulos utilizados para ubicar la orientación del eje de simetría de la molécula en relación con el sistema de coordenadas fijado en laboratorio. Como resultado, la integral E1 nuevamente se puede descomponer en tres piezas:
\[ \langle \phi_{ir} | \mu_{ave} | \phi_{fr}\rangle_x = \mu\int D_{\text{L, M, K}}(\theta ,\phi ,\chi)\text{ cos}\theta \text{ cos}\phi D^{\text{*}}_{\text{L', M', K'}}(\theta , \phi , \chi)\text{ sin}\theta \text{ d}\theta \text{ d}\phi \text{ d}\chi \]
\[ \langle \phi_{ir} | \mu_{ave} | \phi_{fr}\rangle_y = \mu\int D_{\text{L, M, K}}(\theta ,\phi ,\chi)\text{ cos}\theta \text{ sin}\phi D^{\text{*}}_{\text{L', M', K'}}(\theta , \phi , \chi)\text{ sin}\theta \text{ d}\theta \text{ d}\phi \text{ d}\chi \]
\[ \langle \phi_{ir} | \mu_{ave} | \phi_{fr}\rangle_z = \mu\int D_{\text{L, M, K}}(\theta ,\phi ,\chi) \text{ cos}\theta D^{\text{*}}_{\text{L', M', K'}}(\theta , \phi , \chi)\text{ sin}\theta \text{ d}\theta \text{ d}\phi \text{ d}\chi \]
Utilizando el hecho de que\( \text{ cos}\theta \propto \text{D}^{\text{*}}_{\text{1, 0,0}}; \text{ sin}\theta \text{ cos}\phi \propto \text{D}^{\text{*}}_{\text{1,1,0}} + \text{D}^{\text{*}}_{\text{1,-1,0}}; \text{ and sin}\theta \text{ sin}\phi \propto \text{D}^{\text{*}}_{\text{1,1,0}} - \text{D}^{\text{*}}_{\text{1,-1,0}}\) y las herramientas de acoplamiento de momento angular permite que estas integrales se expresen, como anteriormente, en términos de productos de los siguientes símbolos 3-j:
\[ \left( \dfrac{\text{L' 1 L}}{\text{M' m -M}} \right) \left( \dfrac{\text{L' 1 L}}{\text{K' 0 -K}} \right), \]
de la que se derivan las siguientes reglas de selección:
\[ \text{L} = \text{L' + 1, L', L' - 1} \text{ (but not L = L' = 0)} \]
\[ \text{K = K'} \]
\[ \text{M = M' + m,} \]
con m = 0 para la integral del eje Z y m = ± 1 para las integrales de los ejes X e Y. Además, si K = K' = 0, las transiciones L = L' también están prohibidas por la desaparición del segundo símbolo 3-j.
Colaboradores y Atribuciones
Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry and Jeff A. Nichols (Oak Ridge National Laboratory)


