15.4: Expresiones de función de correlación de tiempo para tasas de transición

La expresión E1 de “regla de oro” de primer orden para las tasas de transiciones inducidas por fotones se puede refundir en una forma en la que ciertos modelos físicos específicos se introducen fácilmente y se obtienen conocimientos fácilmente. Además, mediante el uso de las llamadas funciones de correlación de tiempo promediado en equilibrio, es posible obtener expresiones de velocidad apropiadas para un gran número de moléculas que existen en una distribución de estados iniciales (por ejemplo, para moléculas que ocupan muchos posibles niveles rotacionales y quizás varios niveles vibracionales en la habitación temperatura).

Tasa de absorción o emisión de energía de estado a estado

Para comenzar, la expresión obtenida anteriormente

\[ R_{i,f} = \left( \dfrac{2\pi}{\hbar^2}\right) g(\omega_{f,i}) | \textbf{E}_0 \cdot{\langle} \phi_f | \mu | \Phi_i \rangle |^2, \]

que es apropiado para las transiciones entre un estado inicial particular\(\Phi_i \) y un estado final específico\(\Phi_f\), se reescribe como

\[ R_{i,f} = \left( \dfrac{2\pi}{\hbar^2}\right) \int g( \omega ) | \textbf{E}_0 \cdot{\langle} \phi_i | \mu | \phi_i \rangle |^2 \delta (\omega_{f,i} - \omega )\text{ d}\omega . \]

Aquí, la\(\delta (\omega_{f,i} - \omega )\) función se utiliza para imponer específicamente la “condición de resonancia” que resultó en el tratamiento de perturbación dependiente del tiempo dado en el Capítulo 14; establece que la frecuencia de los fotones\(\omega\) debe ser resonante con la frecuencia de transición\(\omega_{f,i}\). Cabe señalar que\(\omega\) al permitir atropellar valores positivos y negativos, la absorción de fotones (con\(\omega_{f,i}\) positivo y por lo tanto w positivo) y el caso de emisión estimulada (con\(\omega_{f,i}\) negativo y por lo tanto\(\omega\) negativo) se incluyen en esta expresión (siempre que g ( \(\omega\)) se define como g (|\(\omega\) |) de manera que las\(\omega\) contribuciones negativas se multiplican por la intensidad de la fuente de luz al\(\omega\) valor positivo correspondiente).

La siguiente identidad integral se puede utilizar para reemplazar la\(\delta\) función -function:

\[ \delta (\omega_{f,i} - \omega ) = \dfrac{1}{2\pi} \int\limits_{-\infty}^{\infty} e^{i(\omega_{f,i} - \omega )t} \text{ dt} \]

por una forma que es más susceptible de un mayor desarrollo. Entonces, la tasa de transición de estado a estado se convierte en:

\[ R_{i,f} = \left(\dfrac{1}{\hbar}\right) \int g(\omega ) | \textbf{E}_0 \cdot{\langle}\phi_f | \mu | \phi_i \rangle |^2 \int\limits_{-\infty}^{\infty}e^{i(\omega_{f,i} - \omega)t} \text{ dt d}\omega . \]

Promediando sobre el equilibrio de la población Boltzmann de los Estados iniciales

Si esta expresión se multiplica entonces por la probabilidad de equilibrio de\(\rho_i\) que la molécula se encuentre en el estado\(\Phi_i\) y se sume sobre todos esos estados iniciales y se sume sobre todos los estados finales a los\(\Phi_f\) que se pueda alcanzar\(\Phi_i\) con fotones de energía\(\hbar \omega\), la se obtiene la tasa promedio de equilibrio de absorción de fotones por la muestra molecular:

\[ R_{\text{eq.ave.}} = \left( \dfrac{1}{\hbar^2} \right) \sum\limits_{i,f} \rho_i \]

\[ \int g(\omega ) | \textbf{E}_0 \cdot{\langle}\Phi_f | \mu | \Phi_i \rangle |^2 \int\limits_{-\infty}^{\infty} e^{i(\omega_{f,i} - \omega )t} \text{dt d}\omega . \]

Esta expresión es apropiada para un conjunto de moléculas que pueden estar en diversos estados iniciales\(\Phi_i\) con probabilidades\(\rho_i\). El resultado correspondiente para las transiciones que se originan en un estado particular (\(\Phi_i\)) pero terminan en cualquiera de los estados finales “permitidos” (por reglas de energía y selección) dice:

\[ R_{\text{state i.}} = \left( \dfrac{1}{\hbar^2} \right) \sum\limits_f \int g(\omega ) | \textbf{E}_0 \cdot{\langle}\Phi_f | \mu | \Phi_i \rangle |^2 \]

\[ \int\limits_{-\infty}^{\infty} e^{i(\omega_{f,i} - \omega )t}\text{ dtd}\omega . \]

Para un conjunto canónico, en el que se especifica el número de moléculas, la temperatura y el volumen del sistema,\(\rho_i\) toma la forma:

\[ \phi_i = \dfrac{g_i}{Q}e^{-\dfrac{E_i^0}{kT}} \]

donde Q es la función de partición canónica de las moléculas y\(g_i\) es la degeneración del estado\(\Phi_i\) cuya energía es\(\text{E}_i^0.\)

En la expresión anterior for\(\text{R}_{\text{eq.ave.}}\), se produce una doble suma. Escribiendo en detalle los elementos que aparecen en esta suma, se encuentra:

\[ \sum\limits_{i,f} \phi_i \textbf{E}_0 \cdot{\langle} \Phi_i | \mu | \Phi_f \rangle \textbf{E}_0 \cdot{\langle}\Phi_f | \mu | \Phi_i \rangle e^{i(\omega_{f,i})t}. \]

En situaciones en las que uno está interesado en desarrollar una expresión de la intensidad que surge de las transiciones a todos los estados finales permitidos, la suma sobre estos estados finales puede llevarse a cabo explícitamente por escrito primero

\[ \langle \Phi_f | \mu | \Phi_i \rangle e^{i(\omega_{f,i})t} = \langle \Phi_f | e^{\dfrac{iHt}{\hbar}} \mu e^{-\dfrac{iHt}{\hbar}} | \Phi_i \rangle \]

y luego usando el hecho de que el conjunto de estados {\(\Phi_k\)} son completos y por lo tanto obedecen

\[ \sum\limits_k | \Phi_k \rangle \langle \Phi_k | = 1.\]

El resultado de usar estas identidades así como la definición de Heisenberg de la dependencia del tiempo del operador dipolo

\[ \mu (t) = e^{\dfrac{iHt}{\hbar}} \mu e^{-\dfrac{iHt}{\hbar}}, \]

es:

\[ \sum\limits_i \rho_i \langle \Phi | \textbf{E}_0 \cdot{\mu} \textbf{E}_0\cdot{\mu}(t) | \Phi_i \rangle . \]

De esta forma, se dice que la dependencia del tiempo se ha reducido a la de una función de correlación de tiempo promediada en equilibrio (n.b., la\( \sum\limits_i \rho_i \langle \Phi_i | | \Phi_i \rangle \)) que involucra al componente del operador dipolo a lo largo del campo eléctrico externo a t = 0 (\(\textbf{E}_0\cdot{\mu}\)) y este componente en un momento diferente \( t(\textbf{E}_0\cdot{\mu}(t))\).

Emisión y Absorción de Fotones

Si\(\omega_{f,i}\) es positivo (es decir, en el caso de absorción de fotones), la expresión anterior producirá una contribución distinta de cero cuando se multiplique por\(e^{-i \omega t}\) e integrada sobre\(\omega \) valores positivos. Si\(\omega_{f,i}\) es negativo (en cuanto a la emisión estimulada de fotones), esta expresión contribuirá, nuevamente cuando se multiplique por\(e^{-i\omega t}\), para\(\omega \) valores negativos. En esta última situación,\(\rho_i\) se encuentra la probabilidad de equilibrio de encontrar la molécula en el estado (excitado) a partir del cual se producirá la emisión; esta probabilidad puede estar relacionada con la del estado inferior\(\rho_f\) por

\[ \rho_{\text{excited}} = \rho_{\text{lower}} e^{-\dfrac{(\text{E}^0_{\text{excited}} - \text{E}^0_{\text{lower}})}{kT}} \]

\[ = \rho_{\text{lower}}e^{-\dfrac{\hbar \omega}{kT}}. \]

De esta forma, es importante darse cuenta de que los estados excitados e inferiores son tratados como estados individuales, no como niveles que podrían contener un conjunto degenerado de estados.

Los casos de absorción y emisión se pueden combinar en una sola expresión neta para la tasa de absorción de fotones reconociendo que este último proceso conduce a la producción de fotones, y por lo tanto debe ingresarse con un signo negativo. La expresión resultante para la tasa neta de disminución de fotones es:

\[ \text{R}_{\text{eq.ave.net}} = \left( \dfrac{1}{\hbar^2} \right) \sum\limits_i \rho_i \left( 1 - e^{-\dfrac{\hbar \omega}{kT}} \right) \]

\[ \iint g(\omega ) \langle \Phi_i | (\textbf{E}_0 \cdot{\mu} ) \textbf{E}_0 \cdot{\mu}(t) | \Phi_i \rangle e^{-i\omega t} \,d\omega \,dt. \]

Las funciones de forma de línea y correlación de tiempo

Ahora bien, es convención introducir la llamada función de “forma de línea”\(I(\omega)\):

\[ I(\omega ) = \sum\limits_i \rho_i \int \langle \Phi_i | (\textbf{E}_0 \cdot{\mu}) \textbf{E}_0\cdot{\mu} (t) | \Phi_i \rangle e^{-i\omega t}\, dt \]

en términos de los cuales la tasa neta de absorción de fotones es

\[ \text{R}_{\text{eq.ave.net}} = \left( \dfrac{1}{\hbar^2} \right) \left( 1 -e^{-\hbar \omega/kT}\right) \int g(\omega )I(\omega ) \text{ d}\omega . \]

Como se indicó anteriormente, la función

\[ \text{C}(t) = \sum\limits_i \rho_i \langle \Phi_i | \textbf{E}_0 \cdot{\mu} ) \textbf{E}_0\cdot{\mu}(t) | \Phi_i \rangle \]

se denomina función de correlación de tiempo promedio de equilibrio del componente del operador dipolo eléctrico a lo largo de la dirección del campo eléctrico externo\(\textbf{E}_0\). Su transformada de Fourier es\(I(\omega)\), la función de forma de línea espectral. La convolución de\(I(\omega)\) con la función de la fuente de luz (\ g (\ omega\)), multiplicada por\(\left(1 - e^{-\frac{h \omega}{kT}} \right)\), la corrección para la emisión estimulada de fotones, da la tasa neta de absorción de fotones.

Contribuciones rotacionales, traslacionales y vibracionales a la función de correlación

Para aplicar la maquinaria de función de correlación de tiempo a cada tipo particular de transición espectroscópica, se procede de la siguiente manera:

Transiciones rotacionales puros

Para las transiciones puramente rotacionales, los estados electrónicos y vibracionales inicial y final son los mismos. Por otra parte, los estados electrónico y vibracional no se suman en el análogo del desarrollo anterior porque uno está interesado en obtener una expresión para el lineshape de una transición\( \chi_{\text{iv}} \psi_{\text{ie}} \rightarrow \chi_{\text{fv}} \psi_{\text{fe}} \) electrónica-vibracional particular. Como resultado, la suma sobre estados finales contenida en la expresión (ver anteriormente)

\[ \sum\limits_{\text{i,f}} \rho_i \textbf{E}_0 \cdot{\langle} \Phi_{\text{i}} | \mu | \Phi_{\text{f}} \rangle \textbf{E}_0 \cdot{\langle} \Phi_{\text{f}} | \mu (t) | \Phi_{\text{i}} \rangle e^{i(\omega_{\text{f,i}})t} \]

se aplica únicamente a la suma sobre los estados rotacionales finales. Con más detalle, esto se puede mostrar de la siguiente manera:

\[ \sum\limits_{\text{i,f}} \rho_{\text{i}} \textbf{E}_0 \cdot{\langle}\Phi_{\text{i}} | \mu | \Phi_{\text{f}} \rangle \textbf{E}_0 \cdot{\rangle} \Phi_{\text{f}} | \mu (t) | \Phi_{\text{i}} \rangle \]

\[ =\sum\limits_{\text{i,f}} \rho_{\text{i}} \textbf{E}_0 \cdot{\langle} \phi_{\text{ir}} \chi_{\text{iv}} \psi_{\text{ie}} | \mu | \phi_{\text{fr}} \chi_{\text{iv}} \psi_{\text{ie}} \rangle \textbf{E}_0 \cdot{\langle} \phi_{\text{fr}} \chi_{\text{iv}} \psi_{\text{ie}} | \mu (t) | \phi_{\text{ir}} \chi_{\text{iv}} \psi_{\text{ie}} \rangle \]

\[ =\sum\limits_{\text{i,f}} \rho_{\text{ir}} \rho_{\text{iv}} \rho_{\text{ie}} \textbf{E}_0 \cdot{\langle} \phi_{\text{ir}} \chi_{\text{iv}} | \mu (\textbf{R}) | \phi_{\text{fr}} \chi_{\text{iv}} \rangle \cdot{\langle} \phi_{\text{fr}} \chi_{\text{iv}} | \mu (\textbf{R},t) | \phi_{\text{ir}} \chi_{\text{iv}} \rangle \]

\[ =\sum\limits_{\text{i,f}} \rho_{\text{ir}} \rho_{\text{iv}} \rho_{\text{ie}} \textbf{E}_0 \cdot{\langle} \phi_{\text{ir}} | \mu_{\text{ave.iv}} | \phi_{\text{fr}} | \mu_{\text{ave.iv}}\text{(t)} | \phi_{\text{ir}} \rangle \]

\[ =\sum\limits_{\text{i}} \rho_{\text{ir}} \rho_{\text{iv}} \rho_{\text{ie}} \textbf{E}_0 \cdot{\langle} \phi_{\text{ir}} | \mu_{\text{ave.iv}} \textbf{E}_0 \cdot{\mu}_{\text{ave.iv}}\text{(t)} | \phi_{\text{ir}} \rangle . \]

Al pasar de la segunda a la tercera línea de esta derivación, se utilizó la siguiente identidad:

\[ \langle \phi_{\text{fr}} \chi_{\text{iv}} \psi_{\text{ie}} | \mu \text{(t)} | \phi_{\text{ir}} \chi_{\text{iv}} \psi_{\text{ie}} | e^{\left(\dfrac{\text{iHt}}{\hbar}\right)} \mu e^{\left(-\dfrac{\text{iHt}}{\hbar}\right)} | \phi_{\text{ir}} \chi_{\text{iv}} \psi_{\text{ie}} \rangle \]

\[ =\langle \phi_{\text{fr}} \chi_{\text{iv}} \psi_{\text{ie}} | e^{\left(\dfrac{\text{itH}_{v,r}}{\hbar}\right)} \mu (\textbf{R}) e^{\left(-\dfrac{\text{itH}_{v,r}}{\hbar}\right)} | \phi_{\text{ir}} \chi_{\text{iv}} \psi_{\text{ie}} \rangle , \]

donde H es el hamiltoniano completo (electrónico más vibracional más rotacional) y\(\text{H}_{\text{v,r}}\) es el hamiltoniano vibracional y rotacional para el movimiento en la superficie electrónica del estado\(\psi_{\text{ie}}\) cuyo momento dipolar es\(\mu (\textbf{R})\). De la tercera línea a la cuarta, la separación (aproximada) de los movimientos rotacionales y vibracionales en\(\text{H}_{\text{v,r}}\)

\[ \text{H}_{\text{v,r}} = \text{H}_{\text{v}} + \text{H}_{\text{r}} \]

se ha utilizado junto con el hecho de que\(\chi_{\text{iv}} \text{ is an eigenfunction of } \text{H}_{\text{v}}\):

\[ H_v \chi_{iv} = E_{iv} \chi_{iv} \]

escribir

\[ \langle \chi_{iv} | \mu (\textbf{R},t) | \chi_{iv} \rangle = e^{\left(\dfrac{\text{itH}_r}{\hbar}\right)} \langle \chi_{iv} | e^{\left(\dfrac{\text{itH}_v}{\hbar}\right)} \mu (\textbf{R}) e^{\left(-\dfrac{\text{itH}_v}{\hbar}\right)} | \chi_{iv} \rangle e^{\left(-\dfrac{\text{itH}_r}{\hbar}\right)} \]

\[ = e^{\left( \dfrac{\text{itH}_r}{\hbar} \right)} \langle \chi_{\text{iv}} | e^{\left(\dfrac{\text{itE}_{iv}}{\hbar}\right)} \mu (\textbf{R}) e^{\left(-\dfrac{\text{itE}_{iv}}{\hbar}\right)} | \chi_{iv} \rangle e^{\left(-\dfrac{\text{itH}_{r}}{\hbar}\right)} \]

\[ = e^{\left(\dfrac{\text{itH}_{r}}{\hbar}\right)} \langle \chi_{iv} | \mu (\textbf{R}) | \chi_{iv} \rangle e^{\left(-\dfrac{\text{itH}_{r}}{\hbar}\right)} \]

\[ = \mu_{\text{ave.iv}}\text{(t)}. \]

En efecto,\(\mu\) se sustituye por el momento dipolo electrónico promediado vibracionalmente\(\mu_{\text{ave,iv}}\) para cada estado vibracional inicial que pueda estar involucrado, y la función de correlación de tiempo se convierte así en:

\[ \text{C(t)} = \sum\limits_{\text{i}} \rho_{\text{ir}} \rho_{\text{iv}} \rho_{\text{ie}} \langle \phi_{\text{ir}} | \textbf{E}_0 \cdot{\mu}_{\text{ave, iv}}\text{(t)} | \phi_{\text{ir}} \rangle , \]

donde\(\mu_{\text{ave, iv}}\text{(t)}\) es el momento dipolo promediado para el estado vibracional\(\chi_{\text{iv}}\) en el tiempo t, dado que fue\(\mu_{\text{ave, iv}}\) en el tiempo t = 0. La dependencia del tiempo\(\mu_{\text{ave, iv}}\text{(t)}\) es inducida por el hamiltoniano rotacional\(\text{H}_r\), como se muestra claramente en los pasos detallados anteriormente:

\[ \mu_{\text{ave, iv}}\text{(t)} = e^{\left( \dfrac{\text{itH}_r}{\hbar} \right)} \langle \chi_{\text{iv}} | \mu (\textbf{R}) | \chi_{text{iv}} \rangle e^{\left(-\dfrac{\text{itH}_r}{\hbar}\right)}. \]

En este caso particular, el promedio de equilibrio se toma sobre los estados rotacionales iniciales cuyas probabilidades se denotan\(\rho_{\text{ir}}\), cualquier estado vibracional inicial que pueda ser poblado, con probabilidades\(\rho_{\text{iv}}\), y cualquier estado electrónico poblado, con probabilidades\(\rho_{\text{ie}}\).

transiciones vibración-rotación

Para las transiciones de vibración-rotación dentro de un solo estado electrónico, los estados electrónicos inicial y final son los mismos, pero los estados vibracionales y rotacionales inicial y final difieren. Como resultado, la suma sobre los estados finales contenida en la expresión\( \sum\limits_{i,f} \phi_i \textbf{E}_0 \cdot{\langle}\Phi_i | \mu | \Phi_f \rangle \textbf{E}_0 \cdot{\langle} | \mu | \Phi_i \rangle e^{i(\omega_{f,i})t} \) se aplica únicamente a la suma sobre los estados vibracionales y rotacionales finales. Paralelamente al desarrollo realizado en el caso de rotación pura dado anteriormente, esto se puede mostrar de la siguiente manera:

\[ \sum\limits_{i,f} \rho_i \textbf{E}_0 \cdot{\langle} \Phi_i | \mu | \Phi_f \rangle \textbf{E}_0 \cdot{\langle} | \mu \text{(t) }| \Phi_i \rangle \]

\[ = \sum\limits_{i,f} \rho_i\textbf{E}_0 \cdot{\langle}\phi_{\text{ir}} \chi_{\text{iv}} \psi_{\text{ie}} | \mu | \phi_{\text{fr}} \chi_{\text{fv}} \psi_{\text{ie}} \rangle \textbf{E}_0 \cdot{\langle} \phi_{\text{fr}} \chi_{\text{fv}} \psi_{\text{ie}} | \mu \text{(t) }| \phi_{\text{ir}} \chi_{\text{iv}} \psi_{\text{ie}} \rangle \]

\[ = \sum\limits_{i,f} \rho_{\text{ir}} \rho_{\text{iv}} \rho_{\text{ie}} \textbf{E}_0 \cdot{\langle}\phi_{\text{ir}} \chi_{\text{iv}} | \mu (\textbf{R}) | \phi_{\text{fr}} \chi_{\text{fv}} \rangle \textbf{E}_0 \cdot{\langle} \phi_{\text{fr}} \chi_{\text{fv}} | \mu (\textbf{R},t)| \phi_{\text{ir}} \chi_{\text{iv}} \rangle \]

\[ = \sum\limits_{i,f} \rho_{\text{ir}} \rho_{\text{iv}} \rho_{\text{ie}} \textbf{E}_0 \cdot{\langle}\phi_{\text{ir}} \chi_{\text{iv}} | \mu (\textbf{R}_e) + \sum\limits_a (R_a - R_{a, eq}) \dfrac{\partial \mu}{\partial R_a} | \phi_{\text{fr}} \chi_{\text{fv}} \rangle \textbf{E}_0 \cdot{\langle} \phi_{\text{fr}} \chi_{\text{fv}} | e^{\left(\dfrac{\text{itH}_r}{\hbar}\right)}\left( \mu (\textbf{R}_e) + \sum\limits_a(R_a - R_{a, eq}) \dfrac{\partial \mu}{\partial R_a} \right) e^{\left(-\dfrac{\text{itH}_r}{\hbar}\right)} | \phi_{\text{ir}} \chi_{\text{iv}} \rangle e^{\left(i\omega_{fv, iv}t\right)} \]

\[ \sum\limits_{i,f} \rho_{\text{ir}} \rho_{\text{iv}} \rho_{\text{ie}} \langle \phi_{\text{ir}} | \textbf{E}_0 \cdot{\mu_{\text{i,f}}}(\textbf{R}_e)\textbf{E}_0 \cot{\mu_{\text{i,f}}}(\textbf{R}_e,t) | \phi_{\text{ir}} \rangle | \langle \chi_{\text{iv}} | \chi_{\text{fv}} |^2 e^{i\omega_{\text{fv, iv}}t + i\Delta E_{\text{i,f}}\dfrac{t}{\hbar}}, \]

donde

\[ \mu_{\text{i,f}}(\textbf{R}_e,t) = e^{\left( \dfrac{\text{itH}_r}{\hbar} \right)} \mu_{\text{i,f}}(\textbf{R}_e) e^{\left( -\dfrac{\text{itH}_r}{\hbar} \right)} \]

es el elemento de matriz dipolo de transición electrónica, evaluado en la geometría de equilibrio del estado absorbente, que deriva su dependencia del tiempo del hamiltoniano rotacional\(\text{H}_r\) como en las funciones de correlación temporal tratadas anteriormente.

Este desarrollo conduce así a la siguiente definición de C (t) para el caso electrónico, de vibración y de rotación:

\[ \text{C(t)} = \sum\limits_{\text{i,f}} \rho_{\text{ir}} \rho_{\text{iv}} \rho_{\text{ie}} \langle \phi_{\text{ir}} | \textbf{E}_0 \cdot{\mu_{\text{if}}}(\textbf{R}_e)\textbf{E}_0 \cdot{\mu_{\text{if}}}(\textbf{R}_e,t) | \phi_{\text{ir}} \rangle | \langle \chi_{\text{iv}} | \chi_{\text{fv}} \rangle |^2 e^{\left( i\omega_{\text{fv, iv}}t + \dfrac{i\Delta E_{\text{i,f}}t}{\hbar} \right)} \]

pero la tasa neta de absorción de fotones sigue siendo:

\[ \text{R}_{\text{eq.ave.net}} = \left(\dfrac{1}{\hbar^2}\right)\left( 1 - e^{\left( -\dfrac{\hbar \omega}{kT} \right)} \right) \int\limits g(\omega ) I (\omega )\text{ d}\omega . \]

Aquí, I (\(\omega \)) es la transformada de Fourier del C (t) anterior y\(\Delta E_{\text{i,f}}\) es la diferencia de energía electrónica adiabática (es decir, la diferencia de energía entre el nivel v = 0 en el estado electrónico final y el nivel v = 0 en el estado electrónico inicial) para la transición electrónica de interés. El C (t) anterior contiene claramente factores Franck-Condon así como dependencia del tiempo

\[ e^{\left( it\omega_{\text{fv, iv}} + i\Delta E_{\text{i,f}}\dfrac{t}{\hbar} \right)} \]

que produce picos de\( \delta \) función en cada frecuencia de transición electrónica-vibracional y dependencia del tiempo de rotación contenida en la cantidad de función de correlación de tiempo

\[ \langle \phi_{\text{ir}} \textbf{E}_0 \cdot{\mu_{\text{i,f}}} (\textbf{R}_e)\textbf{E}_0\cdot{\mu_{\text{i,f}}}(\textbf{R}_e,t) |\phi_{\text{ir}} \rangle . \]

En resumen, la función de forma de línea I (\(\omega \)) produce la tasa neta de absorción de fotones

\[ R_{\text{eq.ave.net}} = \left( \dfrac{1}{\hbar^2} \right)\left( 1 - e^{\left(-\dfrac{\hbar \omega}{kT}\right)}\right) \int\limits g(\omega ) I(\omega )\text{ d}\omega \]

en todos los casos anteriores, e I (\( \omega \)) es la transformada de Fourier de una función C (t) dependiente del tiempo correspondiente en todos los casos. Sin embargo, los casos de rotación pura, vibración-rotación y rotación electrónica difieren en la forma de sus respectivas C (t).

\[ \text{C(t)} = \sum\limits_i \rho_{\text{ir}} \rho_{\text{iv}} \rho_{\text{ie}} \langle \phi_{\text{ir}} | (\textbf{E}_0 \cdot{\mu}_{\text{ave, iv}} ) \textbf{E}_0 \cdot{\mu}_{\text{ave, iv}}(t) | \phi_{\text{ir}} \rangle \]

en el caso rotacional puro,

\[ \text{C(t)} = \sum\limits_i \rho_{\text{ir}} \rho_{\text{iv}} \rho_{\text{ie}} \langle \phi_{\text{ir}} | (\textbf{E}_0 \cdot{\mu}_{\text{trans}} ) \textbf{E}_0 \cdot{\mu}_{\text{trans}}(t) | \phi_{\text{ir}} \rangle e^{it\omega_{\text{fv, iv}}} \]

en el caso de rotación de vibración electrónica.

Todas estas funciones de correlación temporal contienen dependencias de tiempo que surgen del movimiento rotacional de un vector relacionado con dipolo (es decir, el dipolo promediado vibracionalmente\(\mu_{\text{ave, iv}}(t)\), el dipolo\(\mu_{\text{trans}}(t)\) de transición vibracional o el dipolo de transición electrónico\(\mu_{\text{i,f}}(\textbf{R}_{\text{e,t}})\)) y los dos últimos también contienen dependencias oscilatorias del tiempo (es decir,\( e^{\left( it\omega_{fv,iv} \right)}\) o\(e^{\left( it\omega_{fv,iv} + i\Delta E_{\text{i,f}}\frac{t}{\hbar} \right)} \)) que surgen de diferencias de nivel de energía vibracional o electrónica-vibracional. En los tratamientos de las siguientes secciones se considera las contribuciones rotacionales en circunstancias que caracterizan, por ejemplo, muestras gaseosas diluidas donde la frecuencia de colisión es baja y muestras en fase líquida donde el movimiento rotacional se describe mejor en términos de movimiento difusional.

Mecanismos de ampliación de líneas

Si se supone que el movimiento de rotación de las moléculas está completamente libre de obstáculos (por ejemplo, por cualquier entorno o por colisiones con otras moléculas), es apropiado expresar la dependencia del tiempo de cada una de las funciones de correlación de tiempo dipolo enumeradas anteriormente en términos de un modelo de “rotación libre”. Por ejemplo, cuando se trata de moléculas diatómicas, el C (t) electrónicovibracional-rotacional apropiado para una transición electrónica-vibracional específica se convierte en:

\[ \text{C(t)} = \left( \dfrac{1}{\text{q}_r\text{q}_v\text{q}_e\text{q}_t}\right) \sum\limits_J (2J+1) e^{\left( -\dfrac{-h^2J(J+1)}{8\pi^2IkT} \right)}e^{\left( -\dfrac{hv_{\text{vib}}vi}{kT} \right)}g_{ie} \langle \phi_J | \text{E}_0 \cdot{\mu}_{\text{i,f}}(\textbf{R}_e)\textbf{E}_0\cdot{\mu}_{\text{ie}}(\textbf{R}_e,t) | \phi_J \rangle | \langle \chi_{\text{iv}} | \chi_{\text{fv}} \rangle |^2 e^{\left( ithv_{\text{vib}} + i\Delta E_{\text{i,f}}\dfrac{t}{\hbar} \right)}. \]

Aquí,

\[ \text{q}_r = \left( \dfrac{8\pi^2 IkT}{h^2} \right) \]

es la función de partición rotacional (siendo I el momento de inercia de\(I = \mu R_e^2, \text{ and } \dfrac{h^2J(J+1)}{8\pi^2I}\) la molécula la energía rotacional de la molécula para el estado con número cuántico J y degeneración 2J+1)

\[ \text{q}_v = \dfrac{ e^{\left( -\dfrac{hv_{\text{vib}}}{2\text{kT}} \right)} }{1 - e^{\left( -\dfrac{hv_{\text{vib}}}{\text{kT}}\right) } } \]

es la función de partición vibracional (\(v_{\text{vib}}\)siendo la frecuencia vibracional),\(\text{g}_{\text{ie}}\) es la degeneración del estado electrónico inicial,

\[ \text{q}_t = \sqrt[3]{\left( \dfrac{2\pi \text{mkT}}{h^2} \right)}V \]

es la función de partición vibracional (\(v_{\text{vib}}\)siendo la frecuencia vibracional),\(\text{g}_{\text{ie}}\) es la degeneración del estado electrónico inicial,

\[ \text{q}_t = \sqrt[3]{\dfrac{2\pi mkT}{h^2}}\text{V} \]

es la función de partición traslacional para las moléculas de masa m que se mueven en el volumen V, y\(\Delta E_{\text{i,f}}\) es el espaciamiento de energía electrónica adiabática.

Las funciones\( \langle \phi_J | \textbf{E}_0 \cdot{\mu}_{\text{i,f}}(\textbf{R}_e)\textbf{E}_0 \cdot{\mu}_{\text{i,f}}(\textbf{R}_e,t) | \phi_J \rangle \) describen la evolución temporal del vector relacionado con dipolo (el dipolo de transición electrónico en este caso) para el estado rotacional J. En un modelo de “rotación libre”, esta función se toma como la forma:

\[ \langle \phi_J | \textbf{E}_0 \cdot{\mu}_{\text{i,f}}(\textbf{R}_e)\textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e,t) \phi_J \rangle = \langle \phi_J | \textbf{E}_0 \cdot{\mu}_{\text{i,f}}(\textbf{R}_e)\textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e,0) \phi_J \rangle \text{Cos}\left( \dfrac{\text{hJ(J + 1)}}{4\pi\text{I}} \right) \]

donde

\[ \omega_J = \left( \dfrac{\text{hJ(J + 1)}}{4\pi\text{I}} \right) \]

es la frecuencia rotacional (en ciclos por segundo) para la rotación de la molécula en el estado marcado por J. Esta dependencia oscilatoria del tiempo, combinada con la dependencia del\( e^{\left( it\omega_{\text{fv,iv}} + i\Delta E_{\text{i,f}} \frac{t}{\hbar} \right)} \) tiempo que surge de los factores electrónicos y vibracionales, producen, cuando esta función C (t) es transformada de Fourier para generar I ( \(\omega \)) una serie de\(\delta\) -función “picos” siempre que

\[ \omega = \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \]

Las intensidades de estos picos se rigen por el

\[ \text{C(t)} = \left( \dfrac{1}{\text{q}_r\text{q}_v\text{q}_e\text{q}_t}\right) \sum\limits_J (2J+1) e^{\left( -\dfrac{-h^2J(J+1)}{8\pi^2IkT} \right)}e^{\left( -\dfrac{hv_{\text{vib}}vi}{kT} \right)}g_{ie}. \]

Factores poblacionales de Boltzmann así como por los factores\( | \langle \chi_{iv}| \chi_{fv} \rangle |^2\) Franck-Condon y los\(\langle \phi_J | \textbf{E}_0 \cdot{\mu}_{\text{i,f}}(\textbf{R}_e)\textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e,0) | \phi_J \rangle \) términos.

Este mismo análisis se puede aplicar a las dependencias de tiempo de rotación pura y vibración-rotación C (t) con resultados análogos. En el primero, se prevé que los picos de\(\delta \) función -ocurran en

\[ \omega \pm \omega_J \]

y en este último en

\[ \omega = \omega_{\text{fv,iv}} \pm \omega_J ; \]

con las intensidades gobernadas por los factores independientes del tiempo en las expresiones correspondientes para C (t).

En las mediciones experimentales, tales\(\delta\) picos agudos de función, por supuesto, no se observan. Incluso cuando se utilizan fuentes de luz láser de ancho de banda muy estrecho (es decir, para las cuales g (\(\omega \)) es una función de pico extremadamente estrecho), se encuentra que las líneas espectrales poseen anchuras finitas. Discutamos ahora varias fuentes de ampliación de líneas, algunas de las cuales se relacionarán con desviaciones del modelo de movimiento rotacional “sin obstáculos” introducido anteriormente.

Ampliamiento Doppler

En las expresiones anteriores para\(C(t)\), se muestra explícitamente el promedio sobre los estados rotacionales, vibracionales y electrónicos iniciales. También hay un promedio sobre el movimiento traslacional implícito en todas estas expresiones. Su papel no se ha enfatizado (todavía) porque los niveles de energía molecular, cuyos espaciamientos producen las frecuencias características a las que la luz puede ser absorbida o emitida, no dependen del movimiento traslacional. Sin embargo, la frecuencia del campo electromagnético que experimentan las moléculas en movimiento sí depende de las velocidades de las moléculas, por lo que ahora se debe abordar este tema.

Las clases elementales de física expresan el llamado desplazamiento Doppler de la frecuencia de una onda inducida por el movimiento ya sea de la fuente de luz o de la molécula (Einstein nos dice que estos dos puntos de vista deben dar resultados idénticos) de la siguiente manera:

\[ \omega_{\text{observed}} = \omega_{\text{nominal}} \left(\dfrac{1}{1+\dfrac{v_z}{c}}\right) \approx \left( 1 - \dfrac{v_z}{c} + ...\right) . \]

Aquí,\(\omega_{\text{nominal}}\) es la frecuencia de la fuente de luz inmóvil vista por las moléculas inmóviles,\(v_z\) es la velocidad del movimiento relativo de la fuente de luz y las moléculas, c es la velocidad de la luz, y\(\omega_{\text{observed}}\) es la frecuencia desplazada Doppler (es decir, la frecuencia vista por las moléculas). La segunda identidad se obtiene expandiendo, en una serie de potencias, el\(\left(1 + \dfrac{v_z}{c}\right)^{-1}\) factor, y es válido en forma truncada cuando las moléculas se mueven con velocidades significativamente por debajo de la velocidad de la luz.

Para todos los casos considerados anteriormente, una función C (t) se somete a transformación de Fourier para obtener una función espectral de forma de línea I (\(\omega\)), que luego proporciona el ingrediente esencial para calcular la tasa neta de absorción de fotones. En este proceso de transformada de Fourier,\(\omega\) se supone que la variable es la frecuencia del campo electromagnético experimentado por las moléculas. Las consideraciones anteriores del desplazamiento Doppler llevan entonces a uno a darse cuenta de que la forma funcional correcta a utilizar en la conversión de C (t) a I (\(\omega\)) es:

\[ I(\omega ) = \int C(t) e^{-t\omega \left( 1 - \dfrac{v_z}{c} \right)} \text{dt} ,\]

donde\(\omega \) es la frecuencia nominal de la fuente de luz.

Como se indicó anteriormente, dentro de C (t) también hay un promedio de equilibrio sobre el movimiento traslacional de las moléculas. Para una muestra en fase gaseosa sometida a colisiones aleatorias y en equilibrio térmico, este promedio se caracteriza por la conocida distribución de velocidad Maxwell-Boltzmann:

\[ \sqrt{\left( \dfrac{m}{2\pi kT} \right)^3} e^{\left( \dfrac{-m\left( v_x^2 + v_y^2 + v_z^2 \right)}{2kT}\right)}dv_x dv_y dv_z .\]

Aquí m es la masa de las moléculas y\(v_x, v_y, \text{ and }v_z\) etiquetar las velocidades a lo largo de las coordenadas cartesianas fijas de laboratorio.

Definir el eje z como la dirección de propagación de los fotones de la luz y llevar a cabo el promedio del factor Doppler sobre dicha distribución de velocidad, se obtiene:

\[ \int\limits_{-\infty}^{\infty} e^{-it\omega \left( 1- \dfrac{v_z}{c} \right)} \sqrt{\left( \dfrac{m}{2\pi kT} \right)^3} e^{\left( \dfrac{-m(v_x^2 + v_y^2 + v_z^2)}{2kT} \right)}dv_x dv_y dv_z \]

\[ = e^{-\omega t} \int\limits_{-\infty}^{\infty}\sqrt{\dfrac{m}{2\pi kT}}e^{\left(\dfrac{i\omega tv_z}{c}\right)} e^{\left( \dfrac{-mv_z}{2kT} \right)} dv_z \]

\[ =e^{-\omega t} e^{\left( \dfrac{-\omega^2t^2kT}{2mc^2} \right)} \]

Este resultado, cuando se sustituye en las expresiones para C (t), produce expresiones idénticas a las dadas para los tres casos tratados anteriormente pero con una modificación. El promedio de movimiento traslacional ya no necesita ser considerado en cada C (t); en cambio, las expresiones anteriores para C (t) deben multiplicarse cada una por un factor\( e^{\frac{-\omega^2 t^2kT}{2mc^2}} \) que encarna el desplazamiento Doppler promediado traduccionalmente. La función de forma de línea espectral I (\(\omega\)) se puede obtener entonces para cada C (t) simplemente transformando Fourier:

\[ I(\omega) = \int\limits_{-\infty}^{\infty} e^{-i\omega t}C(t)\text{dt}. \]

Cuando se aplica a los casos de rotación, vibración-rotación o vibración-rotación electrónica dentro del modelo de rotación “sin obstáculos” tratado anteriormente, la transformada de Fourier involucra integrales de la forma:

\[ I(\omega) = \int\limits_{-\infty}^{\infty} e^{-\omega t}e^{\dfrac{-\omega^2 t^2kT}{2mc^2}}e^{it \left(\omega_{\text{fv,iv}} + \Delta \dfrac{E_{\text{i,f}}}{\hbar} \pm \omega_J \right)} \text{dt}.\]

Esta integral surgiría en el caso electrónico-vibración-rotación; los otros dos casos implicarían integrales de la misma forma pero con la\( \frac{\Delta E_{\text{i,f}}}{\hbar} \) ausencia en la situación de vibración-rotación y con\(\omega_{\text{fv, iv}} + \frac{\Delta E_{\text{i,f}}}{\hbar}\) faltantes para transiciones de rotación pura. Todas estas integrales se pueden llevar a cabo analíticamente y producir:

\[ I(\omega ) = \sqrt{\dfrac{2mc^2\pi}{\omega^2 kT}}e^{\left( \dfrac{-\left(\omega - \omega_{\text{fv, iv}} - \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J\right)^2 mc^2}{2\omega^2 kT} \right)}. \]

El resultado es una serie de “picos” gaussianos en\(\omega\) el espacio, centrados en:

\[ \omega = \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \]

con anchuras (\(\sigma)\)determinadas por

\[ \sigma^2 = \dfrac{\omega^2kT}{mc^2}, \]

dada la temperatura\(T\) y la masa de las moléculas\(m\). Cuanto más caliente es la muestra, más rápido se mueven las moléculas en promedio, y más amplia es la distribución de las frecuencias Doppler desplazadas experimentadas por estas moléculas. El resultado neto del efecto Doppler es producir una función de forma de línea que es similar a la serie de\(\delta\) funciones del modelo de rotación “sin obstáculos” pero con cada pico\(\delta\) de función ensanchado en una forma gaussiana

Amplamiento de Presión

Para incluir los efectos de las colisiones en la parte de movimiento rotacional de cualquiera de las funciones C (t) anteriores, se debe introducir un modelo de cómo tales colisiones cambian los vectores dipolerelados que entran en C (t). El modelo más elemental utilizado para abordar colisiones se aplica a muestras gaseosas que se supone que experimentan un movimiento rotacional sin obstáculos hasta ser golpeadas por otra molécula, momento en el que se aplica una “patada” aleatoria al vector dipolo y después de lo cual la molécula vuelve a su movimiento rotacional sin obstáculos.

Los efectos de tales patadas inducidas por colisión se tratan dentro del modelo denominado ensanchamiento de presión (a veces llamado ensanchamiento colisional) modificando la función de correlación de rotación libre mediante la introducción de un factor de amortiguación exponencial \(e^{\frac{-|t|}{\tau}}\): Se supone que el parámetro\(\tau\) de escala de tiempo de

\[ \langle \phi_J | \textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e)\textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e,0) | \phi_J\rangle Cos \left( \dfrac{hJ(J+1)t}{4\pi I} \right) \]

\[ \rightarrow \langle \phi_J | \textbf{E}_0 \cdot{\mu}_{\text{i,f}}(\textbf{R}_e)\textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e,0) | \phi_J\rangle Cos\left( \dfrac{hJ(J+1)t}{4\pi I} \right) e^{\dfrac{-|t|}{\tau}}. \]

esta función de amortiguación caracteriza el tiempo promedio entre colisiones y, por lo tanto, debe ser inversamente proporcional a la colisión frecuencia. Su magnitud también está relacionada con la efectividad con la que las colisiones hacen que la función dipolo se desvíe de su movimiento rotacional sin obstáculos (es decir, relacionado con la fuerza de colisión). En efecto, la amortiguación exponencial hace que la función\( \langle \phi_J | \textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e)\textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e,t)|\phi_J\rangle \) de correlación de tiempo “pierda su memoria” y disminuya a cero; este punto de vista de “memoria” se basa en la visualización\( \langle \phi_J | \textbf{E}_0 \cdot{\mu}_{\text{i,f}}(\textbf{R}_e)\textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e,t) | \phi_J\rangle \) como proyección\( \textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e,t) \) a lo largo de su valor\( \textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e,0) \) t=0 en función del tiempo t.

Introducir esta dependencia adicional del\( e^{\frac{-|t|}{\tau}} \) tiempo en C (t) produce, cuando C (t) es transformada de Fourier para generar I (\(\omega\)),

\[ I(\omega ) = \int\limits_{-\infty}^{\infty}e^{-i\omega t}e^{\dfrac{-|t|}{\tau}}e^{\dfrac{-\omega^2 t^2kT}{2mc^2}}e^{it\left( \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right)}\text{dt} . \]

En el límite del ensanchamiento Doppler muy pequeño, el\( \frac{\omega^2t^2kT}{2mc^2} \) factor puede ignorarse (es decir,\( e^{\frac{-\omega^2t^2kT}{2mc^2}} \) establecer igual a la unidad), y

\[ I(\omega) = \int\limits_{-\infty}^{\infty}e^{-i\omega t}e^{-\left(\dfrac{|t|}{\tau}\right)}e^{\left( it\left( \omega_{\text{fv,iv}}+\dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right)\right)} \text{dt} \]

resultados. Esta integral se puede realizar analíticamente y genera:

\[ I(\omega) = \dfrac{1}{4\pi}\left( \dfrac{\dfrac{1}{\tau}}{\left( \dfrac{1}{\tau} \right)^2 + \left( \omega - \omega_{\text{fv,iv}} -\dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J\right)^2} + \dfrac{\dfrac{1}{\tau}}{\left( \dfrac{1}{\tau} \right)^2 + \left( \omega + \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right)^2} \right) \]

un par de picos lorentzianos en\(\omega\) -espacio centrados nuevamente en

\[ \omega = \pm \left[ \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right]. \]

El ancho completo a media altura de estos picos lorentzianos es\(\frac{2}{\tau}\). Se dice que los picos individuales se han ampliado de presión o colisionalmente.

Cuando no se puede descuidar el ensanchamiento Doppler en relación con el ensanchamiento colisional, la integral anterior

\[ I(\omega) = \int\limits_{-\infty}^{\infty}e^{-\omega t}e^{-\dfrac{|t|}{\tau}}e^{-\dfrac{\omega^2t^2kT}{2mc^2}}e^{\left(it \left( \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right) \right)} \text{dt}\]

es más difícil de realizar. Sin embargo, se puede llevar a cabo y nuevamente produce una serie de picos centrados en

\[ \omega = \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \]

pero cuyas anchuras están determinadas tanto por Doppler como por efectos de ensanchamiento de presión. Por lo tanto, las formas de línea resultantes ya no son puramente lorentzianas ni gaussianas (que se comparan en la siguiente figura para ambas funciones que tienen el mismo ancho completo a media altura y la misma área integrada), sino que tienen una forma que se llama forma Voight.

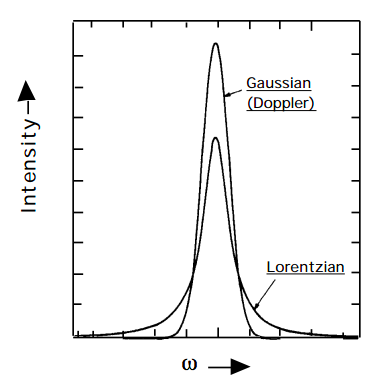
Figura 15.4.1: ¡Inserta el subtítulo aquí!

Ampliamiento de Difusión Rotacional

Las moléculas en líquidos y gases muy densos experimentan frecuentes colisiones con las otras moléculas; es decir, el tiempo medio entre colisiones es corto en comparación con el período de rotación para su rotación sin obstáculos. Como resultado, la dependencia del tiempo de la función de correlación relacionada con el dipolo ya no se puede modelar en términos de rotación libre que es interrumpida por colisiones (infrecuentes) y desplazamiento de Dopler. En cambio, se vuelve apropiado un modelo que describa el incesante ataque del dipolo de la molécula por las moléculas circundantes. Para muestras líquidas en las que estas colisiones frecuentes hacen que el dipolo de la molécula experimente movimientos angulares que cubren todos los ángulos (es decir, en contraste con un vidrio congelado o sólido en el que el dipolo de la molécula sufriría un movimiento pendular fuertemente perturbado alrededor de alguna orientación favorecida), el llamado a menudo se utiliza el modelo de difusión rotacional. En esta imagen, la parte dependiente de rotación de C (t) se expresa como:

\[ \langle \phi_J | \textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e)\textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e,t)|\phi_J\rangle = \langle \phi_J | \textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e)\textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e,0) |\phi_J\rangle e^{-2D_{\text{rot}}|t|}, \]

donde D\(_{\text{rot}}\) es la constante de difusión rotacional cuya magnitud detalla la disminución del tiempo en el valor promedio de\( \textbf{E}_0\cdot{\mu}_{\text{i,f}}(\textbf{R}_e,t)\) en el tiempo t con respecto a su valor en el tiempo t = 0; cuanto mayor D\(_{\text{rot}}\), más rápido es este decaimiento.

Al igual que con el ensanchamiento de presión, esta dependencia exponencial del tiempo, cuando se somete a transformación de Fourier, produce:

\[ I(\omega) = \int\limits^{\infty}_{-\infty}e^{-i\omega t}e^{-2D_{\text{rot}}|t|}e^{\dfrac{-\omega^2t^2kT}{2mc^2}}e^{\left(it \left( \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right) \right)}\text{dt}. \]

De nuevo, en el límite de ensanchamiento Doppler muy pequeño, el\( \frac{\omega^2t^2kT}{2mc^2} \) factor puede ser ignorado (es decir,\( e^{-\frac{\omega^2t^2kT}{2mc^2}} \)) conjunto igual a la unidad), y

\[ I(\omega) = \int\limits_{-\infty}^{\infty}e^{-i\omega t}e^{-2D_{\text{rot}}|t|}e^{\left(it \left( \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right) \right)} \text{dt} \]

resultados. Esta integral se puede evaluar analíticamente y genera:

\[ I(\omega) = \dfrac{1}{4\pi}\left( \dfrac{2D_{\text{rot}}}{(2D_{\text{rot}})^2 + \left( \omega -\omega_{\text{fv,iv}} - \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right)^2} + \dfrac{2D_{\text{rot}}}{(2D_{\text{rot}})^2 + \left( \omega + \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right)^2} \right), \]

un par de picos lorentzianos en\(\omega\) -espacio centrados nuevamente en

\[ \omega = \pm \left[ \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right]. \]

El ancho completo a media altura de estos picos lorentzianos es 4D\(_{\text{rot}}\). En este caso, se dice que los picos individuales se han ampliado a través de la difusión rotacional. Cuando no se puede descuidar el ensanchamiento Doppler en relación con el ensanchamiento colisional, la integral anterior

\[ I(\omega) = \int\limits_{-\infty}^{\infty}e^{-i\omega t}e^{-2D_{\text{rot}}|t|}e^{-\dfrac{\omega^2t^2kT}{2mc^2}}e^{\left(it \left( \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right) \right)} \text{dt.} \]

es más difícil de realizar. Sin embargo, se puede llevar a cabo y nuevamente produce una serie de picos centrados en

\[ \omega = \pm \left[ \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right] \]

pero cuyas anchuras están determinadas tanto por los efectos Doppler como por los efectos de difusión rotacional.

Ampliamiento homogéneo de por vida o Heisenberg

Siempre que la especie absorbente sufre uno o más procesos que agotan su número, decimos que tiene una vida finita. Por ejemplo, una especie que sufre disociación unimolecular tiene una vida finita, al igual que un estado excitado de una molécula que decae por emisión espontánea de un fotón. Cualquier proceso que agote la especie absorbente aporta otra fuente de dependencia del tiempo para las funciones de correlación temporal dipolo C (t) discutidas anteriormente. Esta dependencia del tiempo suele modelarse añadiendo, de manera multiplicativa, un factor\( e^{-\frac{|t|}{\tau}} \). Esto, a su vez modifica la función de forma de línea I (\(\omega\)) de una manera muy parecida a la discutida al tratar el caso de difusión rotacional:

\[ I(\omega) = \int\limits_{-\infty}^{\infty}e^{-i\omega t}e^{-\dfrac{|t|}{\tau}}e^{-\dfrac{\omega^2t^2kT}{2mc^2}}e^{\left( it\left( \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right) \right)} \text{dt}. \]

No es sorprendente que cuando la contribución Doppler es pequeña, se obtiene:

\[ I(\omega) = \dfrac{1}{4\pi} \left( \dfrac{\dfrac{1}{\tau}}{\left(\dfrac{1}{\tau}\right)^2 \left( \omega - \omega_{\text{fv,iv}} - \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right)^2 } + \dfrac{\dfrac{1}{\tau}}{\left( \dfrac{1}{\tau} \right)^2 + \left( \omega + \omega_{\text{fv,iv}} + \dfrac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \right)^2} \right). \]

En estas líneas lorentzianas, el parámetro\(\tau\) describe la vida útil de decaimiento cinético de la molécula. Se dice que las líneas espectrales han sido de por vida o Heisenberg ampliadas en una cantidad proporcional a\(\frac{1}{\tau}\). Esta última terminología surge porque la vida finita de los estados moleculares puede ser vista como productora, a través de la relación de incertidumbre de Heisenberg\( \Delta E\Delta t > \hbar \), estados cuya energía es “incierta” dentro de una cantidad\(\Delta\) E.

Amplamiento no homogéneo del sitio

Entre los mecanismos de ampliación de la línea anterior, la presión, la difusión rotacional y los ensanchamientos de vida son todos de la variedad homogénea. Esto significa que cada molécula de la muestra se ve afectada exactamente de la misma manera por el proceso de ampliación. Por ejemplo, no se encuentran algunas moléculas con vidas cortas y otras con vidas largas, en el caso Heisenberg; todo el conjunto de moléculas se caracteriza por una sola vida.

En contraste, el ensanchamiento Doppler es de naturaleza no homogénea porque cada molécula experimenta un ensanchamiento que es característico de su naturaleza particular (velocidad\(v_z\) en este caso). Es decir, las moléculas rápidas tienen sus líneas ensanchadas más que las moléculas más lentas. Otro ejemplo importante de ensanchamiento no homogéneo es proporcionado por el llamado ensanchamiento del sitio. Las moléculas embebidas en un líquido, sólido o vidrio no experimentan exactamente las mismas interacciones con su entorno en el instante de la absorción de fotones. “La distribución de ambientes instantáneos de “" solvatación "” puede ser bastante “" estrecha "” (por ejemplo, en una matriz sólida altamente ordenada) o bastante “" amplia "” (por ejemplo, en un líquido a alta temperatura).” Diferentes ambientes producen diferentes divisiones de nivel de energía

\[ \omega = \omega_{\text{fv,iv}} + \frac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J \]

porque los estados inicial y final están “solvatados” de manera diferente por el entorno y por lo tanto diferentes frecuencias a las que puede ocurrir la absorción de fotones. La distribución de las divisiones del nivel de energía hace que la muestra se absorba en un rango de frecuencias como se ilustra en la siguiente figura donde se comparan formas de líneas homogéneas y no homogéneas.

Figura 15.4.2: ¡Inserta el subtítulo aquí!

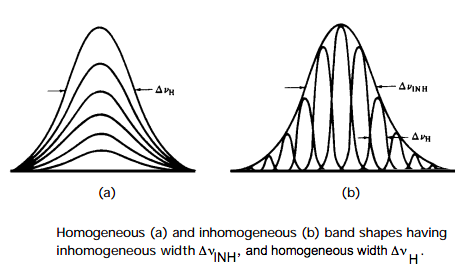
La función de forma de línea espectral I (\(\omega\)) se amplía aún más cuando la inhomogeneidad del sitio está presente y es significativa. Estos efectos pueden modelarse convolucionando el tipo de función I (\(\omega\)) que resulta del Doppler, la vida útil, la difusión rotacional y el ensanchamiento de presión con una distribución Gaussiana P (\(\Delta E\)) que describe la distribución no homogénea de las divisiones del nivel de energía:

\[ I(\omega) = \int\limits I^0(\omega ;\Delta E) P(\Delta E) d\Delta E. \]

Aquí I\(^0(\omega ;\Delta E)\) es una función de forma de línea como las descritas anteriormente cada una de las cuales contiene un conjunto de frecuencias (por ejemplo,\( \omega = \omega_{\text{fv,iv}} + \frac{\Delta E_{\text{i,f}}}{\hbar} \pm \omega_J = \omega + \frac{\Delta E}{\hbar})\) en las que ocurre la absorción o emisión.

Una prueba experimental común para el ensanchamiento no homogéneo implica la quema de agujeros. En tales experimentos, una fuente de luz intensa (a menudo un láser) se sintoniza a una frecuencia\(\omega_{\text{burn}}\) que se encuentra dentro de la línea espectral que se sondea para un ensanchamiento no homogéneo. Después, se utiliza una segunda fuente de luz sintonizable para escanear a través del perfil de la línea espectral, y, por ejemplo, se registra un espectro de absorción. Dado un perfil de absorción como se muestra a continuación en ausencia de la fuente de luz de combustión intensa:

Figura 15.4.3: ¡Inserta el subtítulo aquí!

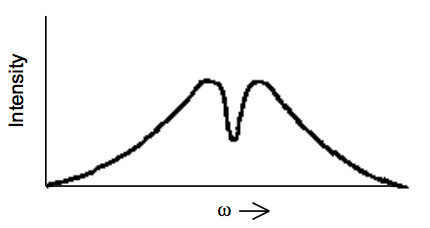
uno espera ver un perfil como el que se muestra a continuación:

Figura 15.4.4: ¡Inserta el subtítulo aquí!

si el ensanchamiento no homogéneo es operativo.

La interpretación del cambio en el perfil de absorción causado por la fuente de luz brillante procede de la siguiente manera:

1. En el conjunto de moléculas contenidas en la muestra, algunas moléculas absorberán a o cerca de la frecuencia de la fuente de luz brillante\(\omega_{\text{burn}}\); otras moléculas (aquellas cuyos ambientes no producen divisiones de nivel de energía que coincidan\(\omega_{\text{burn}}\)) no absorberán a esta frecuencia.
2. Aquellas moléculas que absorben a\(\omega_{\text{burn}}\) voluntad tienen su transición saturada por la fuente de luz intensa, lo que hace que esta región de frecuencia del perfil lineal sea transparente para una mayor absorción.
3. Cuando la fuente de luz “sonda” se escanea sobre el perfil lineal, inducirá absorciones para aquellas moléculas cuyos entornos locales no permitieron que fueran saturadas por la\(\omega_{\text{burn}}\) luz. El perfil de absorción registrado por el detector de esta fuente de luz sonda coincidirá así con el del perfil de línea original, hasta
4. la frecuencia de la fuente de luz de la sonda coincide\(\omega_{\text{burn}}\), sobre lo cual no se registrará ninguna absorción de los fotones de la fuente sonda porque las moléculas que absorben en este régimen de frecuencia han tenido su transición saturada.
5. Por lo tanto, aparecerá un "agujero" en el espectro registrado por el detector de la fuente de luz de la sonda en la región de\(\omega_{\text{burn}}\).

Desafortunadamente, la técnica de la quema de agujeros no proporciona un método completamente confiable para identificar líneas no homogéneamente ensanchadas. Si se observa un agujero en tal experimento de quema, esto proporciona una amplia evidencia, pero si no se ve uno, el resultado no es definitivo. En este último caso, la transición puede no ser lo suficientemente fuerte (es decir, puede no tener una “tasa de absorción de fotones” suficientemente grande) para que la fuente de luz intensa sature la transición en la medida necesaria para formar un agujero.

Esto completa nuestra introducción al tema de la espectroscopia molecular. Tratamientos más avanzados de muchos de los temas tratados aquí, así como muchos aspectos de la espectroscopia experimental moderna, se pueden encontrar en el texto de Zare sobre el momento angular así como en el texto Moléculas y radiación de Steinfeld, 2\(^{nd}\) Edición, de J. I. Steinfeld, MIT Press (1985).

Colaboradores y Atribuciones

• Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry and  Jeff A. Nichols (Oak Ridge National Laboratory)