15.3: Transiciones Electrónica-Vibración-Rotación

El dipolo electrónico de transición y el uso de la simetría de grupo puntual

Volviendo a la expresión

\[ R_{i,f} = \left( \dfrac{2\pi}{\hbar^2} \right) g(\omega_{f,i}) |\textbf{E}_0\cdot{\langle}\phi_f |\mu | \phi_i \rangle |^2 \]

para la tasa de absorción de fotones, nos damos cuenta de que la integral electrónica ahora implica

\[ \langle \psi_{ef} | \mu | \psi_{ei} \rangle = \mu_{f,i} (\textbf{R}), \]

un elemento de matriz de dipolo de transición entre las funciones de onda\(\phi_{e,f}\) electrónicas inicial\(\phi_{e,i}\) y final. Este elemento es una función de las coordenadas vibracionales internas de la molécula, y de nuevo es un vector bloqueado al marco del eje interno de la molécula.

La simetría molecular de grupos de puntos a menudo se puede usar para determinar si un elemento de matriz dipolar de una transición particular desaparecerá y, como resultado, la transición electrónica será “prohibida” y, por lo tanto, predicha que tenga intensidad cero. Si el producto directo de las simetrías de los estados electrónicos inicial y final\(\psi_{ei} \text{ and } \psi_{ef}\) no coincide con la simetría del operador dipolo eléctrico (que tiene la simetría de sus componentes x, y, y z; estas simetrías pueden leerse en la columna más a la derecha de las tablas de caracteres que figuran en el Apéndice E), el elemento de matriz se desvanecerá.

Por ejemplo, la molécula de formaldehído\(H_2CO\) tiene un estado electrónico básico (ver Capítulo 11) que tiene\(^1\text{A}_1\) simetría en el estado excitado\(\text{C}_{2v} \text{point group. Its } \pi \rightarrow \pi^{\text{*}}\) singlete también tiene\(^1\text{A}_1\) simetría porque ambos\(\pi \text{ and } \pi^{\text{*}}\) orbitales son de\(b_1\) simetría. En contraste, la\( \rightarrow \pi^{\text{*}} \text{ singlet excited state is of } ^1\text{A}_2\) simetría n más baja debido a que la mayor energía centrada en el oxígeno n orbital es de\(b_2\) simetría y la\(\pi^{\text{*}} \text{ orbital is of } b_1\) simetría, por lo que el determinante de Slater en el que tanto la n como\(\pi^{\text{*}}\) los orbitales están ocupados individualmente tiene su simetría dictada por la\(b_2 x b_1 \text{ direct product, which is A}_2.\)

La\(\pi \rightarrow \pi^{\text{*}}\) transición implica así estados tierra (\(^1\text{A}_1\)) y excitados (\(^1\text{A}_1\)) cuyo producto directo (\(A_1 \text{ x } A_1) \text{ is of A}_1\)simetría. Por lo tanto, esta transición requiere que el operador de dipolo eléctrico posea un componente de la tabla de caracteres del grupo de\(\text{A}_1 \text{ symmetry. A glance at the C}_{2v}\) puntos que muestra que el eje z molecular es de\(\text{A}_1\) simetría. Por lo tanto, si el campo eléctrico de la luz tiene un componente distinto de cero a lo largo del eje de\(\text{C}_2\) simetría (el eje z de la molécula), se predice que se permitirá la\(\pi \rightarrow \pi^{\text{*}}\) transición. La luz polarizada a lo largo de cualquiera de los otros dos ejes de la molécula no puede inducir esta transición.

En contraste, la\(\rightarrow \pi^{\text{*}}\) transición n tiene un estado excitado por el suelo producto directo de la\(\text{B}_2 \text{ x B}_1 = \text{ A}_2\) simetría. La tabla de caracteres\(\text{C}_{2v}\) del grupo de puntos muestra claramente que el operador dipolo eléctrico (es decir, sus componentes x, y y z en el marco de moléculas fijas) no tiene componente de\(\text{A}_2\) simetría; por lo tanto, la luz sin orientación de campo eléctrico puede inducir esta\(\rightarrow \pi^{\text{*}}\) transición n. Decimos así que la\(\rightarrow \pi^{\text{*}}\) transición n es E1 prohibida (aunque está permitida M1).

Más allá de dicho análisis electrónico de simetría, también es posible derivar reglas de selección vibracional y rotacional para transiciones electrónicas permitidas por E1. Como se hizo en el caso de la espectroscopia vibracional, es convencional expandirse\(\mu_{f,i} (\textbf{R})\) en una serie de potencias sobre la geometría de equilibrio del estado electrónico inicial (ya que esta geometría es más característica de la estructura molecular anterior a la absorción de fotones):

\[ \mu_{f,i}(\textbf{R}) = \mu_{f,i}(\textbf{R}_e) + \sum\limits_a \dfrac{\partial \mu_{f,i}}{\partial R_a} (R_a - R_{a,e}) + .... \]

Los factores Franck-Condon

El primer término en esta expansión, cuando se sustituye en la integral sobre las coordenadas vibracionales, da\(\mu_{f,i}(\textbf{R}_e)\langle \chi_{vf} | \chi_{vi} \rangle \), que tiene la forma del dipolo de transición electrónico multiplicado por la “integral de superposición” entre las funciones de onda vibracionales inicial y final. El\(\mu_{f,i}(\textbf{R}_e)\) factor se discutió anteriormente; es la integral de transición E1 electrónica evaluada en la geometría de equilibrio del estado absorbente. La simetría a menudo se puede utilizar para determinar si esta integral desaparece, como resultado de lo cual la transición E1 quedará “prohibida”.

A diferencia del caso vibración-rotación, las integrales de superposición vibracional\( \langle \chi_{vf} | \chi_{vi} \rangle \) no necesariamente desaparecen porque ya no\(\chi_{vf} \text{ and } \chi_{vi}\) son funciones propias del mismo hamiltoniano vibracional. \(\chi_{vf}\)es una función propia cuya energía potencial es la superficie de energía del estado electrónico final;\(\chi_{vi}\) tiene como potencial la superficie de energía del estado electrónico inicial. Los cuadrados de estas\( \langle \chi_{vf} | \chi_{vi} \rangle \) integrales, que son los que finalmente entran en la expresión de la tasa de transición\( R_{i,f} = \left( \dfrac{2\pi}{\hbar^2} \right) g( \omega_{f,i}) | \textbf{E}_0 \cdot{\langle}\phi_f | \mu | \phi_i \rangle |^2,\) se denominan "factores Franck-Condon”. Sus magnitudes relativas juegan un papel importante en la determinación de las intensidades relativas de varias “bandas” vibracionales (es decir, picos) dentro del espectro de una transición electrónica particular.

Siempre que una transición electrónica provoca un gran cambio en la geometría (longitudes de enlace o ángulos) de la molécula, los factores Franck-Condon tienden a mostrar la característica “progresión amplia” que se muestra a continuación cuando se considera para un nivel vibratorio vi de estado inicial y varios niveles vibracionales de estado final vf:

Figura 15.3.1: ¡Inserta el subtítulo aquí!

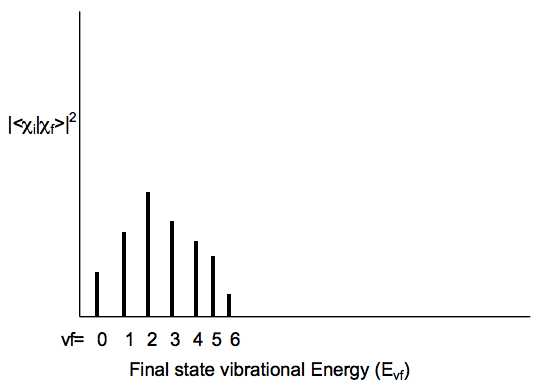
Observe que a medida que uno se mueve hacia valores de vf más altos,\((\text{E}_{vf} - \text{E}_{vf-1})\) disminuye el espaciamiento de energía entre los estados; esto, por supuesto, refleja la anarmonicidad en el potencial vibratorio del estado excitado. Para el ejemplo anterior, la transición al estado vf = 2 tiene el mayor factor FranckCondon. Esto significa que la superposición de la función de\(\chi_{vi} \text{ is largest for the final state's } \chi_{vf}\) función de onda vibratoria del estado inicial con vf = 2.

Como regla cualitativa, cuanto mayor sea la diferencia de geometría entre los potenciales de estado inicial y final, más amplio será el perfil de Franck-Condon (como se muestra arriba) y mayor será el valor de vf para el cual este perfil alcanza su punto máximo. Las diferencias en las frecuencias armónicas entre los dos estados también pueden ampliar el perfil Franck-Condon, aunque no tan significativamente como lo hacen las diferencias geométricas.

Por ejemplo, si los estados inicial y final tienen geometrías y frecuencias muy similares a lo largo del modo que se excita cuando se realiza la excitación electrónica particular, puede resultar el siguiente tipo de perfil Franck-Condon:

Figura 15.3.2: ¡Inserta el subtítulo aquí!

Por el contrario, si los estados electrónicos inicial y final tienen geometrías y/o frecuencias vibracionales muy diferentes a lo largo de algún modo, una envolvente Franck-Condon muy amplia que alcanzó su punto máximo en vf alta resultará como se muestra a continuación:

Figura 15.3.3: ¡Inserta el subtítulo aquí!

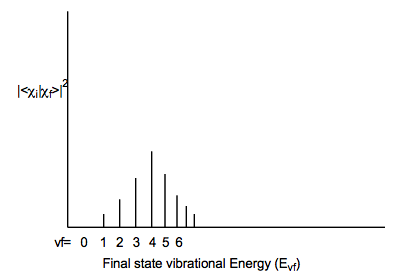
Efectos Vibrónicos

El segundo término en la expansión anterior del elemento de matriz dipolar de transición\( \sum\limits_a \dfrac{\partial \mu_{f,i}}{\partial R_a}(R_a - R_{a,e}) \) puede llegar a ser importante para analizar cuándo\( \mu_{f,i}(\textbf{R}_e) \) desaparece el primer término (por ejemplo, por razones de simetría). Este término derivado dipolo, cuando se sustituye en la integral sobre coordenadas vibracionales da\( \sum\limits_a \dfrac{\partial \mu_{f,i}}{\partial R_a} \langle \chi_{vf} | (R_a - R_{a,e}) | \chi_{vi} \rangle \). Se dice que las transiciones para las que se\(\mu_{f,i}(\textbf{R}_e)\) desvanece pero para las que\( \dfrac{\partial \mu_{f,i}}{\partial R_a} \) no para el modo\(\text{a}^{th}\) vibracional derivan intensidad a través del “acoplamiento vibrónico” con ese modo. Las intensidades de tales modos dependen de cuán fuertemente varía la integral del dipolo electrónico a lo largo del modo (es decir, encendido\(\dfrac{\partial \mu_{f,i}}{\partial \textbf{R}_a}\)) así como de la magnitud de la integral vibracional\( \langle \chi_{vf} | ( R_a - R_{a,e}) | \chi_{vi} \rangle .\)

Un ejemplo de una transición E1 prohibida pero “vibrónicamente permitida” es proporcionada por la transición singlete n\(\rightarrow \pi^{\text{*}}\) de la\(H_2CO\) que se discutió anteriormente en esta sección. Como se detalla allí, el estado electrónico básico tiene\(^1\text{A}_1\) simetría, y la\(\rightarrow \pi^{\text{*}} \text{ state is of } ^1\text{A}_2\) simetría n, por lo que la integral de transición E1\( \langle \psi_{ef} | \mu | \psi_{ei} \rangle \) desaparece para los tres componentes (x, y, z) del operador dipolo eléctrico\(\mu\). Sin embargo, las vibraciones que son de\(\text{b}_2\) simetría (por ejemplo, la vibración de estiramiento asimétrico H-C-H) pueden inducir intensidad en la\(\rightarrow \pi^{\text{*}}\) transición n de la siguiente manera: (i) Para tales vibraciones, la integral vibrónica del\(\text{b}_2\) modo vi = 0 a vf = 1\( \langle \chi_{vf} | (R_a - R_{a,e}) | \chi_{vi} \rangle \) será distinta de cero y probablemente bastante sustancial ( porque, para las funciones del oscilador armónico estas integrales de transición “fundamentales” son dominantes- ver anteriormente); (ii) A lo largo de estos mismos\(\text{b}_2\) modos, la derivada integral dipolo de transición electrónica\( \frac{\partial \mu_{f,i}}{\partial R_a} \) será distinta de cero, aunque la propia integral se\(\mu_{f,i} (\textbf{R}_e)\) desvanezca cuando evaluado en la geometría de equilibrio del estado inicial.

Para entender por qué la derivada\( \frac{\partial \mu_{f,i}}{\partial R_a}\) puede ser distinta de cero para distorsiones (denotada\(R_a) \text{ of b}_2\) simetría, considere esta cantidad con mayor detalle:

\[ \dfrac{\partial \mu_{f,i}}{\partial R_a} = \dfrac{\partial}{\partial R} \langle \psi_{ef} | \mu | \psi_{ei} \rangle = \langle \dfrac{\partial \psi_{ef}}{\partial R_a} | \mu | \psi_{ei} \rangle + \langle \psi_{ef} | \mu | \dfrac{\partial \psi_{ei}}{\partial R_a} \rangle + \langle \psi_{ef} | \dfrac{\partial \mu}{\partial R_a} | \psi_{ei} \rangle . \]

La tercera integral desaparece porque la derivada del propio operador dipolo\( \mu = \sum\limits_i e r_j + \sum\limits_a Z_a e \text{R}_a\) con respecto a las coordenadas de los centros atómicos, produce un operador que contiene solo una suma de cantidades escalares (la carga elemental e y las magnitudes de diversas cargas atómicas\(\text{Z}_a\)); como resultado y debido a que la integral sobre las funciones de onda electrónica se\( \langle \psi+{ef} | \psi_{ei} \rangle \) desvanece, esta contribución rinde cero. La primera y segunda integrales no necesitan desaparecer por simetría porque las derivadas de función de onda\( \frac{\partial \psi_{ef}}{\partial R_a} \text{ and} \frac{\partial \psi_{ei}}{\partial R_a} \) no poseen la misma simetría que sus respectivas funciones de onda.\(\psi_{ef} \text{ and } \psi_{ei}.\) De hecho, se puede demostrar que la simetría de dicha derivada viene dada por el producto directo de las simetrías de su función de onda y la simetría del modo vibratorio que da lugar al\(\frac{\partial }{\partial R_a}. \text{ For the }H_2CO\) caso en cuestión, la vibración de\(\text{b}_2\) modo puede inducir en el\(^1\text{A}_2\) estado excitado un componente derivado (i.e.,\( \frac{\partial \psi_{ef}}{\partial R_a} \)) que es de\(^1\text{B}_1\) simetría) y esta misma vibración puede inducir en el \(^1\text{A}_1\)estado fundamental un componente derivado de\(^1\text{B}_2\) simetría.

Como resultado, se puede esperar que la contribución\( \langle \frac{\psi_{ef}}{\partial R_a} | \mu | \psi_{ei} \rangle \) a\( \frac{\partial \mu_{f,i}}{\partial R_a} \) surgir del acoplamiento vibrónico dentro del estado electrónico excitado sea distinta de cero para los componentes del operador dipolo\(\mu\) que son de\( ( \frac{\partial \psi_{ef}}{\partial R_a} x \psi_{ei}) = (\text{B}_1 \text{ x A}_1) = \text{ B}_1 \) simetría. La luz polarizada a lo largo del eje x de la molécula da tal\(\text{b}_1\) componente a\(\mu\) (ver la tabla de\(\text{C}_{2v}\) caracteres en el Apéndice E). La segunda contribución\( \langle \psi_{ef} | \mu | \frac{\partial \psi_{ei}}{\partial R_a} \rangle \) puede ser distinta de cero para componentes de\(\mu\) que son de\( ( \psi+{ef} \text{ x }\frac{\partial \psi_{ei}}{\partial R_a}) \) =\( ( \text{A}_2 \text{ x B}_2 ) = \text{B}_1 \) simetría; nuevamente, la luz de polarización del eje x puede inducir tal transición.

En resumen, las transiciones electrónicas que son E1 prohibidas por la simetría pueden derivar una intensidad significativa (por ejemplo, en\(H_2CO\) el singlete n la\(\rightarrow \pi^{\text{*}}\) transición es bastante intensa) a través del acoplamiento vibrónico. En dicho acoplamiento, una o más vibraciones (ya sea en el estado inicial o en el final) hacen que la función de onda electrónica respectiva adquiera (a través\( \frac{\partial \psi}{\partial R_a} \)) un componente de simetría que es diferente al de\(\psi\) sí mismo. La simetría de\( \frac{\partial \psi}{\partial R_a} \), que se da como el producto directo de la simetría de\(\psi\) y la de la vibración, puede entonces hacer que la integral\( \langle \psi ' | \mu | \frac{\partial \psi}{\partial R_a} \rangle\) del dipolo eléctrico sea distinta de cero incluso cuando\( \langle \psi ' | \mu | \psi \rangle \) es cero. Se dice que tales transiciones vibrónicamente permitidas derivan su intensidad a través del préstamo vibrónico.

Reglas de selección rotacional para transiciones electrónicas

Cada pico vibracional dentro de una transición electrónica también puede mostrar la estructura rotacional (dependiendo del espaciamiento de las líneas rotacionales, la resolución del espectrómetro y la presencia o ausencia de efectos sustanciales de ensanchamiento de líneas como los discutidos más adelante en este Capítulo). Las reglas de selección para tales transiciones se derivan de una manera que es paralela a la dada anteriormente para el caso de vibración-rotación. La principal diferencia entre esta caja electrónica y la situación anterior es que el momento dipolar de transición vibracional\(\mu_{\text{trans}}\) apropiado al primero es reemplazado por\(\mu_{f,i}(\textbf{R}_e)\) para transiciones convencionales (es decir, no vibrónicas) o\( \frac{\partial \mu_{f,i}}{\partial R_a} \) (para transiciones vibrónicas).

Como antes, cuando\(\mu_{f,i}(\textbf{R}_e) \text{( or } \frac{\partial \mu_{f,i}}{\partial \textbf{R}_a})\) se encuentra a lo largo del eje molecular de una molécula lineal, se denota la transición\(\sigma\) y k = 0 aplica; cuando este vector se encuentra perpendicular al eje se le llama\(\pi\) y k = ±1 pertenece. Las reglas de selección rotacional de moléculas lineales resultantes son las mismas que en el caso de vibración-rotación:

\[ \Delta L = \pm 1, \text{ and } \Delta M = \pm 1,0 \text{ (for } \sigma \text{ transitions).} \]

\[ \Delta L = \pm 1, \text{ and } \Delta M = \pm 1,0 \text{ (for } \pi \text{ transitions).} \]

En este último caso, la situación L = L' = 0 no surge porque una transición p tiene una unidad de momento angular a lo largo del eje molecular lo que imposibilitaría la desaparición tanto de L como de L'.

\[ \Delta L = \pm 1,0; \Delta M = \pm 1,0; \text{ and } \Delta K = 0 \text{ (L = L' = 0 is not allowed and all } \Delta L = 0 \text{ are forbidden when K = K' = 0) } \]

que se aplica cuando\( \mu_{f,i}(\textbf{R}_e) \text{ or } \frac{\partial \mu_{f,i}}{\partial R_a}\) se encuentra a lo largo del eje de simertería, y

\[ \Delta L = \pm 1,0; \Delta M = \pm 1,0; \text{ and } \Delta K = \pm 1 \text{ (L = L' = 0 is not allowed)} \]

que se aplica cuando\(\mu_{f,i}(\textbf{R}_e) \text{ or } \frac{\partial \mu_{f,i}}{\partial R_a}\) se encuentra perpendicular al eje de simetría.

Colaboradores y Atribuciones

• Jack Simons (Henry Eyring Scientist and Professor of Chemistry, U. Utah) Telluride Schools on Theoretical Chemistry and  Jeff A. Nichols (Oak Ridge National Laboratory)