1.5: Combinar operaciones de simetría - 'Multiplicación de Gru
- Page ID
- 69814
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Ahora investigaremos qué sucede cuando aplicamos dos operaciones de simetría en secuencia. Como ejemplo, considere la\(NH_3\) molécula, que pertenece al grupo\(C_{3v}\) puntual. Considera lo que sucede si aplicamos una\(C_3\) rotación seguida de una \(\sigma_v\)reflexión. Escribimos esta operación combinada \(\sigma_v\)\(C_3\)(cuando se escribe, las operaciones de simetría operan sobre la cosa directamente a su derecha, tal como lo hacen los operadores en mecánica cuántica; por lo tanto, tenemos que trabajar hacia atrás de derecha a izquierda desde la notación para obtener el orden correcto en el que el se aplican operadores). Como veremos pronto, es importante el orden en que se aplican las operaciones.
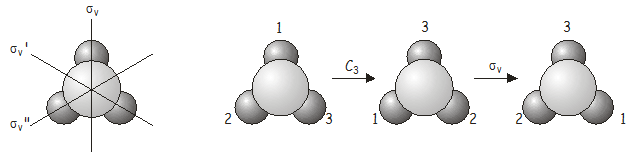
La operación combinada \(\sigma_v\)\(C_3\)es equivalente a \(\sigma_v''\), que también es una operación de simetría del grupo de\(C_{3v}\) puntos. Ahora veamos qué pasa si aplicamos los operadores en el orden inverso es decir\(C_3\)\(\sigma_v\) (\(\sigma_v\)seguido de \(C_3\)).
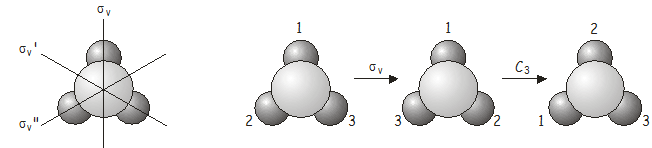
Nuevamente, la operación combinada\(C_3\)\(\sigma_v\) equivale a otra operación del grupo de puntos, esta vez \(\sigma_v'\).
Hay dos puntos importantes que se ilustran con este ejemplo:
- El orden en que se aplican dos operaciones es importante. Para dos operaciones de simetría\(A\) y\(B\), no\(AB\) es necesariamente lo mismo que\(BA\), es decir, las operaciones de simetría no se conmutan en general. En algunos grupos los elementos de simetría sí viajan; se dice que tales grupos son abelianos.
- Si dos operaciones del mismo grupo de puntos se aplican en secuencia, el resultado será equivalente a otra operación del grupo de puntos. Se dice que las operaciones de simetría que están relacionadas entre sí por otras operaciones de simetría del grupo pertenecen al mismo culo cl. En\(NH_3\), los tres planos de espejo \(\sigma_v\), \(\sigma_v'\)y \(\sigma_v''\)pertenecen a la misma clase (relacionados entre sí a través de una\(C_3\) rotación), al igual que las rotaciones\(C_3^+\) y\(C_3^-\) ( rotaciones en sentido antihorario y en el sentido de las agujas del reloj alrededor del eje principal, relacionadas entre sí por un plano de espejo vertical
Los efectos de aplicar dos operaciones de simetría en secuencia dentro de un grupo de puntos dado se resumen en tablas de multiplicación gro up. A modo de ejemplo, a continuación se muestra la tabla de multiplicación de grupos completa para\(C_{3v}\) usar las operaciones de simetría definidas en las figuras anteriores. Las operaciones escritas a lo largo de la primera fila de la tabla se realizan primero, seguidas de las escritas en la primera columna (tenga en cuenta que la tabla cambiaría si optamos por nombrar \(\sigma_v\), \(\sigma_v'\)y \(\sigma_v''\)en algún orden diferente).
\[\begin{array}{l|llllll} C_{3v} & E & C_3^+ & C_3^- & \sigma_v & \sigma_v' & \sigma_v'' \\ \hline E & E & C_3^+ & C_3^- & \sigma_v & \sigma_v' & \sigma_v'' \\ C_3^+ & C_3^+ & C_3^- & E & \sigma_v' & \sigma_v'' & \sigma_v \\ C_3^- & C_3^- & E & C_3^+ & \sigma_v'' & \sigma_v & \sigma_v' \\ \sigma_v & \sigma_v & \sigma_v'' & \sigma_v' & E & C_3^- & C_3^+ \\ \sigma_v' & \sigma_v' & \sigma_v & \sigma_v'' & C_3^+ & E & C_3^- \\ \sigma_v'' & \sigma_v'' & \sigma_v' & \sigma_v & C_3^- & C_3^+ & E \end{array} \label{5.1}\]

