3.5: Gráficos de Barras e Histogramas
- Page ID
- 73907
Dado que una distribución discreta está completamente especificada por las probabilidades de cada uno de sus eventos, podemos representarla mediante un gráfico de barras. La probabilidad de cada evento está representada por la altura de una barra. Podemos generalizar esta representación gráfica para representar distribuciones continuas. Para ver lo que tenemos en mente, consideremos un ejemplo particular.
Supongamos que tenemos una pistola radar y que decidimos interesarnos por las velocidades típicas de los autos en una autopista a las afueras de la ciudad. Al pensar en este proyecto, reconocemos que las velocidades pueden variar con la hora del día y el día de la semana. Las variaciones aleatorias en muchos otros factores también pueden ser importantes; estos incluyen las condiciones climáticas y los accidentes en las cercanías. Para eliminar tantos factores atípicos como sea posible, podríamos decidir que las velocidades típicas son las de los autos que van hacia el norte entre la 1:00pm y las 4:00pm de lunes a viernes cuando la superficie de la carretera está seca y no hay vehículos discapacitados a la vista. Si tenemos mucho tiempo y la carretera está ocupada, podríamos recopilar muchos datos. Supongamos que registramos las velocidades de los\(10,000\) autos. Cada dato sería la velocidad de un automóvil en la carretera en un momento en que se cumplen las condiciones seleccionadas.
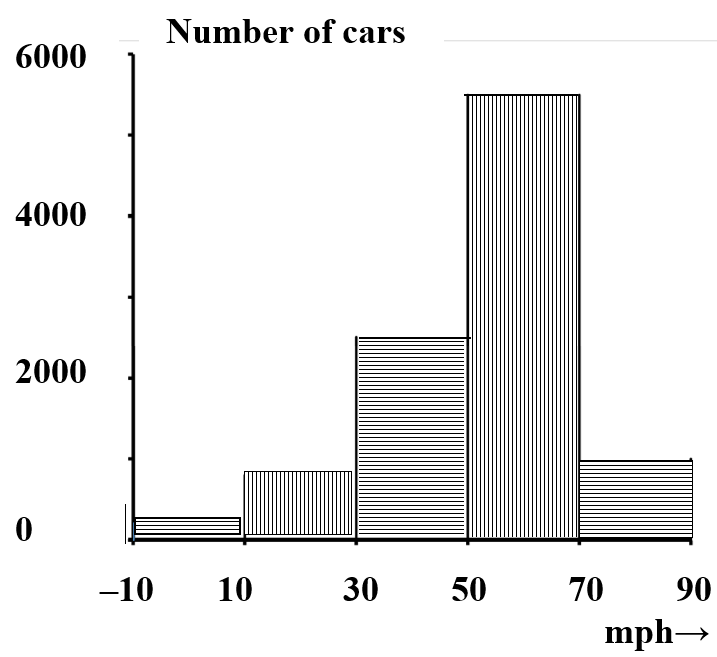
Para utilizar estos datos, queremos resumirlos en una forma que sea fácil de visualizar. Una forma de hacerlo es agregar los datos para dar el número de autos en cada rango de\(20\) mph; los resultados podrían parecerse a los datos del Cuadro 2. La Figura 3 es un gráfico de barras de cinco canales que muestra el número de autos en cada rango de\(20\) mph. Una gran cantidad de información se pierde en el proceso de agregación. En particular, nada en la gráfica representa el número de automóviles en intervalos de velocidad más estrechos.
| Velocidad (mph) | Número de autos | Fracción de autos | Altura para que el área de barra sea igual a fracción |
|---|---|---|---|
| —10 | |||
| 200 | 0.020 | 0.20/20 = 0.0010 | |
| 10 | |||
| 800 | 0.08 | 0.08/20 = 0.0040 | |
| 30 | |||
| 2500 | 0.25 | 0.25/20 = 0.0125 | |
| 50 | |||
| 5500 | 0.55 | 0.55/20 = 0.0275 | |
| 70 | |||
| 1000 | 0.10 | 0.10/20 = 0.0050 | |
| 90 |
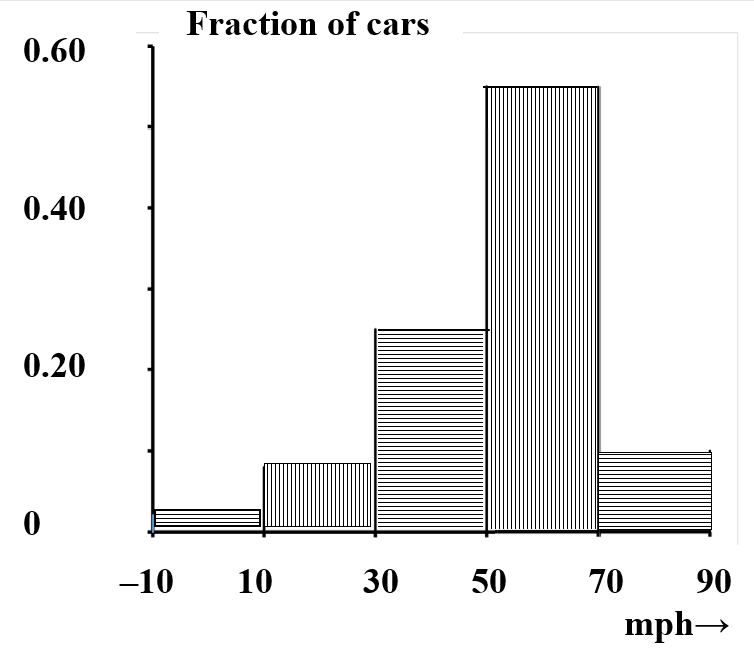
Ahora, supongamos que repetimos esta tarea, pero que no tenemos tiempo suficiente para recabar datos sobre tantos como\(10,000\) más autos. Tendremos curiosidad por la medida en que nuestras dos muestras coinciden entre sí. Dado que el número total de vehículos será diferente, la forma apropiada de hacerlo es obviamente comparar la fracción de autos en cada rango de velocidad. De hecho, el uso de fracciones nos permite comparar cualquier número de tales estudios. En la medida en que estos estudios midan lo mismo, velocidades típicas en las condiciones especificadas, la fracción de automóviles en cualquier intervalo de velocidad particular debe ser aproximadamente constante. Dividir el número de automóviles en cada intervalo de velocidad por el número total de automóviles da una representación que enfoca la atención en la proporción de automóviles con diversas velocidades. La forma de la gráfica de barras sigue siendo la misma; todo lo que cambia es la escala que usamos para etiquetar la ordenada. (Ver Figura 4.)
En la medida en que cualquier repetición de este experimento da casi los mismos resultados, este es un cambio útil. Sin embargo, las limitaciones fundamentales de la gráfica permanecen. Por ejemplo, si queremos usar la gráfica para estimar cómo se distribuyen las velocidades en cualquier otro conjunto de intervalos, tenemos que leer valores fuera de la ordenada y manipularlos de formas que pueden no ser muy satisfactorias. Para estimar la fracción con velocidades entre\(20\) mph y\(40\) mph, podríamos asignar la mitad de los automóviles en el intervalo\(10-30\) mph y la mitad de los del intervalo\(30-50\) mph al nuevo intervalo. Esto nos permite estimar que la fracción en el intervalo\(20-40\) mph es\(0.165\). Esta estimación es mucho menos confiable que una que podría hacerse volviendo a los datos brutos para todos los\(10,000\) automóviles.
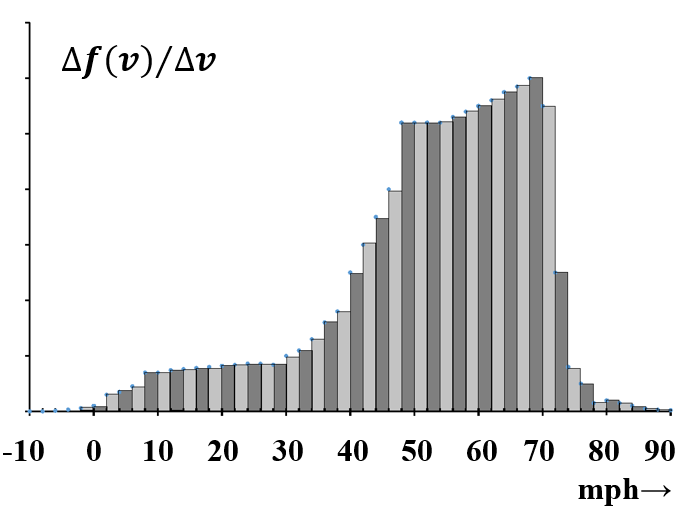
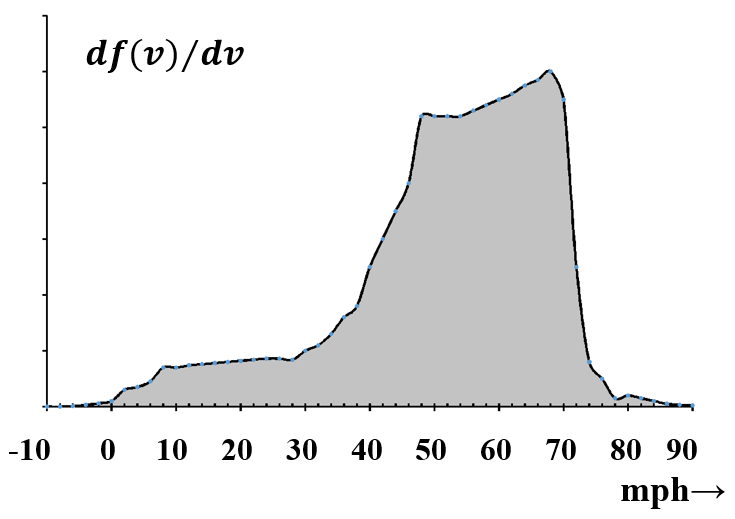
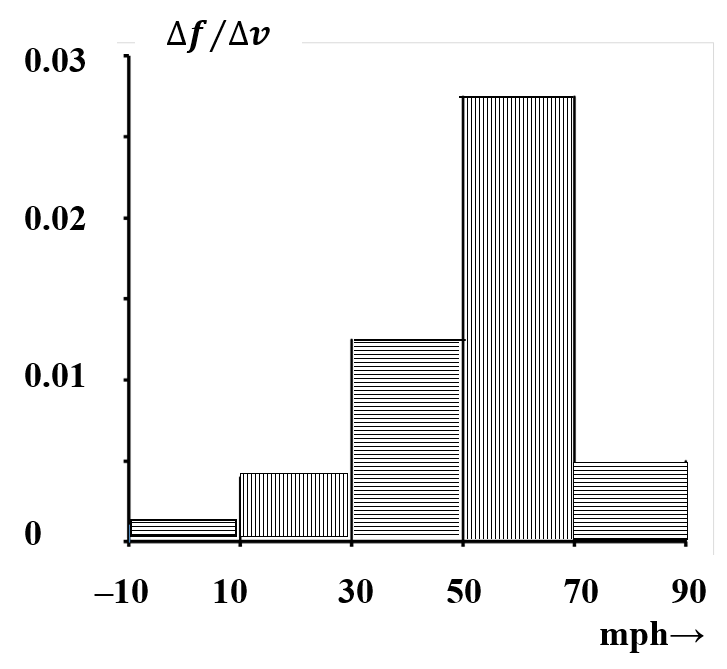
Los datos también se pueden representar como un histograma. En un histograma, la información está representada por el área en lugar de la altura de la barra. En el presente caso, el único cambio visible en la gráfica es otro cambio en los valores numéricos en la ordenada. En la Figura 5, el área de una barra representa la fracción de automóviles con velocidades en el intervalo dado. A medida que el intervalo de velocidad se hace más pequeño, cualquiera de estos gráficos de barras se parece cada vez más a una curva continua. (Ver Figura 6.) El histograma tiene la ventaja de que, a medida que la curva se vuelve continua, la interpretación permanece constante: el área bajo la curva entre dos velocidades cualesquiera siempre representa la fracción de automóviles con velocidades en este intervalo. Resulta que somos adeptos a estimar visualmente las áreas relativas de diferentes partes de un histograma. Es decir, de un rápido vistazo a un histograma, podemos obtener una buena apreciación semicuantitativa de la importancia de los datos subyacentes.
Si el histograma captura nuestra experiencia, y esperamos que los eventos futuros tengan las mismas características, el histograma se convierte en una expresión de probabilidad. Todo lo que es necesario es que construyamos el histograma para que el área total debajo de la gráfica sea la unidad. Si dejamos\(f\left(u\right)\) ser el área debajo de la gráfica de\(u=-\infty \) a\(u=u\), entonces\(f\left(u\right)\) representa la probabilidad de que la velocidad de un automóvil seleccionado al azar se encuentre entre\(-\infty\) y\(u\). Para cualquiera\(a\) y b, la probabilidad que\(u\) se encuentra en el intervalo\(a<b\) > es\(f\left(b\right)-f\left(a\right)\). A la función\(f\left(u\right)\) se le llama la función de distribución de probabilidad acumulativa, porque su valor para cualquiera\(u\) es la fracción de automóviles que tienen una velocidad menor que\(u\). \(f\left(a\right)\)es la frecuencia con la que observamos valores de la variable aleatoria,\(u\), que son menores que\(a\). Equivalentemente, podemos decir que\(f\left(u\right)\) es la probabilidad de que cualquier automóvil seleccionado al azar tenga una velocidad menor que\(u\). Si dejamos que el ancho de cada intervalo vaya a cero, la representación gráfica de barras del histograma se convierte en una curva, y el histograma se convierte en una función continua de la variable aleatoria,\(u\). (Ver Figura 7.) Obsérvese que la curva —la envolvente envolvente— no lo es\(\boldsymbol{f}\left(\boldsymbol{u}\right)\) . \(\boldsymbol{\ \ }\boldsymbol{f}\left(\boldsymbol{u}\right)\)es el área bajo la curva envolvente envolvente.