3.8: Una visión heurística de la función de distribución acumulativa

Podemos usar estas ideas para crear una gráfica que se aproxime a la función de distribución de probabilidad acumulativa dado cualquier conjunto de\(N\) mediciones de una variable aleatoria\(u\). Para ello, ponemos los\(u_i\) valores que se encuentran en nuestras\(N\) medidas en orden de menor a mayor. Etiquetamos los valores ordenados\(u_1\),\(u_2\),...,\(u_i\),...\(u_N\), donde\(u_1\) está el más pequeño. Por el argumento que desarrollamos en el apartado anterior, la probabilidad de observar un valor menor que\(u_1\) se trata\({1}/{\left(N+1\right)}\). Si tuviéramos que hacer un gran número de mediciones adicionales, una fracción de aproximadamente\({1}/{\left(N+1\right)}\) de este gran número de mediciones adicionales sería menor que\(u_1\). Esta fracción es justa\(f\left(u_1\right)\), así que razonamos eso\(f\left(u_1\right)\approx {1}/{\left(N+1\right)}\). La probabilidad de observar un valor entre\(u_1\) y también\(u_2\) es sobre\({1}/{\left(N+1\right)}\); así la probabilidad de observar un valor menor que\(u_2\) es aproximadamente\({2}/{\left(N+1\right)}\), y esperamos\(f\left(u_2\right)\approx {2}/{\left(N+1\right)}\). En general, la probabilidad de observar un valor entre\(u_{i-1}\) y también\(u_i\) es aproximadamente\({1}/{\left(N+1\right)}\), y la probabilidad de observar un valor menor que\(u_i\) es aproximadamente\({i}/{\left(N+1\right)}\). En otras palabras, esperamos que la función de distribución de probabilidad acumulativa\(u_i\) para sea tal que la observación\(i^{th}\) más pequeña corresponda a\(f\left(u_i\right)\approx {i}/{\left(N+1\right)}\). La cantidad a menudo\({i}/{\left(N+1\right)}\) se denomina probabilidad de rango del punto de\(i^{th}\) datos.

Figura 11. Una función de distribución de probabilidad acumulada aproximada.

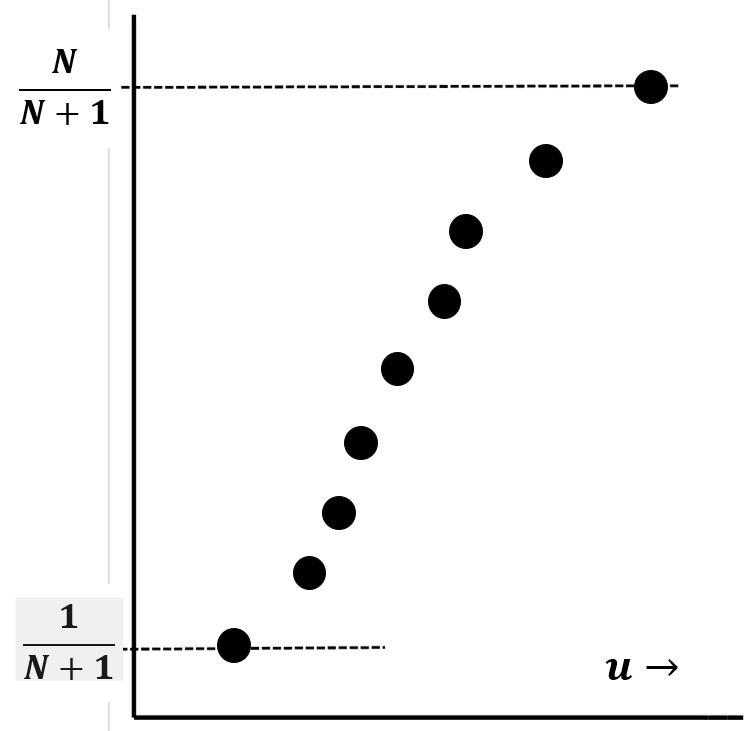
La Figura 11 es un boceto de la forma sigmoidea que normalmente esperamos encontrar cuando trazamos\({i}/{\left(N+1\right)}\) versus el\(i^{th}\) valor de\(u\). Esta gráfica se aproxima a la función de distribución de probabilidad acumulativa,\(f\left(u\right)\). Esperamos la forma sigmoidea porque esperamos que los valores observados de se\(u\) agrupen alrededor de su valor promedio. (Si, dentro de algún dominio de\(u\) valores, todos los valores posibles de\(u\) fueran igualmente probables, esperaríamos que la diferencia entre los sucesivos valores observados de\(u\) sea aproximadamente constante, lo que haría que la gráfica pareciera aproximadamente lineal). En cualquier valor de\(u\), la pendiente de la curva es solo la función probabilidad-densidad,\({df\left(u\right)}/{du}\).

Estas ideas significan que podemos probar si los datos experimentales son descritos por algún modelo matemático en particular, digamos\(F\left(u\right)\). Para ello, utilizamos el modelo matemático para predecir cada uno de los valores de probabilidad de rango N:\({1}/{\left(N+1\right)}\),\({2}/{\left(N+1\right)}\),...,\({i}/{\left(N+1\right)}\),...,\({N}/{\left(N+1\right)}\). Es decir, calculamos\(F\left(u_1\right)\),,...\(F\left(u_2\right)\),\(F\left(u_i\right)\),...,\(F\left(u_N\right)\); si\(F\left(u\right)\) describe bien los datos, encontraremos, para todos\(i\),\(F\left(u_i\right)\approx {i}/{\left(N+1\right)}\). Gráficamente, podemos probar la validez de la relación trazando\({i}/{\left(N+1\right)}\) versus\(F\left(u_i\right)\). Si\(F\left(u\right)\) describe bien los datos, esta gráfica será aproximadamente lineal, con una pendiente de uno.

En la Sección 3.12, se introduce la distribución normal, que es un modelo matemático que describe muchas fuentes de observaciones experimentales. La distribución normal es una función de distribución que involucra dos parámetros, la media\(\mu\), y la desviación estándar,\(\sigma\). Las ideas que hemos discutido pueden ser utilizadas para desarrollar un papel gráfico en particular, generalmente llamado papel de probabilidad normal. Si los datos se distribuyen normalmente, trazarlos en este papel produce una línea aproximadamente recta.

Podemos hacer esencialmente la misma prueba sin beneficio de papel cuadriculado especial, calculando el promedio\(\overline{u}\approx \mu\), y la desviación estándar estimada,\(s\approx \sigma\), a partir de los datos experimentales. (Cálculo\(\overline{u}\) y\(s\) se discute a continuación.) Usando\(\overline{u}\) y\(s\) como estimaciones de\(\mu\) y\(\sigma\), podemos encontrar la probabilidad predicha por el modelo de observar un valor de la variable aleatoria que es menor que\(u_i\). Este valor es\(f\left(u_i\right)\) para una distribución normal cuya media es\(\overline{u}\) y cuya desviación estándar es\(s\). Podemos encontrar\(f\left(u_i\right)\) usando tablas estándar (generalmente llamadas la curva normal de error en compilaciones matemáticas), integrando numéricamente la función de densidad de probabilidad de la distribución normal, o usando una función incrustada en una hoja de cálculo programa, como Excel\({}^{\circledR }\). Si los datos son descritos por la función de distribución normal, este valor debe ser aproximadamente igual a la probabilidad de rango; es decir, esperamos\(f\left(u_i\right)\approx {i}/{\left(N+1\right)}\). Una parcela de\({i}/{\left(N+1\right)}\) versus\(f\left(u_i\right)\) será aproximadamente lineal con una pendiente de aproximadamente uno.