3.10: Estadística - la media y la varianza de una distribución
- Page ID
- 73920
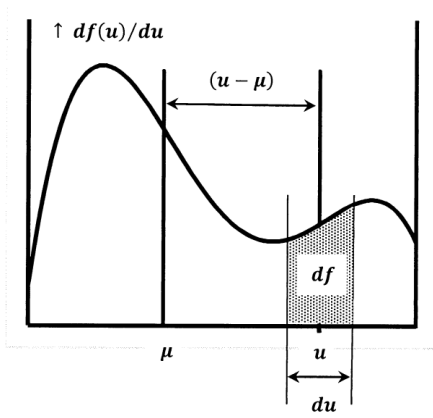
Hay dos estadísticas importantes asociadas a cualquier distribución de probabilidad, la media de una distribución y la varianza de una distribución. La media se define como el valor esperado de la propia variable aleatoria. La letra griega\(\mu\) se suele utilizar para representar la media. Si\(f\left(u\right)\) es la distribución de probabilidad acumulativa, la media es el valor esperado para\(g\left(u\right)=u\). De nuestra definición de valor esperado, la media es
\[\mu =\int^{\infty }_{-\infty }{u\left(\frac{df}{du}\right)du}\]
La varianza se define como el valor esperado de\({\left(u-\mu \right)}^2\). La varianza mide qué tan dispersos están los datos. Si la varianza es grande, los datos están —en promedio— más alejados de la media que si la varianza es pequeña. La desviación estándar es la raíz cuadrada de la varianza. La letra griega\(\sigma\) se suele utilizar para denotar la desviación estándar. Entonces,\(\sigma^2\) denota la varianza, y
\[\sigma^2=\int^{\infty }_{-\infty }{{\left(u-\mu \right)}^2\left(\frac{df}{du}\right)du}\]
Si tenemos un pequeño número de puntos de una distribución, podemos estimar\(\mu\) y\(\sigma\) aproximando estas integrales como sumas sobre el dominio de la variable aleatoria. Para ello, necesitamos estimar la probabilidad asociada a cada intervalo para el cual tenemos un punto de muestreo. Por el argumento que hacemos en la Sección 3.7, la mejor estimación de esta probabilidad es simplemente\({1}/{N}\), donde\(N\) está el número de puntos de muestreo. Por lo tanto, tenemos
\[\mu =\int^{\infty }_{-\infty }{u\left(\frac{df}{du}\right)du\approx \sum^N_1{u_i\left(\frac{1}{N}\right)=\overline{u}}}\]
Es decir, la mejor estimación que podemos hacer de la media a partir de puntos de\(N\) datos es\(\overline{u}\), donde\(\overline{u}\) está la media aritmética ordinaria. Del mismo modo, la mejor estimación que podemos hacer de la varianza es
\[ \sigma^2 = \int_{- \infty}^{ \infty} (u - \mu )^2 \left( \frac{df}{du} \right) du \approx \sum_{i=1}^N (u_i - \mu )^2 \left( \frac{1}{N} \right)\]
Ahora surge una complicación en que normalmente no conocemos el valor de\(\mu\). Lo mejor que podemos hacer es estimar su valor como\(\mu \approx \overline{u}\). Resulta que usando esta aproximación en la ecuación que deducimos para la varianza da una estimación de la varianza que es demasiado pequeña. Un argumento más detallado (ver Sección 3.14) muestra que, si utilizamos\(\overline{u}\) para aproximar la media, la mejor estimación de\(\sigma^2\), generalmente denotada\(s^2\), es
\[estimated\ \sigma^2=s^2=\sum^N_{i=1}{{\left(u_i-\overline{u}\right)}^2\left(\frac{1}{N-1}\right)}\]
Dividir por\(N-1\), en lugar de\(N\), compensa exactamente el error introducido usando\(\overline{u}\) en lugar de\(\mu\).
La media es análoga a un centro de masa. La varianza es análoga a un momento de inercia. Por esta razón, la varianza también se llama el segundo momento sobre la media. Para mostrar estas analogías, imaginemos que dibujamos la función de densidad de probabilidad sobre una placa de acero uniformemente gruesa y luego cortamos a lo largo de la curva y el\(u\) eje -eje (Figura\(\PageIndex{1}\)). Dejar\(M\) ser la masa de la pieza recortada de placa;\(M\) es la masa por debajo de la curva de densidad de probabilidad. Dejar\(dA\) y\(dm\) ser los incrementos de área y masa en la rebanada delgada del recorte que se encuentra por encima de un pequeño incremento,\(du\), de\(u\). Dejar\(\rho\) ser la densidad de la placa, expresada como masa por unidad de área. Dado que la placa es uniforme,\(\rho\) es constante. Tenemos\(dA=\left({df}/{du}\right)du\) y\(dm=\rho dA\) para que
\[dm=\rho \left(\frac{df}{du}\right)du\]
La media de la distribución corresponde a una línea vertical en este recorte en\(u=\mu\). Si el recorte se apoya en un filo de cuchilla a lo largo de la línea\(u=\mu\), la gravedad no induce par; el recorte está equilibrado. Dado que el par es cero, tenemos
\[0=\int^M_{m=0}{\left(u-\mu \right)dm=\int^{\infty }_{-\infty }{\left(u-\mu \right)\rho \left(\frac{df}{du}\right)du}}\]
Dado que\(\mu\) es una propiedad constante del recorte, se deduce que
\[\mu =\int^{\infty }_{-\infty }{u\left(\frac{df}{du}\right)}du\]
El momento de inercia del recorte sobre la línea\(u=\mu\) es
\[\begin{aligned} I & =\int^M_{m=0}{{\left(u-\mu \right)}^2dm} \\ ~ & =\int^{\infty }_{-\infty }{{\left(u-\mu \right)}^2\rho \left(\frac{df}{du}\right)du} \\ ~ & =\rho \sigma^2 \end{aligned}\]
El momento de inercia sobre la línea\(u-\mu\) es simplemente la masa por unidad de área,\(\rho\), multiplicada por la varianza de la distribución. Si lo dejamos\(\rho =1\), tenemos\(I=\sigma^2\).
Definimos la media de\(f\left(u\right)\) como el valor esperado de\(u\). Es el valor de\(u\) que debemos “esperar” obtener la próxima vez que muestremos la distribución. Alternativamente, podemos decir que la media es la mejor predicción que podemos hacer sobre el valor de una muestra futura a partir de la distribución. Si sabemos\(\mu\), la mejor predicción que podemos hacer es\(u_{predicted}=\mu\). Si solo tenemos la media estimada,\(\overline{u}\), entonces\(\overline{u}\) es la mejor predicción que podamos hacer. Elegir\(u_{predicted}=\overline{u}\) marca la diferencia,\(\ \left|u-u_{predicted}\right|\), lo más pequeña posible.
Estas ideas se relacionan con otra interpretación de la media. Vimos que la varianza es el segundo momento sobre la media. El primer momento sobre la media es
\[ \begin{aligned} 1^{st}\ moment & =\int^{\infty }_{-\infty }{\left(u-\mu \right)}\left(\frac{df}{du}\right)du \\ ~ & =\int^{\infty }_{-\infty }{u\left(\frac{df}{du}\right)du}-\mu \int^{\infty }_{-\infty }{\left(\frac{df}{du}\right)du} \\ ~ & =\mu -\mu \\ ~ & =0 \end{aligned}\]
Dado que las dos últimas integrales son\(\mu\) y 1, respectivamente, el primer momento sobre la media es cero. Podríamos haber definido la media como el valor,\(\mu\), para lo cual el primer momento de\(u\) aproximadamente\(\mu\) es cero.
El primer momento sobre la media es cero. El segundo momento sobre la media es la varianza. Podemos definir los momentos tercero, cuarto y superior sobre la media. Algunos de estos momentos superiores tienen aplicaciones útiles.


