4.1: Funciones de distribución para componentes de velocidad de gas
- Page ID
- 74518
En el Capítulo 2, asumimos que todas las moléculas de un gas se mueven con la misma velocidad y utilizamos un argumento simplificado para concluir que esta velocidad depende únicamente de la temperatura. Ahora reconocemos que las moléculas individuales en una muestra de gas tienen un amplio rango de velocidades; las velocidades de las moléculas de gas deben describirse mediante una función de distribución. Es cierto, sin embargo, que la velocidad promedio depende sólo de la temperatura.
James Clerk Maxwell fue el primero en derivar la función de distribución para las velocidades del gas. Lo hizo alrededor de 1860. Seguimos el argumento de Maxwell. Para una molécula que se mueve en tres dimensiones, hay tres componentes de velocidad. El argumento de Maxwell utiliza solo una suposición: la velocidad de una molécula de gas es independiente de la dirección en la que se mueve. Equivalentemente, podemos decir que los componentes de la velocidad de una molécula de gas son independientes entre sí; conocer el valor de un componente de la velocidad de una molécula no nos permite inferir nada sobre los valores de los otros dos componentes. Cuando usamos coordenadas cartesianas, la suposición de Maxwell AssumptionMaxwell significa también que el mismo modelo matemático debe describir la distribución de cada uno de los componentes de velocidad.
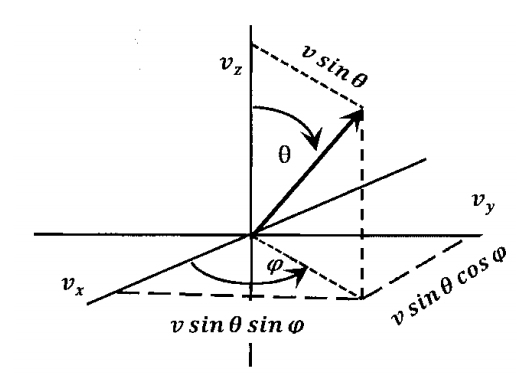
Dado que la velocidad de una molécula de gas tiene tres componentes, debemos tratar la distribución de velocidad como una función de tres variables aleatorias. Para entender cómo se puede hacer esto, consideremos cómo podríamos encontrar funciones de distribución de probabilidad para componentes de velocidad. Debemos considerar sistemas de coordenadas tanto esféricas como cartesianas.
Supongamos que somos capaces de medir los componentes de coordenadas cartesianas\(v_x\)\(v_y\), y\(v_z\) de las velocidades de un gran número de moléculas de gas seleccionadas aleatoriamente en una muestra particular de temperatura constante. Luego podemos transformar cada conjunto de componentes cartesianos en componentes de covelocidad de covelocidad de coordenadas esféricas\(v\),\(\theta\), y\(\varphi\). Imaginamos acumular los resultados de estas mediciones en una tabla como la Tabla 1. Como cuestión práctica, por supuesto, no podemos hacer las medidas para completar tal tabla. Sin embargo, no cabe duda de que, a cada instante, cada molécula de gas puede caracterizarse por un conjunto de tales componentes de velocidad; los valores existen, aunque no podamos medirlos. Imaginamos que tenemos esos datos sólo como una forma de aclarar las propiedades de las funciones de distribución que necesitamos.
Cuadro 1. Componentes de velocidad molecular
| Número de Molécula | \({\boldsymbol{v}}_{\boldsymbol{x}}\) | \({\boldsymbol{v}}_{\boldsymbol{x}}\) | \({\boldsymbol{v}}_{\boldsymbol{x}}\) | v | \(\boldsymbol{\theta }\) | \(\boldsymbol{\varphi }\) |
|---|---|---|---|---|---|---|
| 1 | \ ({\ boldsymbol {v}} _ {\ boldsymbol {x}}\)” style="vertical-align:middle; ">\(v_x\left(1\right)\) | \ ({\ boldsymbol {v}} _ {\ boldsymbol {x}}\)” style="vertical-align:middle; ">\(v_y\left(1\right)\) | \ ({\ boldsymbol {v}} _ {\ boldsymbol {x}}\)” style="vertical-align:middle; ">\(v_z\left(1\right)\) | \(v\left(1\right)\) | \ (\ negridsymbol {\ theta}\)” style="vertical-align:middle; ">\(\theta \left(1\right)\) | \ (\ negridsymbol {\ varphi}\)” style="vertical-align:middle; ">\(\varphi \left(1\right)\) |
| 2 | \ ({\ boldsymbol {v}} _ {\ boldsymbol {x}}\)” style="vertical-align:middle; ">\(v_x\left(2\right)\) | \ ({\ boldsymbol {v}} _ {\ boldsymbol {x}}\)” style="vertical-align:middle; ">\(v_y\left(2\right)\) | \ ({\ boldsymbol {v}} _ {\ boldsymbol {x}}\)” style="vertical-align:middle; ">\(v_z\left(2\right)\) | \(v\left(2\right)\) | \ (\ negridsymbol {\ theta}\)” style="vertical-align:middle; ">\(\theta \left(2\right)\) | \ (\ negridsymbol {\ varphi}\)” style="vertical-align:middle; ">\(\varphi \left(2\right)\) |
| 3 | \ ({\ boldsymbol {v}} _ {\ boldsymbol {x}}\)” style="vertical-align:middle; ">\(v_x\left(3\right)\) | \ ({\ boldsymbol {v}} _ {\ boldsymbol {x}}\)” style="vertical-align:middle; ">\(v_y\left(3\right)\) | \ ({\ boldsymbol {v}} _ {\ boldsymbol {x}}\)” style="vertical-align:middle; ">\(v_z\left(3\right)\) | \(v\left(3\right)\) | \ (\ negridsymbol {\ theta}\)” style="vertical-align:middle; ">\(\theta \left(3\right)\) | \ (\ negridsymbol {\ varphi}\)” style="vertical-align:middle; ">\(\varphi \left(3\right)\) |
| 4 | \ ({\ boldsymbol {v}} _ {\ boldsymbol {x}}\)” style="vertical-align:middle; ">\(v_x\left(4\right)\) | \ ({\ boldsymbol {v}} _ {\ boldsymbol {x}}\)” style="vertical-align:middle; ">\(v_y\left(4\right)\) | \ ({\ boldsymbol {v}} _ {\ boldsymbol {x}}\)” style="vertical-align:middle; ">\(v_z\left(4\right)\) | \(v\left(4\right)\) | \ (\ negridsymbol {\ theta}\)” style="vertical-align:middle; ">\(\theta \left(4\right)\) | \ (\ negridsymbol {\ varphi}\)” style="vertical-align:middle; ">\(\varphi \left(4\right)\) |
| ... | \ ({\ boldsymbol {v}} _ {\ boldsymbol {x}}\)” style="vertical-align:middle; ">... | \ ({\ boldsymbol {v}} _ {\ boldsymbol {x}}\)” style="vertical-align:middle; ">... | \ ({\ boldsymbol {v}} _ {\ boldsymbol {x}}\)” style="vertical-align:middle; ">... | ... | \ (\ negridsymbol {\ theta}\)” style="vertical-align:middle; ">... | \ (\ negridsymbol {\ varphi}\)” style="vertical-align:middle; ">... |
| \(N\) | \ ({\ boldsymbol {v}} _ {\ boldsymbol {x}}\)” style="vertical-align:middle; ">\(v_x\left(N\right)\) | \ ({\ boldsymbol {v}} _ {\ boldsymbol {x}}\)” style="vertical-align:middle; ">\(v_x\left(N\right)\) | \ ({\ boldsymbol {v}} _ {\ boldsymbol {x}}\)” style="vertical-align:middle; ">\(v_z\left(N\right)\) | \(v\left(N\right)\) | \ (\ negridsymbol {\ theta}\)” style="vertical-align:middle; ">\(\theta \left(N\right)\) | \ (\ negridsymbol {\ varphi}\)” style="vertical-align:middle; ">\(\varphi \left(N\right)\) |
Estos datos tienen varias características importantes. La velocidad escalar,\(v\), varía de 0 a\(+\infty\);\(v_x\),\(v_y\), y\(v_z\) van desde\(-\infty\) hasta\(+\infty\). En § 2, vemos que\(\theta\) varía de 0 a\(\pi\); y\(\varphi\) va de 0 a\(2\pi\). Cada columna representa datos muestreados de la distribución de la variable aleatoria correspondiente. En el Capítulo 3, encontramos que podemos usar dichos datos para encontrar modelos matemáticos para tales distribuciones. Aquí, podemos encontrar modelos matemáticos para las funciones de distribución acumulativa\(f_x\left(v_x\right)\),\(f_y\left(v_y\right)\), y\(f_z\left(v_z\right)\). Podemos aproximar la gráfica de\(f_x\left(v_x\right)\) trazando la probabilidad de rango de\(v_x\) versus\(v_x\). Esperamos que esta parcela sea sigmoide; en cualquiera\(v_x\), la pendiente de esta parcela es la función probabilidad-densidad,\({df_x\left(v_x\right)}/{dv_x}\). La función de densidad de probabilidad para\(v_x\) depende únicamente de\(v_x\), porque el valor medido para\(v_x\) es independiente de los valores medidos para\(v_y\) y\(v_z\). Sin embargo, según el supuesto de Maxwell, las funciones que describen la distribución de\(v_y\) y\(v_z\) son las mismas que las que describen la distribución de\(v_x\). Si bien es redundante, es conveniente introducir símbolos adicionales para representar estas funciones de densidad de probabilidad. Definimos\({\rho }_x\left(v_x\right)={df_x\left(v_x\right)}/{dv_x}\),\({\rho }_y\left(v_y\right)={df_y\left(v_y\right)}/{dv_y}\), y\({\rho }_z\left(v_z\right)={df_z\left(v_z\right)}/{dv_z}\).
Cuando encontramos estas funciones de distribución unidimensional modelando los datos experimentales de esta manera, cada\(v_x\) dato que utilizamos en nuestro análisis proviene de una observación sobre una molécula y se asocia con\(v_z\) valores particulares\(v_y\) y. Estos valores de\(v_y\) y\(v_z\) pueden ser cualquier cosa, desde\(-\infty\) hasta\(+\infty\). Este es un punto significativo. Las funciones\(f_x\left(v_x\right)\) y\({df_x\left(v_x\right)}/{dv_x}\) son independientes de\(v_y\) y\(v_z\). También podemos decir que\({df_x\left(v_x\right)}/{dv_x}\) describe la distribución de\(v_x\) cuándo\(v_y\) y\(v_z\) se promedian sobre todos los valores que es posible que tengan.
Para aclarar esto, consideremos otra función de distribución de probabilidad acumulativa\(f_{xyz}\left(v_x,v_y,v_z\right)\), que es solo la fracción de todas las moléculas cuyos respectivos componentes de velocidad cartesiana son menores que\(v_x\),\(v_y\),\(v_z\). Ya que\(f_x\left(v_x\right)\)\(f_y\left(v_y\right)\),, y\(f_z\left(v_z\right)\) son las fracciones cuyos componentes son menores que\(v_x\)\(v_y\),, y\(v_z\), respectivamente, su producto es igual a\(f_{xyz}\left(v_x,v_y,v_z\right)\) Tenemos\(f_{xyz}\left(v_x,v_y,v_z\right)=f_x\left(v_x\right)f_y\left(v_y\right)f_z\left(v_z\right)\). Para la velocidad de una molécula seleccionada al azar\(\left(v^*_x,v^*_y,v^*_z\right)\),, para ser incluida en la fracción representada por\(f_{xyz}\left(v_x,v_y,v_z\right)\), la velocidad debe estar en el rango particular\({ + \mathrm{\infty }\mathrm{<}v}^{\mathrm{*}}_x\mathrm{<}v_x\),\( + \mathrm{\infty }\mathrm{<}v^{\mathrm{*}}_y\mathrm{<}v_y\), y\({ + \mathrm{\infty }\mathrm{<}v}^{\mathrm{*}}_z\mathrm{<}v_z\).
Sin embargo, para\(v^*_x\) que se incluya una velocidad\(f_x\left(v_x\right)\), debemos tener\(v^*_x<v_x\),\(v^*_y<\infty\), y\(v^*_z<\infty\); es decir, los componentes\(v^*_y\) y\(v^*_z\) puede tener cualquier valor. Dado que la probabilidad de que\(v_x\)\(v_y\),, y\(v_z\) satisfacer\(v^*_x<v_x\),\(v^*_y<v_y\), y\(v^*_z<v_z\) es
\[\begin{aligned} P\left(v^*_x<v_x,v^*_y<v_y,v^*_z<v_z\right) & = f_{xyz} \left(v_x,v_y,v_z \right) \\ ~ & = f_x (v_x)f_y(v_y)f_z(v_z) \end{aligned}\]
la probabilidad que\(v^*_x\) se incluye en\(f_x\left(v_x\right)\) se convierte
\[ \begin{aligned} P\left(v^*_x<v_x,v^*_y< \infty, v_z^* < \infty \right) & = f_{xyz} \left( v_x, \infty, \infty \right) \\ ~ & = f_x \left( v_x \right) f_y \left( \infty \right) f_z \left( \infty \right) \\ ~ & = f_x \left( v_x \right) \end{aligned}\]
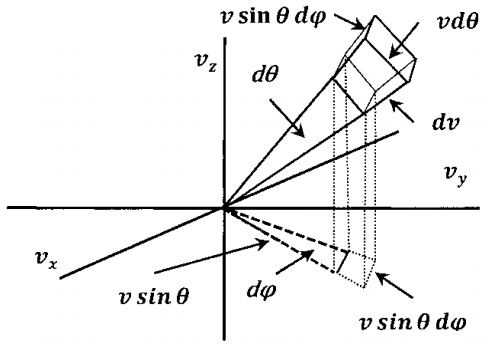
Para nuestros propósitos, necesitamos ser capaces de expresar la probabilidad de que la velocidad se encuentre dentro de cualquier rango de velocidades. Utilicemos\(\mathrm{\textrm{ʋ}}\) para designar una región particular de “volumen” en el espacio de velocidad y usar\(P\left(\mathrm{\textrm{ʋ}}\right)\) para designar la probabilidad de que la velocidad de una molécula seleccionada aleatoriamente esté en esta región. Cuando dejamos que sea la región en el espacio de velocidad en la que\(x\) -componentes se encuentran entre\(v_x\)
y\(v_x+dv_x\),\(y\) -componentes se encuentran entre\(v_y\), y\(v_y+dv_y\), y\(z\) -los componentes se encuentran entre\(v_z\) y\(v_z+dv_z\),\(dP\left(\textrm{ʋ}\right)\) denota la probabilidad de que la velocidad de una molécula elegida aleatoriamente\(\ \left(v^*_x,v^*_y,v^*_z\right)\),, satisfaga las condiciones\(v_x<v^*_x<v_x+dv_x\),\(v_y<v^*_y<v_y+dv_y\), y \(v_z<v^*_z<v_z+dv_z\).
\(dP\left(\textrm{ʋ}\right)\)es un incremento de probabilidad. La\(\ dP\left(\textrm{ʋ}\right)\) dependencia de\(v_x\),\(v_y\),\(v_z\),\({dv}_x\),\(dv_y\),, y\(dv_z\) puede hacerse explícita introduciendo una nueva función,\(\rho \left(v_x,v_y,v_z\right)\), definida por
\[dP\left(\textrm{ʋ}\right)=\rho \left(v_x,v_y,v_z\right)dv_xdv_ydv_z\]
Dado que\(dv_xdv_ydv_z\) es el volumen disponible en el espacio de velocidad para velocidades cuyos\(x\) -componentes están entre\(v_x\) y\(v_x+dv_x\), cuyos\(y\) -componentes están entre\(v_y\)\(v_y+dv_y\), y, y cuyos\(z\) -componentes están entre\(v_z\) y\(v_z+dz\), vemos que \(\rho \left(v_x,v_y,v_z\right)\)es una función de densidad de probabilidad en tres dimensiones. El valor de\(\rho \left(v_x,v_y,v_z\right)\) es la probabilidad, por unidad de volumen en el espacio de velocidad, de que una molécula tenga la velocidad\(\left(v_x,v_y,v_z\right)\). Para cualquier velocidad,\(\left(v_x,v_y,v_z\right)\), hay un valor de\(\rho \left(v_x,v_y,v_z\right)\); este valor es sólo un número. Si queremos la probabilidad de encontrar una velocidad dentro de algún pequeño volumen de velocidad espacial alrededor\(\left(v_x,v_y,v_z\right)\), podemos encontrarla multiplicando\(\rho \left(v_x,v_y,v_z\right)\) por este volumen.
A partir de las funciones unidimensionales de probabilidad-densidad, la probabilidad de que el\(x\) -componente de una velocidad molecular se encuentre entre\(v_x\) y\(v_x+dv_x\), es justo\(\left({{df}_x\left(v_x\right)}/{dv_x}\right)dv_x\), cualesquiera que sean los valores de\(v_y\) y\(v_z\). La probabilidad de que el\(y\) -componente se encuentre entre\(v_y\) y\(v_y+dv_y\), es justo\(\left({{df}_y\left(v_y\right)}/{dv_y}\right)dv_y\), cualesquiera que sean los valores de\(v_x\) y\(v_z\). La probabilidad de que el\(z\) -componente se encuentre entre\(v_z\) y\(v_z+dv_z\), es justo\(\left({df_z\left(v_z\right)}/{dv_z}\right)dv_z\), cualesquiera que sean los valores de\(v_x\) y\(v_y\). Cuando interpretamos la suposición de Maxwell en el sentido de que estas son probabilidades independientes, la probabilidad de que las tres condiciones se realicen simultáneamente es
\[dP\left(\textrm{ʋ}\right)=\left(\frac{df_x\left(v_x\right)}{dv_x}\right)\left(\frac{df_y\left(v_y\right)}{{dv}_y}\right)\left(\frac{{df}_z\left(v_z\right)}{{dv}_z}\right)dv_xdv_ydv_z=\rho \left(v_x,v_y,v_z\right)dv_xdv_ydv_z\]
Evidentemente, el producto de estas densidades de probabilidad tridimensionales es la densidad de probabilidad tridimensional. Tenemos\[\rho \left(v_x,v_y,v_z\right)=\left(\frac{df_x\left(v_x\right)}{dv_x}\right)\left(\frac{df_y\left(v_y\right)}{{dv}_y}\right)\left(\frac{{df}_z\left(v_z\right)}{{dv}_z}\right)={\rho }_x\left(v_x\right){\rho }_y\left(v_y\right){\rho }_z\left(v_z\right)\]
De la suposición de Maxwell, hemos derivado la conclusión que se\(\rho \left(v_x,v_y,v_z\right)\) puede expresar como un producto de las densidades de probabilidad unidimensionales\(\left({df\left(v_x\right)}/{dv_x}\right)dv_x\),\(\left({df\left(v_y\right)}/{dv_y}\right)dv_y\), y\(\left({df\left(v_z\right)}/{dv_z}\right)dv_z\). Como estas son densidades de probabilidad, tenemos
\[\int^{\infty }_{-\infty }{\left(\frac{{df}_x\left(v_x\right)}{dv_x}\right)}dv_x=\int^{\infty }_{-\infty }{\left(\frac{{df}_y\left(v_y\right)}{dv_y}\right)}dv_y=\int^{\infty }_{-\infty }{\left(\frac{{df}_z\left(v_z\right)}{dv_z}\right)}dv_z=1\]y\[\mathop{\int\!\!\!\!\int\!\!\!\!\int}\nolimits^{\infty }_{-\infty }{\rho \left(v_x,v_y,v_z\right){dv}_xdv_y}dv_z=1\]
Además, porque las coordenadas cartesianas difieren entre sí solo en orientación,\(\left({df\left(v_x\right)}/{dv_x}\right)dv_x\),\(\left({df\left(v_y\right)}/{dv_y}\right)dv_y\), y\(\left({df\left(v_z\right)}/{dv_z}\right)dv_z\) deben ser todas la misma función.
Para resumir el desarrollo anterior, definimos\(\rho \left(v_x,v_y,v_z\right)\) independientemente de\({df_x\left(v_x\right)}/{dv_x}\),\({df_y\left(v_y\right)}/{dv_y}\), y\({df_z\left(v_z\right)}/{dv_z}\). Entonces, a partir de la suposición de Maxwell de que las probabilidades tridimensionales son independientes, encontramos\[\rho \left(v_x,v_y,v_z\right)=\left(\frac{df_x\left(v_x\right)}{dv_x}\right)\left(\frac{df_y\left(v_y\right)}{{dv}_y}\right)\left(\frac{{df}_z\left(v_z\right)}{{dv}_z}\right)\]\[={\rho }_x\left(v_x\right){\rho }_y\left(v_y\right){\rho }_z\left(v_z\right)\]
Alternativamente, podríamos tomar la suposición de Maxwell como que la función de densidad de probabilidad tridimensional es expresable como un producto de densidades de probabilidad tridimensionales:
\[\rho \left(v_x,v_y,v_z\right) ={\rho }_x\left(v_x\right){\rho }_y\left(v_y\right){\rho }_z\left(v_z\right)\]
En este caso, las relaciones de\({\rho }_x\left(v_x\right)\)\({\rho }_y\left(v_y\right)\), y\({\rho }_z\left(v_z\right)\), con las probabilidades acumulativas unidimensionales (\(f_x\left(v_x\right)\), etc.) deben deducirse de las propiedades de\(\rho \left(v_x,v_y,v_z\right)\). Como se enfatizó anteriormente, nuestra deducción\(f_x\left(v_x\right)\) de datos experimentales utiliza\(v_x\) valores que están asociados con todos los valores posibles de\(v_y\) y\(v_z\). Es decir, lo que determinamos en nuestro experimento (hipotético) es
\[ \begin{aligned} f_x\left(v_x\right) & =\int^{v_x}_{v_x=-\infty}{\mathop{\int\!\!\!\!\int}\nolimits^{\infty}_{v_{y,z} = -\infty }{\rho \left(v_x,v_y,v_z\right){dv}_xdv_ydv_z}} \\ & =\int^{v_x}_{-\infty} \rho_x \left(v_x\right)dv_x\int^{\infty}_{-\infty} \rho_y \left(v_y\right) dv_y\int^{\infty}_{-\infty} \rho_z \left(v_z\right) dv_z \\ & =\int^{v_x}_{-\infty} \rho_x \left(v_x\right) dv_x \end{aligned}\]
de lo que se deduce que
\[\frac{{df}_x\left(v_x\right)}{{dv}_x}={\rho }_x\left(v_x\right)\]