9.26: Problemas

Problemas

1. ¿Una máquina de movimiento perpetuo de segundo tipo viola el principio de conservación de energía?

2. ¿De qué es lo contrapositivo\(\left(\mathrm{SL\ and}\ \sim \mathrm{MSL}\right)\Rightarrow \left(\Delta \hat{S}<0\right)\)? Es un teorema de lógica que\(\sim (\mathrm{B\ and\ C})\Rightarrow (\sim B{\mathrm{and}}/{\mathrm{or}}\sim \mathrm{C})\). Interpretar este teorema. Dado que SL es cierto y eso\(\sim \left(\mathrm{SL\ and}\ \sim \mathrm{MSL}\right)\) es cierto, probar que\(\sim \mathrm{MSL}\) es cierto.

3. Max Planck presentó el siguiente enunciado de la segunda ley:

“Es imposible construir un motor que funcione en un ciclo completo, y no produzca ningún efecto excepto la elevación de un peso y el enfriamiento de un depósito de calor”.

(M. Planck, Tratado sobre Termodinámica, 3a Edición, traducido de la séptima edición alemana, Dover Publications, Inc., p. 89.) Dado que tomamos que “elevar un peso” sea equivalente a “produce trabajo en los alrededores”, la declaración de Planck difiere de nuestra declaración basada en máquinas solo en que permite que la temperatura de la fuente de calor disminuya a medida que avanza la producción de trabajo. Ahora podemos preguntarnos si esta diferencia tiene consecuencias materiales. En particular, ¿podemos probar que la declaración de Planck implica nuestra declaración basada en máquinas, o viceversa? (Sugerencia: Supongamos que tenemos máquinas idénticas tipo Planck, cada una con su propio depósito de calor. Disipamos por fricción el trabajo producido por una máquina en el depósito de calor de la otra.)

4. Nuestros enunciados de la primera y segunda ley tienen un formato común: Afirmación de que existe una función estatal; definición operativa por la cual se puede medir la función estatal; declaración de una propiedad exhibida por esta función estatal. Expresar la ley cero-ésima de la termodinámica (Capítulo 1) en este formato.

5. Una muestra de 0.400 mol de\(N_2\) se comprime de 5.00 L a 2.00 L, mientras que la temperatura se mantiene constante a 350 K. Supongamos que\(N_2\) es un gas ideal. Calcular el cambio en la energía libre de Helmholtz,\(\Delta A\).

6. Demostrar que\(\Delta G=\Delta A\) cuando un gas ideal sufre un cambio a temperatura constante.

7. Calcular\(\Delta E\)\(\Delta H\),, y\(\Delta G\) para el proceso en problema 5.

8. Una muestra de 0.200 mol de un gas ideal, inicialmente a 5.00 bar, se expande reversible e isotérmicamente de 1.00 L a 10.00 L. Calcular\(\Delta E\),\(\Delta H\), y\(\Delta G\) para este proceso.

9. Una muestra de 100.0 g de tetracloruro de carbono se comprime de 1.00 bar a 10.00 bar a una temperatura constante de 20 C. A 20 C, el tetracloruro de carbono es un líquido cuya densidad es\(1.5940\ \mathrm{g}\ \mathrm{m}{\mathrm{L}}^{-1}\). Supongamos que la densidad no cambia significativamente con la presión. ¿Qué es\(\Delta G\) para este proceso?

10. Calcular el cambio de energía libre de Helmholtz (\(\Delta A\)) en el problema 9.

11. Si\(C_V\) es constante, mostrar que las temperaturas y volúmenes iniciales y finales para una expansión adiabática ideal-gas están relacionados por la ecuación\[\left(\frac{T_f}{T_i}\right)=\left(\frac{V_i}{V_f}\right)^{R/C_V}\]

12. A 25 C, el volumen inicial de un gas ideal monatómico es de 5 L a 10 bar. Este gas se expande a 20 L contra una presión constante aplicada de 1 bar.

a) ¿Es este proceso imposible, espontáneo o reversible?

b) ¿Cuál es la temperatura final?

(c) Encontrar\(q\),\(w\),\(\Delta E\), y\(\Delta H\) para este proceso.

13. El mismo cambio de experiencia de estado por el gas ideal monatómico en el problema 12 se puede efectuar en dos etapas. Dejar que el paso A sea el enfriamiento reversible del gas a su temperatura final mientras que la presión se mantiene constante a 10 bar. Deje que el paso B sea la expansión isotérmica reversible del gas resultante a una presión de 1 bar.

a) Encontrar\(q\),,\(w\)\(\Delta E\), y\(\Delta H\) para el paso A.

b) Encontrar\(q\),,\(w\)\(\Delta E\), y\(\Delta H\) para la etapa B.

(c) A partir de sus resultados en (a) y (b)\(\ q\), encontrar\(w\),\(\Delta E\), y\(\Delta H\) para el proceso general del paso A seguido del paso B.

(d) Compara los valores de\(q\),\(w\),\(\Delta E\), y\(\Delta H\) que encuentras en (c) con los valores para el mismo proceso general que encontraste en el problema 12.

(e) Encontrar\(\Delta S\) y\(\Delta \hat{S}\) para el paso A.

f) Encontrar\(\Delta S\) y\(\Delta \hat{S}\) para el paso B.

g) Encontrar\(\Delta S\)\(\Delta \hat{S}\), y\(\Delta S_{universe}\) para el proceso general.

14. Supongamos que el proceso en el problema 12 ocurre mientras el gas está en contacto térmico con su entorno y que la temperatura del entorno siempre es igual a la temperatura final del gas. Encuentra\(\Delta \hat{S}\) y\(\Delta S_{universe}\) para este proceso.

15. A 25 C, el volumen inicial de un gas ideal monatómico es de 5 L a 10 bar. El gas se expande a 20 L mientras está en contacto térmico con el entorno a 125 C. Durante la expansión, la presión aplicada es constante e igual a la presión de equilibrio en el volumen y temperatura finales.

a) ¿Es este proceso imposible, espontáneo o reversible?

b) Encontrar\(q\),,\(w\)\(\Delta E\),\(\Delta H\), y\(\Delta \hat{S}\) para este proceso.

(c) Encontrar\(\Delta S\) y\(\Delta S_{universe}\) para este proceso. Para encontrar\(\Delta S\), es necesario encontrar una ruta alternativa reversible que efectúe el mismo cambio en las funciones de estado del sistema.

16. A 60 C, la densidad del agua es\(\mathrm{0.98320\ g}\ {\mathrm{cm}}^{-3}\), la presión de vapor es de 19,932 Pa, y la entalpía de vaporización es\(42,482\mathrm{\ J}\ {\mathrm{mol}}^{-1}\). Supongamos que el agua gaseosa se comporta como un gas ideal. Un recipiente que contiene agua líquida y gaseosa se coloca en un baño constante de 60 C, y la presión aplicada se mantiene en 19,932 Pa mientras se vaporizan 100 g de agua.

a) ¿Es este proceso imposible, espontáneo o reversible?

b) Encontrar\(q\),,\(w\),\(\Delta E\)\(\Delta H\),\(\Delta S\),\(\Delta A\), y\(\Delta G\) para este proceso.

c) ¿Es\({\left(\Delta S\right)}_{EV}=0\) un criterio de equilibrio que se aplica a este sistema? ¿Por qué o por qué no? \({\left(\Delta H\right)}_{SP}=0\)? \({\left(\Delta A\right)}_{VT}=0\)? \({\left(\Delta G\right)}_{PT}=0\)?

17. Este problema compara la eficiencia y\(\sum{q/T}\) para un mol de un gas monatómico ideal tomado alrededor de un ciclo reversible de Carnot con las mismas cantidades para el mismo gas tomadas alrededor de un ciclo irreversible utilizando los mismos dos depósitos de calor.

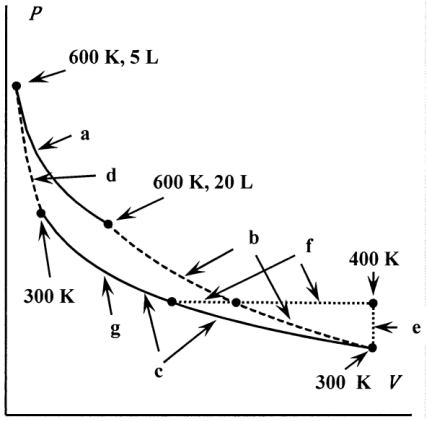
(i) Dejar que la etapa sucesiva del ciclo reversible de Carnot sea a, b, c y d. La etapa isotérmica a comienza con el gas ocupando 5.00 L a 600 K y termina con el gas ocupando 20.00 L. La etapa de expansión adiabática b termina con el gas a 300 K. Después de la etapa de compresión isotérmica c, el gas se comprime adiabáticamente en el paso d al estado original. Encuentra\(P\),\(V\), y\(T\) para el gas al final de cada paso de este ciclo reversible. Encontrar\(\sum q/\hat{T}\),\(\Delta S\), y\(\Delta \hat{S}\) para el ciclo a, b, c, d. ¿Cuál es la eficiencia de este ciclo?

(ii) Supongamos que siguiendo la etapa b, el gas ideal se calienta a volumen constante a 400 K intercambiando calor con el reservorio de 600 K. Llame a este paso e. Siguiendo la etapa e, el gas se enfría a presión constante a 300 K por contacto con el depósito de 300 K. Llame a este paso f. Siguiendo el paso f, el gas se comprime isotérmicamente y reversiblemente a 300 K al mismo\(P\),\(V\), y a\(T\) medida que el gas alcanza al final de la etapa c. Llame a este paso g. Buscar\(P\),\(V\), y\(T\) para el gas en los extremos de los pasos e, f, y g. Aunque las etapas e y f no son reversibles, los mismos cambios se pueden efectuar reversiblemente manteniéndose a\(T=\hat{T}\) medida que el gas se calienta a volumen constante (etapa e) y se enfría a presión constante (etapa f). (Discutimos este punto más adelante en la Sección 12.4.) En consecuencia,\({\Delta }_eS=\int^{400\ K}_{300\ K} \frac{C_V}{T}dT\) y\({\Delta }_fS=\int^{400\ K}_{300\ K} \frac{C_P}{T}dT\). Encontrar\(\sum q/\hat{T}\),\(\Delta S\), y\(\Delta \hat{S}\), y\(\Delta S_{universe}\) para el ciclo a, b, e, f, g, d. ¿Cuál es la eficiencia de este ciclo?

(iii) Comparar el valor de lo\(\sum q/ \hat{T}\) que obtuvo en la parte (ii) con el valor del\(\sum q/ \hat{T}\) que obtuvo en la parte (i).

(iv) El teorema de Clausius afirma que\(\sum q/ \hat{T}=0\) para un ciclo atravesado reversiblemente, y\(\sum q/ \hat{T}<0\) para un ciclo atravesado espontáneamente. Comentar.

18. Para un ciclo espontáneo atravesado mientras la temperatura cambia continuamente, el teorema de Clausius lo afirma\(\oint{dq/\hat{T}}<0\). Demostrar que esta desigualdad se deriva del resultado,\(dS>dq/ \hat{T}\), que obtuvimos en la Sección 9.15 para cualquier proceso espontáneo en un sistema cerrado.

19. En las Secciones 9.6 a 9.8 concluimos que\(\Delta S+\Delta \hat{S}=0\) es necesario para un proceso reversible,\(\Delta S+\Delta \hat{S}>0\) es necesario para un proceso espontáneo y\(\Delta S+\Delta \hat{S}<0\) es necesario para un proceso imposible. Es decir:\[(\mathrm{Process\ is\ reversible})\ \ \ \Rightarrow \ \left(\Delta S+\Delta \hat{S}=0\right)\] (\(\mathrm{Process\ is\ spontaneous}\))\(\ \ \Rightarrow \left(\Delta S+\Delta \hat{S}>0\right)\), y (\(\mathrm{Process\ is\ impossible}\))\(\ \ \Rightarrow \left(\Delta S+\Delta \hat{S}<0\right)\).

Ya que hemos definido las categorías reversibles, espontáneas e imposibles para que sean exhaustivas y mutuamente excluyentes, la siguiente proposición es cierta:

\[\sim \left(\mathrm{Process\ is\ spontaneous}\right)\ \mathrm{and}\ \sim \left(\mathrm{Process\ is\ impossible}\right)\]\[\Rightarrow \left(\mathrm{Process\ is\ reversible}\right)\]

a) Demostrar que\(\Delta S+\Delta \hat{S}=0\) es suficiente para que el proceso sea reversible; es decir, probar:\[\left(\Delta S+\Delta \hat{S}=0\right)\ \ \Rightarrow \ \ \left(\mathrm{Process\ is\ reversible}\right)\]

b) Demostrar que\(\Delta S+\Delta \hat{S}>0\) es suficiente para que el proceso sea espontáneo; es decir, probar:\[\left(\Delta S+\Delta \hat{S}>0\ \right)\ \Rightarrow \ \ \left(\mathrm{Process\ is\ spontaneous}\right)\]

c) Demostrar que\(\Delta S+\Delta \hat{S}<0\) es suficiente para que el proceso sea imposible; es decir, probar:\[\left(\Delta S+\Delta \hat{S}<0\right)\ \ \Rightarrow \ \ \left(\mathrm{Process\ is\ impossible}\right)\]

20. Etiquete los pasos sucesivos en un ciclo reversible de Carnot A, B, C y D, donde A es el punto en el que la presión es mayor.

(a) Esbozar el camino ABCD en\(P\) —\(V\) espacio.

b) Esbozar el camino ABCD en\(T\) —\(dq^{rev}/T\) espacio.

(c) Esbozar el camino ABCE en\(T\) —\(q^{rev}\) espacio.

d) Esbozar el camino BCDA en\(T\) —\(q^{rev}\) espacio.

(e) Esbozar el camino CDAB en\(T\) —\(q^{rev}\) espacio.

d) Esbozar el camino DABC en\(T\) —\(q^{rev}\) espacio.

21. Supongamos que la atmósfera terrestre es nitrógeno puro y que se comporta como un gas ideal. Supongamos que la energía molar de este nitrógeno es constante y que sus cambios de entropía molar son modelados adecuadamente por\(d\overline{S}=\left({C_V}/{T}\right)dT+\left({R}/{\overline{V}}\right)d\overline{V}\). Para esta atmósfera, muestran que\[{\left(\frac{\partial T}{\partial h}\right)}_E=\frac{-\overline{M}g}{C_V}\] donde\(h\) está la altura sobre la superficie terrestre,\(\overline{M}\) está la masa molar de dinitrogen (\(0.0280\ \ \mathrm{kg}\ {\mathrm{mol}}^{-1}\)),\(g\) es la aceleración por gravedad (\(\mathrm{9.80}\ \mathrm{m}\ {\mathrm{s}}^{-1}\)), y\(C_V\) es la capacidad calorífica de volumen constante (\(20.8\ \mathrm{J}\ {\mathrm{K}}^{-1}\ {\mathrm{mol}}^{-1}\)). [Sugerencia: Escribir el diferencial total para\(\overline{E}=\overline{E}\left(\overline{S},\overline{V},h\right)\). ¿Qué son\({\left({\partial \overline{E}}/{\partial \overline{S}}\right)}_{\overline{V},h}\)\({\left({\partial \overline{E}}/{\partial \overline{V}}\right)}_{\overline{S},h}\), y\({\left({\partial \overline{E}}/{\partial h}\right)}_{\overline{S},\overline{V}}\)?]

Si la temperatura al nivel del mar es de 300 K, ¿cuál es la temperatura en la cima de una montaña de 3000 m?

22. Supongamos que la atmósfera terrestre es nitrógeno puro y que se comporta como un gas ideal. Supongamos que la entalpía molar de este nitrógeno es constante y que sus cambios de entropía molar son modelados adecuadamente por\(d\overline{S}=\left({C_P}/{T}\right)dT-\left({R}/{P}\right)dP\). Para esta atmósfera, muestran que\[{\left(\frac{\partial T}{\partial h}\right)}_S=\frac{-\overline{M}g}{C_P}\] donde\(h\) está la altura sobre la superficie terrestre,\(\overline{M}\) está la masa molar de dinitrogen (\(0.0280\ \ \mathrm{kg}\ {\mathrm{mol}}^{-1}\)),\(g\) es la aceleración por gravedad (\(\mathrm{9.80}\ \mathrm{m}\ {\mathrm{s}}^{-1}\)), y\(C_P\) es la capacidad calorífica de presión constante (\(29.1\ \mathrm{J}\ {\mathrm{K}}^{-1}\ {\mathrm{mol}}^{-1}\)). [Sugerencia: Escribir el diferencial total para\(\ \overline{H}=\overline{H}\left(\overline{S},P,h\right)\). ¿Qué son\({\left({\partial \overline{H}}/{\partial \overline{S}}\right)}_{P,h}\)\({\left({\partial \overline{H}}/{\partial P}\right)}_{\overline{V},h}\), y\({\left({\partial \overline{H}}/{\partial h}\right)}_{\overline{S},\overline{V}}\)?]

Usa esta aproximación para calcular la temperatura en la cima de una montaña de 3000 m cuando la temperatura al nivel del mar es de 300 K.

23. Los excursionistas suelen decir que, como regla general, la temperatura en una montaña disminuye en 1 C por cada aumento de elevación de 100 m. ¿Esta regla está de acuerdo con las relaciones desarrolladas en los problemas 21 y 22? En estos problemas, suponemos que la temperatura de una atmósfera de gas ideal varía con la altitud pero que la energía molar o entalpía no lo hace. ¿Esta suposición contradice el principio de que la energía y la entalpía de un gas ideal dependen únicamente de la temperatura?

24. Derivar la fórmula barométrica (Sección 2.10) a partir de los supuestos de que la atmósfera terrestre es un gas ideal cuya masa molar es\(\overline{\boldsymbol{M}}\) y cuya temperatura y energía libre de Gibbs son independientes de la altitud.

25. Al funcionar a la inversa, un motor Carnot consume trabajo\(\left(w>0\right)\) y transfiere calor\(\left(q_{\ell }>0\right)\) de un depósito de baja temperatura a un depósito de alta temperatura\(\left(q_h<0\right)\). El trabajo realizado por la máquina se convierte en calor que se descarga al depósito de alta temperatura. En un ciclo de la máquina,\(\Delta E=q_{\ell }+q_h=0\). Para un refrigerador, o para una bomba de calor que opera en modo de aire acondicionado, estamos interesados en la cantidad de calor eliminado\(\left(q_{\ell }\right)\) por unidad de energía gastada\(\left(w\right)\). Definimos el coeficiente de desempeño como\(COP\left(cooling\right)={q_{\ell }}/{w}\). Esto es como máximo para el motor reversible Carnot. Demostrar que el máximo teórico es\[COP\left(cooling\right)=\frac{1-\epsilon }{\epsilon }=\frac{T_{\ell }}{T_h-T_{\ell }}\] donde\(\epsilon\) está la eficiencia reversible del automóvil-motor,\[\epsilon =1-\frac{T_{\ell }}{T_h}\] 26. Para una bomba de calor que opera en modo de calefacción, como “horno”, nos interesa la cantidad de calor entregado al espacio que se calienta\(\left(-q_h\right)\) por unidad de energía gastada\(\left(w\right)\). Definimos el coeficiente de desempeño como\(COP\left(heating\right)=-{q_h}/{w}\). Demostrar que el máximo teórico es\[COP\left(heating\right)=\frac{1}{\epsilon }=\frac{T_h}{T_h-T_{\ell }}\]

27. Para\(T_{\ell }=300\ \mathrm{K}\) y\(T_h=500\ \mathrm{K}\), calcular los máximos teóricos para\(COP\left(cooling\right)\) y\(COP\left(heating\right)\).

28. Encuentre el máximo teórico\(COP\left(cooling\right)\) para un refrigerador en\(40\ \mathrm{F}\) en una habitación en\(72\ \mathrm{F}\).

29. Encuentra el máximo teórico\(COP\left(cooling\right)\) para una bomba de calor que mantiene una habitación\(72\ \mathrm{F}\) cuando la temperatura exterior es\(100\ \mathrm{F}\).

30. Encuentra el máximo teórico\(COP\left(heating\right)\) para una bomba de calor que mantiene una habitación\(72\ \mathrm{F}\) cuando la temperatura exterior es\(32\ \mathrm{F}\).

Notas

\({}^{1}\)Para una introducción al concepto de entropía interna y sus aplicaciones, véase Ilya Prigogine, Introducción a la termodinámica de los procesos irreversibles, Interscience Publishers, 1961.