3.E: Ejercicios

Q1

En 1913 Niels Bohr propuso un modelo para el átomo de hidrógeno que da la expresión correcta para los niveles de energía E _n. Su modelo se basaba en un matrimonio incómodo de la mecánica clásica y, en ese momento, en la nueva idea de cuantificación. En el modelo de Bohr del átomo de hidrógeno se supone que el electrón se mueve en órbita circular alrededor del núcleo, como se ilustra en la Fig. 3-7. La energía del electrón en tal órbita es: (1)

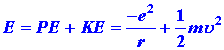
donde u es la velocidad tangencial del electrón en la órbita. Dado que la órbita circular va a ser estable, la atractiva fuerza culomba ejercida sobre el electrón por el núcleo debe ser equilibrada por una fuerza centrífuga, o: (2)

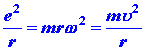
donde w es la velocidad circular del electrón. Hasta este punto el modelo es completamente clásico en concepto. Sin embargo, Bohr postuló ahora que solo se permiten aquellas órbitas para las cuales el momento angular es un múltiplo integral de (h /2 p). Es decir, Bohr postuló que se cuantifica el momento angular del electrón en el átomo de hidrógeno. Este postulado da una ecuación adicional: (3)

1. Demostrar que al eliminar r y u de estas tres ecuaciones se puede obtener la expresión correcta para E _n.
2. Mostrar que el modelo de Bohr predice correctamente que el KE = -½ PE.
3. Mostrar que el radio de la primera órbita de Bohr es idéntico al valor máximo de r para el nivel n = 1 del átomo de hidrógeno,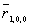, calculado por la mecánica cuántica.
4. Criticar el modelo de Bohr a la luz de los resultados mecánicos cuánticos para el átomo de hidrógeno.

Q2

La parte del espectro de átomos de hidrógeno que ocurre en la región visible surge de electrones en niveles excitados que caen al nivel n = 2. La expresión mecánica cuántica para las frecuencias en este caso, correspondiente a la ecuación (3) del texto para la serie Lyman, es: (4)

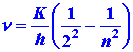
La energía de un fotón emitido para un salto del nivel n al nivel 2 es: (5)

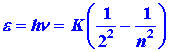
La ecuación (5) predice que una gráfica de las energías fotónicas versus (1/n ²) debe ser una línea recta. Además, predice que la intercepción de esta línea con el eje de energía, correspondiente al valor de 1/n ² = 0, es decir, n = ¥, debe ser igual a (¼) K donde: (6)

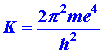
El objetivo de este problema es poner a prueba estas predicciones teóricas frente a los resultados experimentales.

Experimentalmente medimos la longitud de onda de la luz emitida por medio de una rejilla de difracción. Se puede hacer una rejilla para la difracción de luz visible marcando una placa de vidrio con líneas paralelas, igualmente espaciadas. Hay alrededor de 10,000 líneas por cm. Las separaciones entre las líneas en la rejilla d son, por lo tanto, de aproximadamente 1 '10 ^-4 cm que es el orden de magnitud de la longitud de onda de la luz visible. La ecuación de difracción es: (7)

como se discutió anteriormente en el Problema I-1. Medimos el ángulo q para diferentes órdenes n = 1, 2, 3,... del haz de luz difractado. Dado que d es conocido, l puede calcularse. Los valores medidos experimentalmente para las cuatro primeras líneas de la serie Balmer se dan a continuación.

Serie Balmer

l (Å)	n
6563	3
4861	4
4341	5
4102	6

El valor del número cuántico principal n que aparece en la ecuación (5) se da por cada valor de l. (Esta n no está totalmente relacionada con la n de la ecuación (7) para la determinación experimental de l.) Calcular la energía de cada fotón a partir del valor de su longitud de onda.

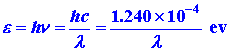
Trazar las energías fotónicas versus el valor apropiado de 1/n ². Deje que el eje 1/n ² corra de 0 a 0.25 y el eje de energía corra de 0 a 3.6 ev. Incluya como punto en su gráfica e = 0 para 1/n ² = 0.25, es decir, cuando n = 2, coinciden el nivel excitado y el nivel al que cae el electrón.

1. ¿Los puntos caen en línea recta como se predijo?
2. Determine el valor de K extendiendo la línea para interceptar el eje de energía. Esta intercepción debe ser igual a K/4. Lee este valor de tu gráfica.
3. Comparar el valor experimental para K con el predicho teóricamente por la ecuación (5). Usa e = 4.803 '10 ^-10 esu, expresa m y h en unidades cgs y el valor de K estará en ergs (1 erg = 6.2420' 10 ¹¹ ev). Recordemos que K es el potencial de ionización para el átomo de hidrógeno. Un electrón que cae del nivel n = ¥ al nivel n = 2 caerá solo (¼) K en energía como es evidente a partir del diagrama de niveles de energía que se muestra en la Fig. 3-2.

Q3

Un haz de átomos con l = 1 se hace pasar a través de un aparato de haz atómico con el campo magnético dirigido a lo largo de un eje perpendicular a la dirección del haz. El haz no desviado de este experimento ingresa a un segundo aparato de haz en el que el campo magnético se dirige a lo largo de un eje que es perpendicular tanto a la trayectoria del haz como a la dirección del campo en el primer experimento. ¿Este componente del haz original se dividirá en el segundo campo magnético aplicado? Explique por qué cree que será, si ésta es efectivamente su respuesta.