2.1: Evolución del tiempo con un hamiltoniano independiente del tiempo

La evolución temporal del estado de un sistema cuántico se describe mediante la ecuación de Schrödinger dependiente del tiempo (TDSE):

\[i \hbar \frac {\partial} {\partial t} \psi ( \overline {r} , t ) = \hat {H} ( \overline {r} , t ) \psi ( \overline {r} , t ) \label{1.1}\]

\(\hat{H}\)es el operador hamiltoniano que describe todas las interacciones entre partículas y campos, y determina el estado del sistema en el tiempo y el espacio. \(\hat{H}\)es la suma de la energía cinética y potencial. Para una partícula bajo la influencia de un potencial

\[\hat {H} = - \frac {\hbar^{2}} {2 m} \hat {\nabla}^{2} + \hat {V} ( \overline {r} , t ) \label{1.2}\]

El estado del sistema se expresa a través de la función de onda\(\psi ( \overline {r} , t )\). La función de onda es compleja y no se puede observar por sí misma, pero a través de ella obtenemos la densidad de probabilidad

\[P = | \psi ( \overline {r} , t ) |^{2},\]

que caracteriza la distribución espacial de probabilidad para las partículas descritas por\(\hat{H}\) en el tiempo\(t\). Además, se utiliza para calcular el valor de expectativa de un operador\(\hat{A}\)

\[ \begin{align} \langle \hat {A} (t) \rangle &= \int \psi^{*} ( \overline {r} , t ) \hat {A} \psi ( \overline {r} , t ) d \overline {r} \\[4pt] &= \langle \psi (t) | \hat {A} | \psi (t) \rangle \label{1.3} \end{align}\]

Los observables físicos deben ser reales, y por lo tanto corresponderán a los valores de expectativa de los operadores hermitianos (\(\hat {A} = \hat {A}^{\dagger}\)).

Nuestra primera exposición a la dependencia del tiempo en la mecánica cuántica suele ser para el caso específico en el que\(\hat{H}\) se supone que el hamiltoniano es independiente del tiempo\(\hat {H} = \hat {H} ( \overline {r} )\).:. Entonces asumimos una solución con una forma en la que las variables espaciales y temporales en la función de onda son separables:

\[\psi ( \overline {r} , t ) = \varphi ( \overline {r} ) T (t) \label{1.4}\]

\[i \hbar \frac {1} {T (t)} \frac {\partial} {\partial t} T (t) = \frac {\hat {H} ( \overline {r} ) \varphi ( \overline {r} )} {\varphi ( \overline {r} )} \label{1.5}\]

Aquí el lado izquierdo es una función solo del tiempo, y el lado derecho es una función solo del espacio (\(\overline {r}\), o más bien la posición y el impulso). La ecuación\ ref {1.5} solo se puede satisfacer si ambos lados son iguales a la misma constante,\(E\). Tomando el lado derecho tenemos

\[\frac {\hat {H} ( \overline {r} ) \varphi ( \overline {r} )} {\varphi ( \overline {r} )} = E \quad \Rightarrow \quad \hat {H} ( \overline {r} ) \varphi ( \overline {r} ) = E \varphi ( \overline {r} ) \label{1.6}\]

Esta es la Ecuación de Schrödinger Independiente del Tiempo (TISE), una ecuación de valor propio, para la cual\(\varphi ( \overline {r} )\) son los autoestados y\(E\) son los autovalores. Aquí señalamos que

\[\langle \hat {H} \rangle = \langle \psi | \hat {H} | \psi \rangle = E,\]

así\(\hat{H}\) es el operador correspondiente\(E\) y recurriendo a la mecánica clásica que asociamos\(\hat{H}\) con el valor de expectativa de la energía del sistema. Ahora tomando el lado izquierdo de la Ecuación\ ref {1.5} e integrando:

\[\begin{align} i \hbar \frac {1} {T (t)} \frac {\partial T} {\partial t} &= E \\[4pt] \left( \frac {\partial} {\partial t} + \frac {i E} {\hbar} \right) T (t) &= 0 \label{1.7} \end{align}\]

que tiene soluciones como esta:

\[T (t) = \exp ( - i E t / \hbar ) \label{1.8}\]

Entonces, en el caso de un potencial enlazado tendremos un conjunto discreto de funciones propias\(\varphi _ {n} ( \overline {r} )\) con valores propios de energía correspondientes\(E_n\) del TISE, y hay un conjunto de soluciones correspondientes al TDSE.

\[\psi _ {n} ( \overline {r} , t ) = \varphi _ {n} ( \overline {r} ) \underbrace{\exp \left( - i E _ {n} t / \hbar \right)}_{\text{phase factor}} \label{1.9}\]

Factor de Fase

Para cualquier número complejo escrito en forma polar (como\(re^{iθ}\)), el factor de fase es el factor exponencial complejo (\(e^{iθ}\)). El factor de fase no tiene ningún significado físico, ya que la introducción de un factor de fase no cambia los valores de expectativa de un operador hermitiano. Eso es

\[ \langle \phi |A|\phi \rangle = \langle \phi |e^{-i\theta}Ae^{i\theta}|\phi \rangle \]

Dado que la única dependencia del tiempo en\(\psi _ {n} \) es un factor de fase, la densidad de probabilidad para un estado propio es independiente del tiempo:

\[P = \left| \psi _ {n} (t) \right|^{2} = \text {constant}.\]

Por lo tanto, los autoestados\(\varphi ( \overline {r} )\) no cambian con el tiempo y se denominan estados estacionarios.

Sin embargo, más generalmente, un sistema puede existir como una combinación lineal de estados propios:

\[\begin{align} \psi ( \overline {r} , t ) &= \sum _ {n} c _ {n} \psi _ {n} ( \overline {r} , t ) \\[4pt] &= \sum _ {n} c _ {n} e^{- i E _ {n} t h} \varphi _ {n} ( \overline {r} ) \label{1.10} \end{align}\]

donde\(c_n\) se encuentran amplitudes complejas, con

\[\sum _ {n} \left| c _ {n} \right|^{2} = 1. \nonumber\]

Para tal caso, la densidad de probabilidad oscilará con el tiempo. Como ejemplo, considere dos autoestados

\[ \begin{align} \psi ( \overline {r} , t ) &= \psi _ {1} + \psi _ {2} \nonumber \\[4pt] &= c _ {1} \varphi _ {1} e^{- i E _ {1} t / h} + c _ {2} \varphi _ {2} e^{- i E _ {2} t / h} \label{1.11} \end{align}\]

Para este estado la densidad de probabilidad oscila en el tiempo como

\[\begin{align} P (t) & = | \psi |^{2} \nonumber \\[4pt] &= \left| \psi _ {1} + \psi _ {2} \right|^{2} \nonumber \\[4pt] & = \left| c _ {1} \varphi _ {1} \right|^{2} + \left| c _ {2} \varphi _ {2} \right|^{2} + c _ {1}^{*} c _ {2} \varphi _ {1}^{*} \varphi _ {2} e^{- i \left( \alpha _ {2} - \omega _ {1} \right) t} + c _ {2}^{*} c _ {1} \varphi _ {2}^{*} \varphi _ {1} e^{+ i \left( a _ {2} - \omega _ {1} \right) t} \nonumber \\[4pt] & = \left| \psi _ {1} \right|^{2} + \left| \psi _ {2} \right|^{2} + 2 \left| \psi _ {1} \psi _ {2} \right| \cos \left( \omega _ {2} - \omega _ {1} \right) t \label{1.12} \end{align}\]

donde\(\omega _ {n} = E _ {n} / \hbar\). Nos referimos a este estado del sistema que da lugar a esta oscilación dependiente del tiempo en la densidad de probabilidad como un estado de superposición coherente, o coherencia. De manera más general, el término de oscilación en la Ecuación\ ref {1.12} también puede incluir un factor de fase independiente del tiempo\(\phi\) que surge de los coeficientes de expansión complejos.

Como ejemplo, considere la superposición del suelo y los primeros estados excitados del oscilador armónico cuántico. Las funciones de onda base,\(\psi _ {0} (x)\) y\(\psi _ {1} (x)\), y sus densidades de probabilidad estacionarias\(P _ {i} = \left\langle \psi _ {i} (x) | \psi _ {i} (x) \right\rangle\) son

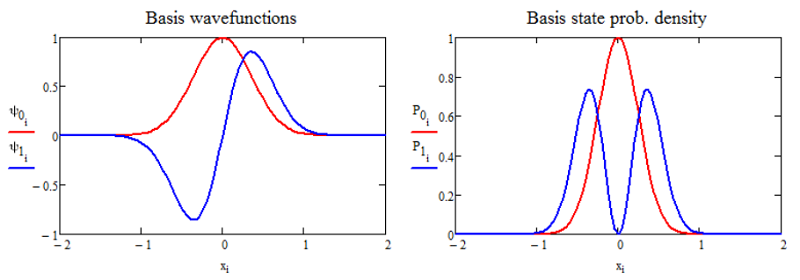
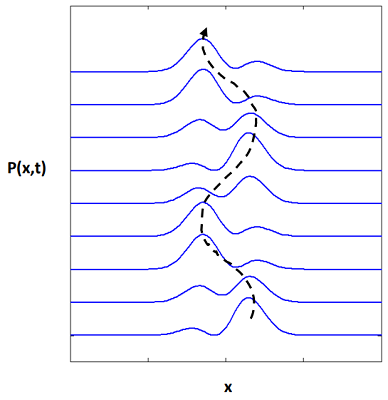
Si creamos una superposición de estos estados con la Ecuación\ ref {1.11}, la densidad de probabilidad dependiente del tiempo oscila, con similitud de\(\langle x (t) \rangle\) rodamiento con el movimiento clásico. (Aquí\(c_0 = 0.5\) y\(c_1 = 0.87\).)

Lecturas

1. Cohen-Tannoudji, C.; Diu, B.; Lalöe, F., Mecánica Cuántica. Wiley-Interscience: París, 1977; p. 405.
2. Nitzan, A., Dinámica Química en Fases Condensadas. Oxford University Press: Nueva York, 2006; Ch. 1.
3. Schatz, G. C.; Ratner, M. A., Mecánica Cuántica en Química. Publicaciones de Dover: Mineola, NY, 2002; Ch. 2.