2.2: Operadores Exponenciales de nuevo

A lo largo de nuestro trabajo, haremos uso de operadores exponenciales de la forma\(\hat {T} = e^{- i \hat {A}}\) Veremos que estos operadores exponenciales actúan sobre una función de onda para moverla en tiempo y espacio. De particular interés para nosotros es el propagador de tiempo u operador de evolución temporal\(\hat {U} = e^{- i \hat {H} t / h},\) que propaga la función de onda en el tiempo. Tenga en cuenta que el operador\(\hat {T}\) es una función de un operador,\(f(\hat{A})\). Una función de un operador se define a través de su expansión en una serie Taylor, por ejemplo

\[\hat {T} = e^{- i \hat {A}} = \sum _ {n = 0}^{\infty} \frac {( - i \hat {A} )^{n}} {n !} = 1 - i \hat {A} - \frac {\hat {A} \hat {A}} {2} - \cdots \label{1.13}\]

Dado que los usamos con tanta frecuencia, revisemos las propiedades de los operadores exponenciales que se pueden establecer con la ecuación\ ref {1.13}. Si el operador\(\hat{A}\) es hermitiano, entonces\(\hat {T} = e^{- i \hat {A}}\) es unitario, es decir,\(\hat {T}^{\dagger} = \hat {T}^{- 1}\). Así el conjugado hermitiano de\(\hat{T}\) invierte la acción de\(\hat{T}\). Para el propagador de tiempo\(\hat{U}\), a menudo\(U^{†}\) se conoce como el operador de inversión de tiempo.

Los estados propios del operador\(\hat{A}\) también son estados propios de\(f(\hat{A})\), y los valores propios son funciones de los valores propios de\(\hat{A}\). Es decir, si conoces los valores propios y los vectores propios de\(\hat{A}\), es decir\(\hat {A} \varphi _ {n} = a _ {n} \varphi _ {n}\), puedes mostrar expandiendo la función que

\[f ( \hat {A} ) \varphi _ {n} = f \left( a _ {n} \right) \varphi _ {n} \label{1.14}\]

Nuestra aplicación más común de esta propiedad será a operadores exponenciales que involucren a los hamiltonianos. Dados los autoestados\(\varphi _ {n}\), entonces\(\hat {H} | \varphi _ {n} \rangle = E _ {n} | \varphi _ {n} \rangle\) implica

\[e^{- i \hat {H} t / \hbar} | \varphi _ {n} \rangle = e^{- i E _ {n} t / \hbar} | \varphi _ {n} \rangle \label{1.15}\]

Así como lo\(\hat {U} = e^{- i \hat {H} t / h}\) es el operador de evolución temporal, que desplaza la función de onda en el tiempo,\(\hat {D} _ {x} = e^{- i \hat {p} _ {x} x / \hbar}\) es el operador de desplazamiento espacial que se mueve\(\psi\) a lo largo de la\(x\) coordenada. Si definimos\(\hat {D} _ {x} ( \lambda ) = e^{- i \hat {p} _ {x} \lambda / h},\) entonces la acción de es desplazar la ondafunción por una cantidad\(\lambda\)

\[| \psi ( x - \lambda ) \rangle = \hat {D} _ {x} ( \lambda ) | \psi (x) \rangle \label{1.16}\]

Además, aplicar\(\hat {D} _ {x} ( \lambda )\) a un operador de posición cambia al operador\(\lambda\)

\[\hat {D} _ {x}^{\dagger} \hat {x} \hat {D} _ {x} = \hat {x} + \lambda \label{1.17}\]

Así\(e^{- i \hat {p} _ {x} \lambda / h} | x \rangle\) es un vector propio de\(\hat{x}\) con valor propio\(x + \lambda\) en lugar de\(x\). El operador\(\hat {D} _ {x} = e^{- i \hat {p} _ {x} \lambda / \hbar}\) es un operador de desplazamiento para coordenadas de\(x\) posición. De igual manera,\(\hat {D} _ {y} = e^{- i \hat {p} _ {y} \lambda / \hbar}\) genera desplazamientos en\(y\) y\(\hat{D}_z\) en\(z\). Similar al propagador de tiempo\(\hat{U}\), el\(hta{D}\) operador de desplazamiento debe ser unitario, ya que la acción de debe dejar el sistema sin cambios. Es decir, si\(\hat{D}\) cambia el sistema a de, luego cambia el sistema de\(x\) atrás a\(x_0\).

Sabemos intuitivamente que los desplazamientos lineales conmutan. Por ejemplo, si queremos desplazar una partícula en dos dimensiones,\(x\) y\(y\), el orden de desplazamiento no importa. Terminamos en la misma posición. Estos operadores de desplazamiento conmutan, como se esperaba de\([\hat{p}_x,\hat{p}_y] = 0\)

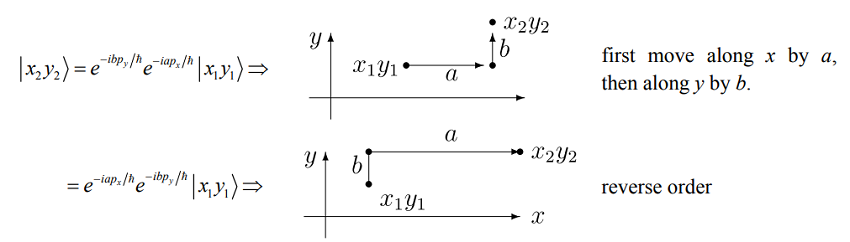
Similar al operador de desplazamiento, podemos definir operadores de rotación que dependen de los operadores de momento angular,\(L_x\),\(L_y\), y\(L_z\). Por ejemplo,\(\hat {R} _ {x} ( \phi ) = e^{- i \phi L _ {x} / \hbar}\) da una rotación por ángulo\(\phi\) alrededor del eje x. A diferencia del desplazamiento lineal, las rotaciones alrededor de diferentes ejes no se desplazan. Por ejemplo, considere un estado que representa una partícula desplazada a lo largo del eje z,\(| \mathrm {Z} 0 \rangle\). Ahora la acción de dos rotaciones\(\hat{R}_x\) y\(\hat{R}_y\) por un ángulo de\(\pi/2\) sobre esta partícula difiere dependiendo del orden de operación.

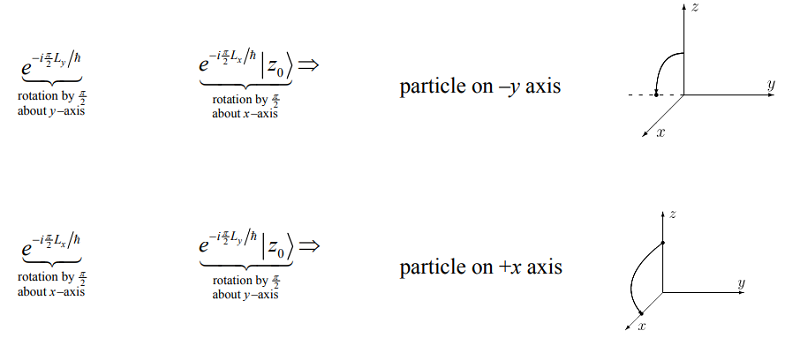
Los resultados de estas dos rotaciones tomadas en orden opuesto difieren por una rotación alrededor del eje z. Por lo tanto, debido a que las rotaciones alrededor de diferentes ejes no se desplazan, debemos esperar que los operadores de momento angular, que generan estas rotaciones, no conmuten. En efecto, sabemos que\([L_x,L_y] = i\hbar L_z\) donde el conmutador de rotaciones alrededor de los ejes x e y está relacionado por una rotación del eje z. Al igual que con los operadores de rotación, tendremos que tener cuidado con los propagadores de tiempo para determinar si el orden de propagación del tiempo importa. Esto, a su vez, dependerá de si los hamiltonianos en dos puntos en el tiempo conmutan.

Propiedades útiles del operador exponencial

Por último, cabe destacar algunas relaciones que son importantes en la evaluación de la acción de los operadores exponenciales:

1. La relación Baker—Hausdorff:\[\left. \begin{array} {r l} {\exp ( i \hat {G} \lambda ) \hat {A} \exp ( - i \hat {G} \lambda ) = \hat {A} + i \lambda [ \hat {G} , \hat {A} ] + \left( \frac {i^{2} \lambda^{2}} {2 !} \right) [ \hat {G} , [ \hat {G} , \hat {A} ] ] + \ldots} \\ {+ \left( \frac {i^{n} \lambda^{n}} {n !} \right) [ \hat {G} , [ \hat {G} , [ \hat {G} , \hat {A} ] ] ] \ldots ]} & {+ \dots} \end{array} \right. \label{1.18}\]
2. Si\(\hat {A}\) y\(\hat {B}\) no se conmuta, sino que se\([ \hat {A} , \hat {B} ]\) desplaza con\(\hat {A}\) y\(\hat {B}\), entonces\[e^{\hat {A} + \hat {B}} = e^{\hat {A}} e^{\hat {B}} e^{- \frac {1} {2} [ \hat {A} , \hat {B} ]}\label{1.19}\]
3. \[e^{\hat {A}} e^{\hat {B}} = e^{\hat {B}} e^{\hat {A}} e^{- [ \hat {B} , \hat {A} ]} \label{1.19B}\]

Operador de Evolución en el Tiempo

Dado que el TDSE es determinista y lineal en el tiempo, podemos definir un operador que describa la dinámica de la función de onda:

\[\psi (t) = \hat {U} \left( t , t _ {0} \right) \psi \left( t _ {0} \right) \label{1.20}\]

\(U\)es el propagador de tiempo u operador de evolución temporal que evoluciona el sistema cuántico en función del tiempo. Representa la solución a la ecuación de Schrödinger dependiente del tiempo. Para investigar su forma consideramos el TDSE para un hamiltoniano independiente del tiempo:

\[\frac {\partial} {\partial t} \psi ( \overline {r} , t ) + \frac {i \hat {H}} {\hbar} \psi ( \overline {r} , t ) = 0 \label{1.21}\]

Para resolver esto, definiremos un operador exponencial\(\hat {T} = \exp ( - i \hat {H} t / \hbar )\), el cual se define a través de su expansión en una serie Taylor:

\[ \begin{align} \hat {T} &= \exp ( - i \hat {H} t / \hbar ) \\[4pt] &= 1 - \frac {i \hat {H} t} {\hbar} + \frac {1} {2 !} \left( \frac {i \hat {H} t} {\hbar} \right)^{2} - \cdots \end{align} \label{1.22}\]

También se puede confirmar a partir de la expansión que\(\hat {T}^{- 1} = \exp ( i \hat {H} t / \hbar ),\) señalando que\(\hat{H}\) es hermitiano y se desplaza con\(\hat{T}\). Multiplicando la Ecuación\ ref {1.21} de la izquierda por\(\hat {T}^{- 1}\), podemos escribir

\[\frac {\partial} {\partial t} \left[ \exp \left( \frac {i \hat {H} t} {\hbar} \right) \psi ( \overline {r} , t ) \right] = 0 \label{1.23}\]

e integrando\(t _ {0} \rightarrow t\), obtenemos

\[\exp \left( \frac {i \hat {H} t} {\hbar} \right) \psi ( \overline {r} , t ) - \exp \left( \frac {i \hat {H} t _ {0}} {\hbar} \right) \psi \left( \overline {r} , t _ {0} \right) = 0 \label{1.24}\]

\[\psi ( \overline {r} , t ) = \exp \left( \frac {- i \hat {H} \left( t - t _ {0} \right)} {\hbar} \right) \psi \left( \overline {r} , t _ {0} \right) \label{1.25}\]

Entonces, comparando con la ecuación\ ref {1.20}, vemos que el propagador de tiempo es

\[\hat {U} \left( t , t _ {0} \right) = \exp \left( \frac {- i \hat {H} \left( t - t _ {0} \right)} {\hbar} \right) \label{1.26}\]

Para el hamiltoniano independiente del tiempo para el que conocemos los autoestados\(\phi_n\) y los valores propios\(E_n\), podemos expresarlo de una forma práctica usando la Ecuación\ ref {1.14}

\[\psi _ {n} ( \overline {r} , t ) = e^{- i E _ {n} \left( t - t _ {0} \right) / \hbar} \psi _ {n} \left( \overline {r} , t _ {0} \right) \label{1.27}\]

Alternativamente, si sustituimos el operador de proyección (o relación de identidad)

\[\sum _ {n} | \varphi _ {n} \rangle \langle \varphi _ {n} | = 1 \label{1.28}\]

en Ecuación\ ref {1.26}, vemos

\[\begin{align} \hat {U} \left( t , t _ {0} \right) &= e^{- i \hat {H} \left( t - t _ {0} \right) / \hbar} \sum _ {n} | \varphi _ {n} \rangle \langle \varphi _ {n} | \\[4pt] &= \sum _ {n} e^{- i \omega _ {n} \left( t - t _ {0} \right)} | \varphi _ {n} \rangle \langle \varphi _ {n} | \end{align}\]

\[\omega _ {n} = \frac {E _ {n}} {\hbar}\]

Así que ahora podemos escribir nuestra función de onda de desarrollo del tiempo como

\[\begin{align} | \psi _ {n} ( \overline {r} , t ) \rangle & = | \varphi _ {n} \rangle \sum _ {n} e^{- i \omega _ {n} \left( t - t _ {0} \right)} \left\langle \varphi _ {n} | \psi _ {n} \left( \overline {r} , t _ {0} \right) \right\rangle \\ & = \sum _ {n} e^{- i \omega _ {n} \left( t - t _ {0} \right)} c _ {n} \\ & = \sum _ {n} c _ {n} (t) | \varphi _ {n} \rangle \end{align} \label{1.30}\]

Como está escrito en la Ecuación\ ref {1.20}, vemos que el propagador del tiempo\(\hat {U} \left( t , t _ {0} \right)\), actúa hacia la derecha (sobre kets) para evolucionar el sistema en el tiempo. La evolución de las funciones de onda conjugadas (bras) se encuentra bajo el conjugado hermitiano de\(\hat {U} \left( t , t _ {0} \right)\), actuando a la izquierda:

\[\langle \psi (t) | = \langle \psi \left( t _ {0} \right) | \hat {U}^{\dagger} \left( t , t _ {0} \right) \label{1.31}\]

De su definición como expansión y reconociendo\(\hat{H}\) como hermitiano, se puede ver que

\[\hat {U}^{\dagger} \left( t , t _ {0} \right) = \exp \left[ \frac {i \hat {H} \left( t - t _ {0} \right)} {\hbar} \right] \label{1.32}\]

Señalando que\(\hat{U}\) es unitario,\(\hat {U}^{\dagger} = \hat {U}^{- 1}\), a menudo nos referimos\(\hat {U}^{\dagger}\) como el operador de inversión de tiempo.