4.1: Introducción a la dinámica disipativa

¿Cómo surge el comportamiento irreversible, un sello distintivo de los sistemas químicos, de la ecuación determinista de Schrödinger dependiente del tiempo? Responderemos a esta pregunta específicamente en el contexto de las transiciones cuánticas de un estado energético dado del sistema a estados energéticos de su entorno. Cualitativamente, se puede esperar que dicho comportamiento surja de la interferencia destructiva entre las soluciones oscilatorias del sistema y el conjunto de múltiples estados de energía estrechamente empaquetados del baño. Para ilustrar este punto, considere el siguiente cálculo para la amplitud de probabilidad para un estado inicial del sistema acoplado a un número finito pero creciente de estados elegidos aleatoriamente pertenecientes al baño.

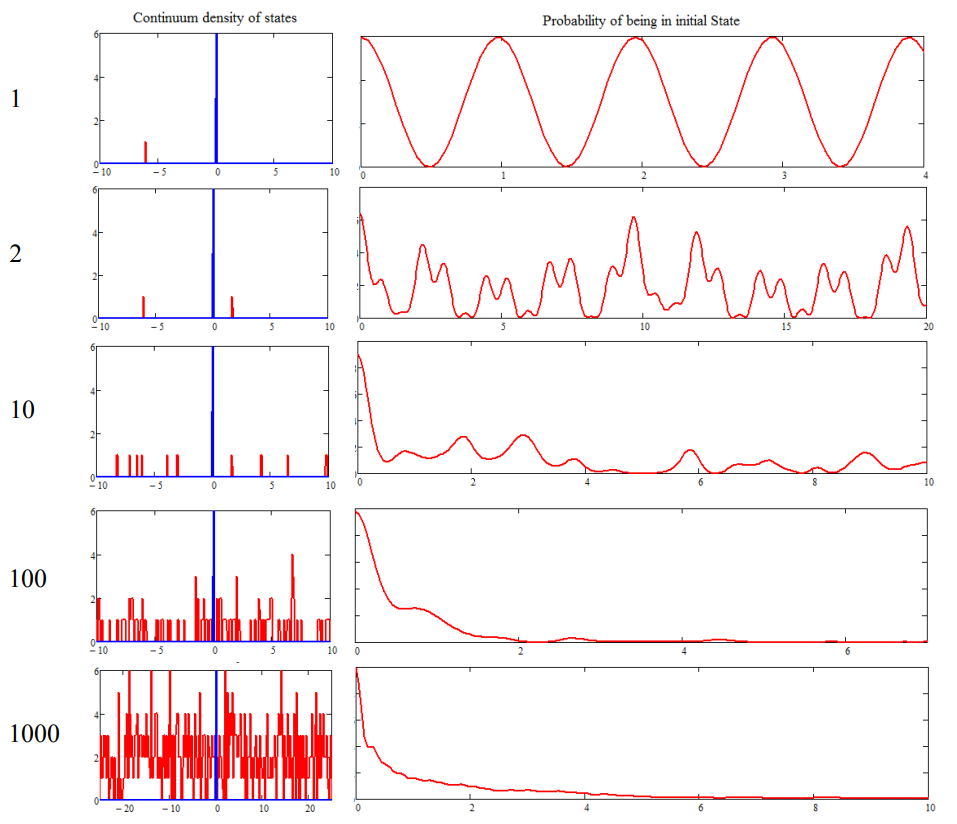
Aquí, incluso con solo 100 o 1000 estados, las recurrencias en la amplitud del estado inicial son suprimidas por la interferencia destructiva entre trayectorias. Claramente en el límite de que los estados aceptores son verdaderamente continuos, la amplitud inicial preparada en se\(\ell\) extenderá a través de un número infinito de estados continuos. Lo veremos más de cerca describiendo la relajación de un estado inicialmente preparado como resultado del acoplamiento a un continuo de estados del entorno. Esto es común a todos los procesos disipativos en los que el entorno al sistema de interés forman una banda continua de estados.

Para comenzar, definamos un continuum. Estamos familiarizados con las funciones propias caracterizadas por niveles de energía cuantificados, donde solo se permiten valores discretos de la energía. Sin embargo, este no es un requisito general. Los niveles discretos son característicos de las partículas en potenciales unidos, pero las partículas libres pueden tomar un rango continuo de energías dado por su impulso,

\[ E = \dfrac{\langle p^2 \rangle}{2m}.\]

Lo mismo se aplica a las superficies de energía potencial disociativa y a los potenciales ligados en los que la energía excede la energía de unión. Por ejemplo, la fotoionización o fotodisociación de una molécula implica un campo de luz que acopla un estado unido en un continuo. Otros ejemplos son comunes en la materia condensada. Los movimientos intermoleculares de un líquido, las vibraciones reticulares de un cristal o las energías permitidas dentro de la estructura de banda de un metal o semiconductor son ejemplos de un continuo.

Para un estado discreto embebido en tal continuo, la Regla de Oro da la probabilidad de transición del estado del sistema\(| \ell \rangle\) a un estado continuo\(| \ell \rangle\) como:

\[\overline {w} _ {k \ell} = \frac {\partial \overline {P} _ {k \ell}} {\partial t} = \frac {2 \pi} {\hbar} \left| V _ {k \ell} \right|^{2} \rho \left( E _ {k} = E _ {\ell} \right)\]

La velocidad de transición\(\overline {\mathcal {W}} _ {k \ell}\) es constante en el tiempo, cuando\(\left| V _ {k \ell} \right|^{2}\) es constante en el tiempo, lo que será cierto para intervalos de tiempo cortos. Bajo estas condiciones la integración de la ecuación de tasa de la izquierda da

\[\begin{align} \overline {P} _ {k \ell} &= \overline {w} _ {k \ell} \left( t - t _ {0} \right) \\[4pt] \overline {P} _ {\ell \ell} &= 1 - \overline {P} _ {k \ell}. \end{align}\]

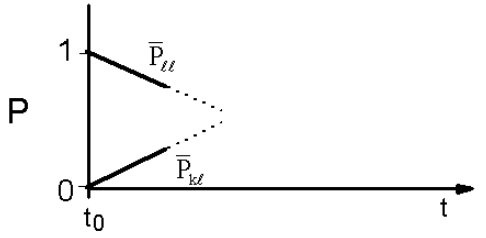
La probabilidad de transición al continuo de los estados de baño varía linealmente en el tiempo. Como señalamos, esto claramente sólo funcionará para tiempos tales que

\[P _ {k} (t) - P _ {k} ( 0 ) \gg1.\]

¿Qué comportamiento a largo plazo esperamos? Una tasa independiente del tiempo con población regida por

\[\overline {w} _ {k \ell} = \partial \overline {P} _ {k \ell} / \partial t\]

es un sello distintivo de cinética de primer orden y relajación exponencial. De hecho, para la relajación exponencial fuera de un estado\(\ell\), el comportamiento a corto plazo se parece al resultado de primer orden:

\[\begin{align} \overline {P} _ {\ell \ell} (t) &= \exp \left( - \overline {w} _ {k \ell} t \right) \\ &= 1 - \overline {w} _ {k \ell} t + \ldots\label{3.4} \end{align} \]

Entonces podríamos creer que\(\overline {\mathcal {W}} _ {k \ell}\) representa la tangente al comportamiento de relajación en\(t - 0\). El problema que teníamos anteriormente era que no teníamos en cuenta el agotamiento del estado inicial. De hecho, veremos que cuando miramos un toque más cuidadosamente, que el comportamiento de relajación a largo plazo del estado\(\ell\) es exponencial y se rige por la tasa de regla de oro. La decadencia del estado inicial es irreversible porque hay retroalimentación con una distribución de fases destructivamente interferentes.

Formulemos este problema un poco más cuidadosamente. Analizaremos las transiciones a un continuo de estados\(\{k \}\) desde un estado inicial\(\ell\) bajo una constante perturbación.

Estos juntos forman un conjunto completo; así que para

\[H (t) = H _ {0} + V (t)\]

con\(H _ {0} | n \rangle = E _ {n} | n \rangle\).

\[1 = \sum _ {n} | n \rangle \langle n | = | \ell \rangle \left\langle \ell \left| + \sum _ {k} \right| k \right\rangle \langle k | \label{3.5}\]

A medida que avanzamos, verá que podemos identificarnos\(\ell\) con el “sistema” y\(\{k \}\) con el “baño” cuando partimos

\[H _ {0} = H _ {S} + H _ {B}.\]

Ahora hagamos algunas suposiciones simplificadoras. Para las transiciones al continuum, asumiremos que las transiciones solo ocurren entre\(\ell\) y estados del continuum, pero que no hay interacciones entre estados del continuum:\(\left\langle k | V | k^{\prime} \right\rangle = 0\). Esto se puede racionalizar pensando en este problema como un conjunto discreto de estados que interactúan con un continuo de modos normales. Además, asumiremos que el acoplamiento de los estados inicial con el continuo es una constante para todos los estados\(k\):\(\langle \ell | V | k \rangle = \left\langle \ell | V | k^{\prime} \right\rangle = \cdots\). Por razones que veremos más adelante, también nos quedaremos con el elemento de matriz diagonal\(\langle \ell | V | \ell \rangle = 0\). Con estos supuestos, podemos resumir el hamiltoniano para nuestro problema como

\ begin {alineado}
H (t) &=H_ {0} +V (t)\\
H_ {0} &=|\ ell\ rangle E_ {\ ell}\ izquierda\ langle\ ell\ izquierda|+\ sum_ {k}\ derecha| k\ derecha\ rangle E_ {k}\ langle k|\\
V (t) &=\ sum_ {k}\ izquierda [|k\ rangle V_ {k\ ell}\ langle\ ell|+|\ ell\ rangle V_ {2 k}\ langle k|\ derecha] +|\ ell\ rangle V_ {\ ell\ ell }\ langle\ ell|
\ etiqueta {3.6}\ final {alineado}

Buscamos una descripción más precisa de la ocupación de los estados inicial y continuo, para lo cual utilizaremos los coeficientes de expansión de imagen de interacción

\[b _ {k} (t) = \left\langle k \left| U _ {I} \left( t , t _ {0} \right) \right| \ell \right\rangle \label{3.7}\]

Anteriormente, vimos que la solución exacta a\(U_I\) era:

\[U _ {I} \left( t , t _ {0} \right) = 1 - \frac {i} {\hbar} \int _ {t _ {0}}^{t} d \tau V _ {I} ( \tau ) U _ {I} \left( \tau , t _ {0} \right) \label{3.8}\]

Esta forma no era muy práctica, ya que\(U_I\) es una función de sí misma. Para la teoría de perturbación de primer orden, establecemos el término final en esta ecuación\(U_I\),\(U _ {I} \left( \tau , t _ {0} \right) \rightarrow 1\). Aquí, para mantener la retroalimentación entre\( |\ell \rangle \) y los estados del continuo, la mantenemos tal cual.

\[b _ {k} (t) = \langle k | \ell \rangle - \frac {i} {\hbar} \int _ {t _ {0}}^{t} d \tau \left\langle k \left| V _ {I} ( \tau ) U _ {I} \left( \tau , t _ {0} \right) \right| \ell \right\rangle \label{3.9}\]

Insertando la ecuación\ ref {3.7}, y reconociendo\(k \neq l\),

\[b _ {k} (t) = - \frac {i} {\hbar} \sum _ {n} \int _ {t _ {0}}^{t} d \tau e^{i \omega _ {h n} \tau} V _ {k n} b _ {n} ( \tau ) \label{3.10}\]

Tenga en cuenta, no\(V_{kn}\) es una función del tiempo. La ecuación\ ref {3.10} expresa la ocupación de estado\(k\) en términos de la historia completa del sistema a partir\(t _ {0} \rightarrow t\) de la amplitud fluyendo de un lado a otro entre los estados n. La ecuación\ ref {3.10} es solo la forma integral de las ecuaciones diferenciales acopladas que usamos antes:

\[i \hbar \frac {\partial b _ {k}} {\partial t} = \sum _ {n} e^{i \omega _ {b n} t} V _ {k n} b _ {n} (t) \label{3.11}\]

Estas formas exactas permiten la retroalimentación entre todos los estados, en los que las amplitudes\(b_k\) dependen de todos los demás estados. Dado que solo\(\ell\) se alimenta de a\(k\), podemos eliminar la suma en la Ecuación\ ref {3.10} y expresar la amplitud compleja de un estado dentro del continuum como

\[b _ {k} = - \frac {i} {\hbar} V _ {k \ell} \int _ {t _ {0}}^{t} d \tau e^{i \omega _ {k} \tau} b _ {\ell} ( \tau ) \label{3.12}\]

Queremos calcular la tasa de salida\(| \ell \rangle\), incluyendo la alimentación desde el continuo de regreso al estado inicial. De la Ecuación\ ref {3.11} podemos separar términos que involucran el continuo y el estado inicial:

\[i \hbar \frac {\partial} {\partial t} b _ {\ell} = \sum _ {k \neq \ell} e^{i \omega _ {\mu} t} V _ {\ell k} b _ {k} + V _ {\ell \ell} b _ {\ell} \label{3.13}\]

Ahora sustituyendo la Ecuación\ ref {3.12} en Ecuación\ ref {3.13}, y estableciendo\(t_0 =0\):

\[\frac {\partial b _ {\ell}} {\partial t} = - \frac {1} {\hbar^{2}} \sum _ {k \neq \ell} \left| V _ {k \ell} \right|^{2} \int _ {0}^{t} b _ {\ell} ( \tau ) e^{i \omega _ {k} ( \tau - t )} d \tau - \frac {i} {\hbar} V _ {\ell \ell} b _ {\ell} (t) \label{3.14}\]

Esta es una ecuación integro-diferencial que describe cómo el desarrollo del tiempo\(b_ℓ\) depende de toda la historia del sistema. Tenga en cuenta que tenemos dos variables de tiempo para las dos rutas de propagación:

\[\left. \begin{array} {l} {\tau : | \ell \rangle \rightarrow | k \rangle} \\ {t : | k \rangle \rightarrow | \ell \rangle} \end{array} \right. \label{3.15}\]

El siguiente supuesto es que\(b_ℓ\) varía lentamente en relación con\(\omega_{kℓ}\), por lo que podemos eliminarlo de integral. Esta es efectivamente una declaración de acoplamiento débil:\(\hbar \omega _ {k \ell} \gg V _ {k \ell}\). \(b\)es una función del tiempo, pero como está en el cuadro de interacción evoluciona lentamente en comparación con las\(\omega_{kℓ}\) oscilaciones en la integral.

\[\frac {\partial b _ {\ell}} {\partial t} = b _ {\ell} \left[ - \frac {1} {\hbar^{2}} \sum _ {k \neq \ell} \left| V _ {k \ell} \right|^{2} \int _ {0}^{t} e^{i \omega _ {k} ( \tau - t )} d \tau - \frac {i} {\hbar} V _ {\ell \ell} \right] \label{3.16}\]

Ahora, queremos la evolución a largo plazo de\(b\), por tiempos\(\omega _ {k \ell} t > > 1\), investigaremos el límite de integración\(t \rightarrow \infty\).

Nota

Integración compleja de la Ecuación\ ref {3.16}: Definición\(t^{\prime} = \tau - t\)

\[\int _ {0}^{t} e^{i \omega _ {k l} ( \tau - t )} d \tau = - \int _ {0}^{t} e^{i \omega _ {k l} t^{\prime}} d t^{\prime} \label{3.17}\]

La integral\(\lim _ {T \rightarrow \infty} \int _ {0}^{T} e^{i \omega t^{\prime}} d t^{\prime}\) es puramente oscilatoria y no se comporta bien. La estrategia para resolver esto es integrar:

\[\begin{align} \lim _ {\varepsilon \rightarrow 0^{+}} \int _ {0}^{\infty} e^{( i \omega + \varepsilon ) t^{\prime}} d t^{\prime} & = \lim _ {\varepsilon \rightarrow 0^{+}} \frac {1} {i \omega + \varepsilon} \\ & = \lim _ {\varepsilon \rightarrow 0^{+}} \left( \frac {\varepsilon} {\omega^{2} + \varepsilon^{2}} + i \frac {\omega} {\omega^{2} + \varepsilon^{2}} \right) \\ & = \pi \delta ( \omega ) - i \mathbb {P} \frac {1} {\omega} \label{3.19} \end{align}\]

(Esta expresión es válida cuando se usa bajo una integral) En el término final hemos escrito en términos de la Parte Principio de Cauchy:

\[\mathbb {P} \left( \frac {1} {x} \right) = \left\{\begin{array} {l l} {\frac {1} {x}} & {x \neq 0} \\ {0} & {x = 0} \end{array} \right. \label{3.20}\]

Usando la ecuación\ ref {3.19}, la ecuación\ ref {3.16} se convierte en\ ref {3.21}

\[\frac {\partial b _ {\ell}} {\partial t} = b _ {\ell} [ - \underbrace {\frac {\pi} {\hbar^{2}} \sum _ {k \neq \ell} \left| V _ {k \ell} \right|^{2} \delta \left( \omega _ {k \ell} \right)} _ {\text {term} 1} - \frac {i} {\hbar} \left( \underbrace {V _ {\ell \ell} + \mathbb {P} \sum _ {k \neq \ell} \frac {\left| V _ {k \ell} \right|^{2}} {E _ {k} - E _ {\ell}} )} _ {\text {term} 2} \right] \label{3.21}\]

Tenga en cuenta que el Término 1 es solo la tasa de la Regla de Oro, escrita explícitamente como una suma sobre estados continuos en lugar de una integral

\[\sum _ {k \neq \ell} \delta \left( \omega _ {k \ell} \right) \Rightarrow \hbar \rho \left( E _ {k} = E _ {\ell} \right) \label{3.22}\]

\[\overline {w} _ {k \ell} = \int d E _ {k} \rho \left( E _ {k} \right) \left[ \frac {2 \pi} {\hbar} \left| V _ {k l} \right|^{2} \delta \left( E _ {k} - E _ {\ell} \right) \right] \label{3.23}\]

Término 2 es solo la corrección de la energía de la teoría\(E_ℓ\) de perturbación independiente del tiempo de segundo orden,

\[\Delta E _ {\ell} = \langle \ell | V | \ell \rangle + \sum _ {k \neq l} \frac {\langle k | V | \left. \ell \right|^{2}} {E _ {k} - E _ {\ell}} \label{3.25} \]

Entonces, la evolución temporal de\(b _ {\ell}\) se rige por una simple ecuación diferencial de primer orden

\[\frac{\partial b_{\ell}}{\partial t}=b_{\ell}\left(-\frac{\bar{w}_{k \ell}}{2}-\frac{i}{\hbar} \Delta E_{\ell}\right)\]

Que se puede resolver con\(b _ {\ell} ( 0 ) = 1\) para dar

\[b _ {\ell} (t) = \exp \left( - \frac {\overline {w} _ {k l} t} {2} - \frac {i} {\hbar} \Delta E _ {\ell} t \right) \label{3.26}\]

Vemos que uno tiene decaimiento exponencial de amplitud de\(b _ {\ell}\)! Esta es una manera de relajación irreversible del acoplamiento al continuo. Ahora, dado que puede haber interferencias adicionales entre rutas, cambiamos de la imagen de interacción de nuevo a Schrödinger Picture,

\[c _ {\ell} (t) = \exp \left[ - \left( \frac {\overline {w} _ {k \ell}} {2} + i \frac {E _ {\ell}^{\prime}} {\hbar} \right) t \right] \label{3.27}\]

con la energía corregida

\[E _ {\ell}^{\prime} \equiv E _ {\ell} + \Delta E \label{3.28}\]

y

\[P _ {\ell} = \left| c _ {\ell} \right|^{2} = \exp \left[ - \overline {w} _ {k \ell} t \right] \label{3.29}\]

Se espera que las soluciones a la Ecuación de Schrödinger Dependiente del Tiempo sean complejas y oscilatorias. Lo que vemos aquí es un componente disipativo real y un componente dispersivo imaginario. La probabilidad decae exponencialmente desde el estado inicial. ¡La tasa de la Regla de Oro de Fermi te habla de largos tiempos!

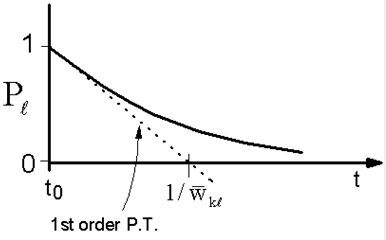
Ahora bien, ¿cuál es la probabilidad de aparecer en alguno de los estados\(|k \rangle\)? Usando la ecuación\ ref {3.12}:

\[b _ {k} (t) = - \frac {i} {\hbar} \int _ {0}^{t} V _ {k \ell} e^{i \omega _ {k l} \tau} b _ {\ell} ( \tau ) d \tau\]

\[= V _ {k \ell} \frac {1 - \exp \left( - \frac {\overline {w} _ {k \ell}} {2} t - \frac {i} {h} \left( E _ {\ell}^{\prime} - E _ {k} \right) t \right)} {E _ {k} - E _ {\ell}^{\prime} + i \hbar \overline {w} _ {k \ell} / 2}\]

\[= V _ {k \ell} \frac {1 - c _ {\ell} (t)} {E _ {k} - E _ {\ell}^{\prime} + i \hbar \overline {w} _ {k \ell} / 2}\]

(3.30) Si investigamos el límite de tiempo largo (\(t \rightarrow \infty\)), señalando que\(P _ {k \ell} = \left| b _ {k} \right|^{2}\), encontramos

\[P _ {k l} = \frac {\left| V _ {k l} \right|^{2}} {\left( E _ {k} - E _ {i}^{\prime} \right)^{2} + \Gamma^{2} / 4} \label{3.31}\]

con

\[\Gamma \equiv \overline {w} _ {k \ell} \cdot \hbar \label{3.32}\]

La distribución de probabilidad para los estados de ocupación dentro del continuo es descrita por una distribución lorentziana con probabilidad máxima centrada en la energía corregida del estado inicial\(E _ {\ell}^{\prime}\). El ancho de la distribución viene dado por la tasa de relajación, que es proxy para\(\left| V _ {k \ell} \right|^{2} \rho \left( E _ {\ell} \right)\), el acoplamiento al continuum y densidad de estados.

Lecturas

1. Cohen-Tannoudji, C.; Diu, B.; Lalöe, F., Mecánica Cuántica. Wiley-Interscience: París, 1977; p. 1344.
2. Merzbacher, E., Mecánica Cuántica. 3a ed.; Wiley: Nueva York, 1998; p. 510.
3. Nitzan, A., Dinámica Química en Fases Condensadas. Oxford University Press: Nueva York, 2006; p. 305. 4. Schatz, G. C.; Ratner, M. A., Mecánica Cuántica en Química. Publicaciones de Dover: Mineola, NY, 2002; Ch. 9.