8.1: Estados mixtos

Conceptualmente ahora estamos cambiando de marcha para desarrollar herramientas y formas de pensar sobre los problemas de fase condensada. Lo que hemos discutido hasta ahora son las propiedades dependientes del tiempo de los estados puros, los estados de un sistema cuántico que puede caracterizarse por una sola función de onda. Para estados puros se puede escribir precisamente el hamiltoniano para todas las partículas y campos en el sistema de interés. Se trata de sistemas que están aislados de su entorno, o sistemas aislados a los que introducimos un potencial dependiente del tiempo. Para describir problemas en fases condensadas, las cosas son diferentes. Las moléculas en medios densos interactúan entre sí, y como resultado no hay dos moléculas que tengan el mismo estado. La energía colocada en un grado de libertad finalmente se filtrará irreversiblemente en su entorno. No podemos escribir un hamiltoniano exacto para estos problemas; sin embargo, podemos concentrarnos en unos pocos grados de libertad que se observan en una medición, e intentar describir la influencia del entorno de manera estadística.

Estas observaciones llevan al concepto de estados mixtos o mezclas estadísticas. Un estado mixto se refiere a cualquier caso en el que describimos el comportamiento de un conjunto para el cual inicialmente no existe una relación de fase entre los elementos de la mezcla. Los ejemplos incluyen un sistema en equilibrio térmico y estados preparados independientemente. Para estados mixtos tenemos información imperfecta sobre el sistema, y utilizamos promedios estadísticos para describir observables cuánticos.

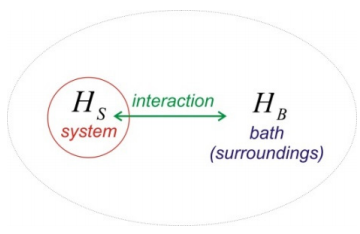
¿Cómo entra un sistema en un estado mixto? Generalmente, si tienes dos sistemas y los pones en contacto entre sí, la interacción entre ambos conducirá a un nuevo sistema que es inseparable. Considerar dos sistemas\(H_S\) y\(H_B\) para los cuales los autoestados de\(H_S\) son\(| n \rangle\) y los de\(H_B\) son\(| \alpha \rangle\).

\[H _ {0} = H _ {S} + H _ {B}\]

\[\left. \begin{array} {l} {H _ {S} | n \rangle = E _ {n} | n \rangle} \\ {H _ {B} | \alpha \rangle = E _ {\alpha} | \alpha \rangle} \end{array} \right. \label{0.2}\]

Antes de que estos sistemas interactúen, el estado del sistema\(| \psi _ {0} \rangle\) puede describirse como estados de producto de\(| n \rangle\) y\(| \alpha \rangle\).

\[| \psi _ {0} \rangle = | \psi _ {S}^{0} \rangle | \psi _ {B}^{0} \rangle \label{0.3}\]

\[| \psi _ {S}^{0} \rangle = \sum _ {n} s _ {n} | n \rangle\]

\[| \psi _ {B}^{0} \rangle = \sum _ {\alpha} b _ {\alpha} | \alpha \rangle\]

\[| \psi _ {0} \rangle = \sum _ {n , \alpha} s _ {n} b _ {\alpha} | n \alpha \rangle\]

donde\(s\) y\(b\) son coeficientes de expansión. Después de que se permita que estos estados interactúen, tenemos un nuevo estado\(| \psi (t) \rangle\). El nuevo estado aún puede expresarse en la base de orden cero, aunque esto no representa los autoestados del nuevo hamiltoniano:

\[H = H _ {0} + V \label{0.6}\]

\[| \psi (t) \rangle = \sum _ {n , \alpha} c _ {n , \alpha} | n \alpha \rangle \label{0.7}\]

Para cualquier punto en el tiempo,\(C _ {n , \alpha}\) es la amplitud compleja para el\(| n \alpha \rangle\) estado mixto. En términos generales, en cualquier momento después de poner en contacto los sistemas\(c _ {n , \alpha} \neq s _ {n} b _ {a}.\). El coeficiente n,\(c_{n, \alpha}\) codifica\(P _ {n , \alpha} = \left| c _ {n , \alpha} \right|^{2}\), la probabilidad conjunta para encontrar partícula de\(\left|\psi_{S}\right\rangle \text {in state}|n\rangle\) y simultáneamente encontrar partícula de\(\left|\psi_{B}\right\rangle \text {in state}|\alpha\rangle\). En el caso de observables experimentales, normalmente somos capaces de realizar mediciones en el sistema HS, y somos ciegos a HB. Entonces nos interesa la probabilidad de ocupar un estado propio particular del sistema promediado sobre los grados de libertad del baño:

\[P _ {n} = \sum _ {\alpha} P _ {n , \alpha} = \sum _ {\alpha} \left| c _ {n , \alpha} \right|^{2} = \left\langle \left| c _ {n} \right|^{2} \right\rangle \label{0.8}\]

Ahora veamos el pensamiento que implica describir conjuntos. Imagine una solución a temperatura ambiente de moléculas disueltas en un disolvente. Las mismas funciones moleculares hamiltonianas y onduladas se pueden utilizar para expresar el estado de cualquier molécula en el conjunto. Sin embargo, los detalles de las amplitudes de los autoestados en cualquier momento también dependerán del entorno local dependiente del tiempo.

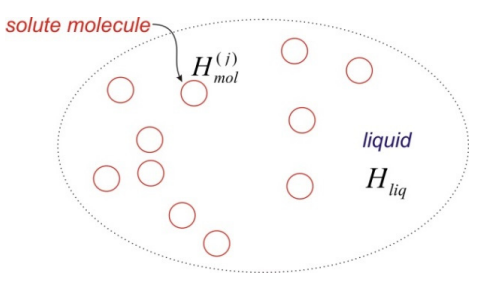
Describiremos este problema con la ayuda de un hamiltoniano molecular\(H_{m o l}^{(j)}\), que describe el estado de la molécula j dentro de la solución a través de la función de onda\(\left|\psi^{(j)}\right\rangle\). También tenemos un hamiltoniano para el líquido\(H_{l i q}\) en el que envolvemos todos los grados de libertad solvente. El Hamiltoniano completo para la solución se puede expresar en términos de una suma sobre las moléculas de soluto N y el líquido, las interacciones entre las moléculas\(H_{i n t}\) de soluto y cualquier interacción soluto-disolvente\(H_{mol-liq}\):

\[\overline {H} = \sum _ {j = 1}^{N} H _ {m o l}^{( j )} + H _ {l i q} + \sum _ {j , k = 1 \atop j > k}^{N} H _ {\text {int}}^{( j , k )} + \sum _ {j = 1}^{N} H _ {m o l - l i q}^{( j )} \label{0.9}\]

Para nuestros propósitos, tomamos el Hamiltoniano molecular como el mismo para todas las moléculas de soluto, es decir,\(H_{m o l}^{(j)}=H_{m o l}\) que obedece a un TISE

\[H _ {m o l} | \psi _ {n} \rangle = E _ {n} | \psi _ {n} \rangle \label{0.10}\]

Expresaremos el estado de cada molécula en esta molécula aislada de base propia. Por las circunstancias que nos preocupan, donde no hay interacciones o correlaciones entre moléculas de soluto, se nos permite descuidar\(H_{int}\). Implícito en esta afirmación es que creemos que no existe una relación de fase mecánica cuántica entre las diferentes moléculas de soluto. También bajaremos\(H_{liq}\), ya que no es el foco de nuestros intereses y no influirá en las conclusiones. Por lo tanto, podemos escribir el hamiltoniano para cualquier molécula individual como

\[H^{( j )} = H _ {m o l} + H _ {m o l - l i q}^{( j )} \label{0.11}\]

y el promedio estadístico hamiltoniano

\[\overline {H} = \frac {1} {N} \sum _ {j = 1}^{N} H^{( j )} = H _ {m o l} + \left\langle H _ {m o l - l i q} \right\rangle \label{0.12}\]

Este hamiltoniano refleja un promedio conjunto del hamiltoniano molecular bajo la influencia de una interacción soluto-disolvente variable. Para describir el estado de cualquier molécula en particular, podemos definir una función de onda molecular\(\left|\psi_{n}^{(j)}\right\rangle\), que expresamos como una expansión en los autoestados moleculares aislados,

\[| \psi _ {n}^{( j )} \rangle = \sum _ {n} c _ {n}^{( j )} | \psi _ {n} \rangle \label{0.13}\]

Aquí los coeficientes de expansión varían según la molécula debido a su interacción con el líquido, pero todos se expresan en términos de los propios estados de moléculas aisladas. Obsérvese que esta expansión es en esencia la misma que la Ecuación\ ref {0.7}, con la asociación\(c _ {n}^{( j )} \Leftrightarrow c _ {n , \alpha}\). En cualquier caso, el estado mixto surge de diversas interacciones con el medio ambiente. Estos pueden ser estáticos y aparecer a partir del promedio del conjunto, o dependientes del tiempo y surgir de fluctuaciones en el entorno. Reconociendo la independencia de diferentes moléculas, la función de onda para el sistema completo se\(|\Psi\rangle\) puede expresar en términos de las funciones de onda para las moléculas individuales bajo la influencia de su entorno local\(\left|\psi^{(j)}\right\rangle\):

\[\overline {H} | \Psi \rangle = \overline {E} | \Psi \rangle \label{0.14}\]

\[| \Psi \rangle = | \psi^{( 1 )} \psi^{( 2 )} \psi^{( 3 )} \cdots \rangle = \prod _ {j = 1}^{N} | \psi^{( j )} \rangle \label{0.15}\]

\[\overline {E} = \sum _ {j = 1}^{N} E^{( j )} \label{0.16}\]

Ahora nos volvemos la atención a los valores de expectativa que mediríamos en un experimento. Primero reconocemos que para la molécula individual j, se expresaría el valor de expectativa para un operador interno

\[\left\langle A^{( j )} \right\rangle = \left\langle \psi^{( j )} \left| \hat {A} \left( p _ {j} , q _ {j} \right) \right| \psi^{( j )} \right\rangle \label{0.17}\]

Esta cantidad puramente mecánica cuántica es en sí misma un promedio. Representa el valor medio obtenido para un gran número de mediciones realizadas en un sistema preparado idénticamente, y refleja la necesidad de promediar sobre las incertidumbres cuánticas intrínsecas en la posición y momento de las partículas. En el caso de un estado mixto, también debemos promediar el valor de expectativa sobre el conjunto de diferentes moléculas. En el caso de nuestra solución, esto implicaría un promedio del valor de expectativa sobre las moléculas de N.

\[\langle \langle A \rangle \rangle = \frac {1} {N} \sum _ {j = 1}^{N} \left\langle A^{( j )} \right\rangle \label{0.18}\]

Aquí se escriben corchetes dobles para enfatizar que conceptualmente hay dos niveles de estadística en este promedio. El primero involucra la incertidumbre sobre las mediciones de la misma molécula en el estado puro idéntico, mientras que el segundo es un promedio sobre las variaciones del estado del sistema dentro de un conjunto. Sin embargo, bajaremos esta notación cuando estemos tratando con conjuntos, y tomaremos como entendido que los valores de expectativa deben promediarse sobre una distribución. Ampliar la Ecuación\ ref {0.18} con el uso de Ecuaciones\ ref {0.13} y\ ref {0.17} nos permite escribir

\[\langle A \rangle = \frac {1} {N} \sum _ {n , m} \sum _ {j = 1}^{N} c _ {m}^{( j )} \left( c _ {n}^{( j )} \right)^{*} \left\langle \psi _ {n} | \hat {A} | \psi _ {m} \right\rangle \label{0.19}\]

El segundo término simplifica la primera expresión al realizar un promedio de conjunto sobre las amplitudes complejas de función de onda. Utilizamos esta expresión para escribir una matriz de densidad u operador de densidad\(\rho\), cuyos elementos matriciales son

\[\rho _ {m n} = \left\langle c _ {m} c _ {n}^{*} \right\rangle \label{0.20}\]

Entonces el valor de expectativa se convierte

\[\left.\begin{aligned} \langle A \rangle & = \sum _ {n , m} \rho _ {m n} A _ {n m} \\ & = \operatorname {Tr} ( \rho \hat {A} ) \end{aligned} \right. \label{0.21}\]

Aquí la traza\(Tr[...]\) se refiere a una traza sobre los elementos diagonales de la matriz\(\sum_{a}\langle a|\cdots| a\rangle\). Aunque estas matrices se evaluaron en base a los autoestados moleculares, enfatizamos que la definición y evaluación de la matriz de densidad y los elementos de la matriz operadora no son específicos de un conjunto de bases en particular.

Si bien este es solo un ejemplo, los principios son bastante generalmente a estados mixtos en la fase condensada. La función de onda es una cantidad que pretende describir un objeto molecular o nanoescala. En la medida en que la temperatura finita, las fluctuaciones, el desorden y la separación espacial aseguran que las relaciones de fase se aleatorizan entre diferentes nano-ambientes, se pueden caracterizar las propiedades moleculares de las fases condensadas como estados mixtos en los que se usa el promedio de conjunto para describir el interacciones de estos ambientes moleculares con su entorno.

El nombre matriz de densidad deriva de la observación de que desempeña el papel cuántico de una densidad de probabilidad. Comparando la Ecuación\ ref {0.21} con la determinación estadística del valor medio de\(A\),

\[\langle A \rangle = \sum _ {i = 1}^{M} P \left( A _ {i} \right) A _ {i} \label{0.22}\]

vemos que\(\rho\) juega el papel de la función de distribución de probabilidad\(P(A)\). Dado que\(\rho\) es hermitiano, se puede diagonalizar, y en esta base diagonal los elementos de la matriz de densidad son de hecho los pesos estadísticos o probabilidades de ocupar un estado dado del sistema.

Volviendo a nuestro ejemplo, y comparar la Ecuación\ ref {0.22} con la Ecuación\ ref {0.18} también implica eso\(P_i(A) = 1/N\), es decir, que la contribución de cada molécula al promedio es estadísticamente equivalente. Obsérvese también que el estado del sistema descrito por la Ecuación\ ref {0.15} es un sistema de energía fija. Entonces, la densidad de probabilidad en la Ecuación\ ref {0.18} indica que esta expresión se aplica a un conjunto microcanónico (\(N\)\(V\),,\(E\)) en el que cualquier realización de un sistema a energía fija es igualmente probable, y el peso estadístico es el inverso del número de microestados: \(P=1 / \Omega\). En el caso de un sistema en contacto con un baño de calor con temperatura T, es decir, el conjunto canónico (N, V, T) expresamos ahora el promedio en términos de la probabilidad de que un miembro de un conjunto con energía promedio fija pueda acceder a un estado de energía\(E\).