9.1: Conceptos y definiciones

Como un cambio en nuestro pensamiento, ahora tenemos que preocuparnos por los conjuntos. Muy a menudo, nos ocuparemos de sistemas en un estado de equilibrio con una temperatura fija para la cual muchos estados cuánticos son accesibles para el sistema. Para comparar los cálculos de estados cuánticos puros con observables experimentales en muestras macroscópicas, asumimos que todas las moléculas han sido preparadas y observadas de la misma manera, de manera que los valores de expectativa cuántica para los operadores internos pueden compararse directamente con observaciones experimentales. Para los estados mixtos, hemos visto la necesidad de realizar una capa adicional de promediación sobre el conjunto en el cálculo de los valores de expectativa.

Quizás el cambio más significativo entre los estados aislados y la materia condensada es la dinámica. De la ecuación de Schrödinger dependiente del tiempo, vemos que las leyes que rigen la evolución temporal de los sistemas mecánicos cuánticos aislados son invariantes bajo inversión temporal. Es decir, no hay direccionalidad intrínseca al tiempo. Si uno invierte el signo del tiempo y con ello momenta de objetos, deberíamos ser capaces de revertir exactamente el movimiento y propagar el sistema a donde estaba en un momento anterior. Este es también el caso de los sistemas clásicos que evolucionan bajo la ecuación de movimiento de Newton. Por el contrario, cuando un sistema cuántico está en contacto con otro sistema que tiene muchos grados de libertad, emerge una dirección definida para el tiempo, “la flecha del tiempo”, y la dinámica del sistema ya no es reversible. En tales sistemas irreversibles un estado preparado bien definido decae en el tiempo a un estado de equilibrio donde la energía se ha disipado y las relaciones de fase se pierden entre los diversos grados de libertad.

Adicionalmente, los sistemas de fase condensada en un local, escala microscópica todos tienen un grado de aleatoriedad o ruido a su dinámica que representan fluctuaciones locales en la energía en la escala de\(k _ {B} T\). Este comportamiento se observa incluso a través de las ecuaciones de movimiento que rigen la dinámica son deterministas. ¿Por qué? Es porque generalmente tenemos un conocimiento imperfecto sobre todos los grados de libertad que influyen en el sistema, o vemos experimentalmente su comportamiento a través de una perspectiva altamente restringida. Por ejemplo, es común en experimentos observar el comportamiento de las fases condensadas a través de una sonda molecular incrustada dentro o bajo la influencia de su entorno. Las propiedades físicas de la sonda se entrelazan con la dinámica del medio circundante, y para nosotros esto aparece como comportamiento aleatorio, por ejemplo como movimiento browniano. Otros ejemplos de la aparición de aleatoriedad a partir de ecuaciones deterministas de movimiento incluyen patrones climáticos, mercados financieros y evolución biológica. Entonces, ¿cómo surgen el comportamiento irreversible y las fluctuaciones aleatorias, señas de identidad de todos los sistemas químicos, de la ecuación determinista de Schrödinger dependiente del tiempo? Esta fascinante pregunta será el tema central en nuestros esfuerzos en el futuro.

Definiciones

Empecemos por establecer algunas definiciones y lenguaje que nos serán útiles. Primero clasificamos los sistemas químicos de interés como sistemas de equilibrio o no equilibrio. Un sistema de equilibrio es aquel en el que las propiedades macroscópicas (es decir, las variables intensivas) son invariantes con el tiempo, o al menos invariantes en las escalas de tiempo sobre las cuales se ejecuta experimentos y se observa el sistema. Además, no hay concentraciones de estado estacionario ni gradientes de energía (corrientes) en el sistema. Aunque son macroscópicamente invariantes, los estados de equilibrio son microscópicamente dinámicos.

Para sistemas en equilibrio térmico describiremos su comportamiento dependiente del tiempo como dinámicamente reversible o irreversible. Para nosotros, reversible significará que un sistema evoluciona determinísticamente. El conocimiento del estado del sistema en un punto en el tiempo y la ecuación de movimiento significa que se puede describir el estado del sistema para todos los puntos en el tiempo posteriores o previamente. Los sistemas irreversibles no son deterministas. Es decir, el conocimiento del estado del sistema en un momento dado no proporciona suficiente información para determinar con precisión su estado pasado.

Dado que todos los estados son irreversibles en el sentido más estricto, la distinción suele estar relacionada con la escala de tiempo de observación. Para un sistema dado, en una escala de tiempo suficientemente corta la dinámica aparecerá determinista mientras que en tiempos muy largos aparecerá aleatoria. Por ejemplo, la dinámica de un gas diluido parece balística en escalas de tiempo cortas en comparación con el tiempo medio de colisión entre partículas, mientras que su movimiento aparece aleatorio y difusivo en escalas de tiempo mucho más largas. La memoria se refiere a la capacidad de mantener el movimiento determinista y la reversibilidad, y cuantificaremos la decadencia de la memoria en el sistema con funciones de correlación. Para el caso de la dinámica cuántica, estamos particularmente interesados en las relaciones de fase entre grados cuánticos de libertad que resultan del movimiento determinista bajo la ecuación de Schrödinger dependiente del tiempo.

Los estados de no equilibrio se refiere a sistemas abiertos o cerrados sobre los que se ha actuado externamente, moviéndolos del equilibrio cambiando la población o energía de los estados cuánticos disponibles para el sistema. Termodinámicamente, el trabajo se realiza en el sistema, conduciendo a un gradiente de energía libre que el sistema de no equilibrio minimizará a medida que se reequilibra. Para los estados de no equilibrio, nos interesarán los procesos de relajación, que se refieren a los procesos dependientes del tiempo involucrados en el reequilibrio del sistema. La disipación se refiere a los procesos de relajación que implican la redistribución de energía como un estado de no equilibrio regresa hacia una distribución térmica. Sin embargo, existen otros procesos de relajación como la aleatorización de la orientación de un sistema alineado o la aleatorización de fase de oscilaciones sincronizadas.

Estadísticas

Con la necesidad de describir conjuntos, se utilizarán descripciones estadísticas de las propiedades y el comportamiento de un sistema. La variable\(A\), que puede ser una variable interna clásica o un operador cuántico, puede describirse estadísticamente en términos de los valores medios y medios cuadrados de\(A\) determinados a partir de un gran número de mediciones:

\[\langle A \rangle = \frac {1} {N} \sum _ {i = 1}^{N} A _ {i} \label{8.1}\]

\[\left\langle A^{2} \right\rangle = \frac {1} {N} \sum _ {i = 1}^{N} A _ {i}^{2} \label{8.2}\]

Aquí, la suma sobre\(i\) se refiere al promedio sobre mediciones\(N\) independientes. Alternativamente, estas ecuaciones se pueden expresar como

\[\langle A \rangle = \sum _ {n = 1}^{M} P _ {n} A _ {n} \label{8.3}\]

\[\left\langle A^{2} \right\rangle = \sum _ {n = 1}^{M} P _ {n} A _ {n}^{2} \label{8.4}\]

La suma sobre\(n\) se refiere a una suma sobre los valores\(M\) posibles que\(A\) puede tomar, ponderada por\(P_n\), la probabilidad de observar un valor particular\(A_n\). Cuando los valores accesibles provienen de una distribución continua en contraposición a discreta, se pueden describir las estadísticas en términos de los momentos de la función de distribución\(P(A)\),, que caracteriza la probabilidad de observar\(A\) entre\(A\) y\(A+dA\)

\[\langle A \rangle = \int d A A P ( A ) \label{8.5}\]

\[\left\langle A^{2} \right\rangle = \int d A A^{2} P ( A ) \label{8.6}\]

Para procesos dependientes del tiempo, reconocemos que es posible que estas distribuciones de probabilidad lleven una dependencia del tiempo,\(P(A,t)\). La capacidad de especificar un valor para\(A\) se captura en la varianza de la distribución

\[\sigma^{2} = \left\langle A^{2} \right\rangle - \langle A \rangle^{2} \label{8.7}\]

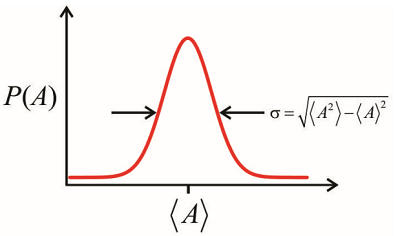
Aplicaremos promedios sobre distribuciones de probabilidad a la descripción de conjuntos de moléculas; sin embargo, debemos enfatizar que una descripción estadística de un sistema cuántico también se aplica a un estado puro. Un postulado fundamental es que el valor de expectativa de un operador

\[\langle \hat {A} \rangle = \langle \psi | \hat {A} | \psi \rangle\]

es el valor medio\(A\) obtenido a lo largo de muchas observaciones en sistemas preparados idénticamente. La media y varianza de este valor de expectativa representan la incertidumbre cuántica fundamental en una medición.

Para llevar esto un paso más allá y caracterizar la relación estadística entre dos variables, se puede definir una distribución de probabilidad conjunta\(P(A,B)\),, que caracteriza la probabilidad de observar\(A\) entre\(A\) y\(A+dA\) y\( B\) entre\(B\) y \(B+dB\). La relación estadística entre las variables también puede emerger de momentos de\(P(A,B)\). La medida más importante es una función de correlación

\[C _ {A B} = \langle A B \rangle - \langle A \rangle \langle B \rangle \label{8.8}\]

Se puede ver que esta es la covarianza, la varianza para una distribución bivariada. Esta es una medida de la correlación entre las variables\(A\) y\(B\). Es decir, para un valor específico de\(A\), para qué sirven las estadísticas asociadas\(B\). Para interpretar esto ayuda a definir un coeficiente de correlación

\[r = \frac {C _ {A B}} {\sigma _ {A} \sigma _ {B}} \label{8.9}\]

\(r\)puede tomar valores de +1 a -1. Si\(r = 1\) entonces existe una correlación perfecta entre las dos distribuciones. Si las variables\(A\) y\(B\) dependen de la misma manera de una variable interna común, entonces se correlacionan. Si no existe una relación estadística entre las dos distribuciones, entonces no están correlacionadas,\(r = 0\), y\(\langle A B \rangle = \langle A \rangle \langle B \rangle\). También es posible que las distribuciones dependan de manera igual y opuesta de una variable interna, en cuyo caso las llamamos anticorrelacionadas con\(r = -1\).