13.1: El modelo de oscilador armónico desplazado

Aquí discutiremos el oscilador armónico desplazado (DHO), un modelo ampliamente utilizado que describe el acoplamiento de movimientos nucleares a estados electrónicos. Aunque tiene muchas aplicaciones, veremos el ejemplo específico de experimentos de absorción electrónica, y así obtendremos una idea de la estructura vibrónica en los espectros de absorción. Espectroscópicamente, también se puede utilizar para describir la dinámica de las ondas; el acoplamiento de estados electrónicos y vibracionales a vibraciones intramoleculares o solventes; o el acoplamiento de estados electrónicos en sólidos o semiconductores a fonones. Como veremos, se pueden usar más extensiones de este modelo para describir procesos de tasa química fundamental, interacciones de una molécula con un ambiente disipativo o fluctuante, y la Teoría de Marcus para la transferencia de electrones no adiabáticos.

El DHO y la Absorción Electrónica

Los estados excitados moleculares tienen geometrías que son diferentes de la configuración del estado fundamental como resultado de la configuración de los electrones variables. Esta dependencia paramétrica de la energía electrónica en la configuración nuclear resulta en una variación de la brecha de energía electrónica entre estados a medida que uno estira las vibraciones de enlace de la molécula. Nos interesa describir cómo este efecto influye en el espectro de absorción electrónica, y así obtener una idea de cómo se determina experimentalmente el acoplamiento entre los grados de libertad electrónica y nuclear. Consideramos transiciones electrónicas entre superficies de energía potencial ligadas para un estado terrestre y excitado a medida que desplazamos una coordenada nuclear\(q\). El modelo simplificado consiste en dos potenciales de osciladores armónicos cuya división de energía 0-0 es\(E _ {e} - E _ {g}\) y de la que depende\(q\). Calcularemos el espectro de absorción en la imagen de interacción usando la función de correlación de tiempo para el operador dipolo.

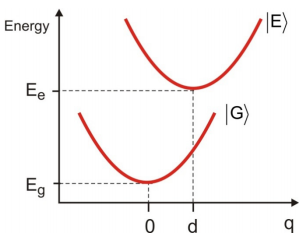
Comenzamos por escribir un hamiltoniano que contiene dos términos para las superficies de energía potencial del estado electrónicamente excitado\(| E \rangle\) y el estado fundamental\(| G \rangle\)

\[H _ {0} = H _ {G} + H _ {E} \label{12.1}\]

Estos términos describen la dependencia de la energía electrónica en el desplazamiento de una coordenada nuclear\(q\). Dado que el estado del sistema depende paramétricamente del nivel de excitación vibratoria, lo describimos usando estados de producto en la configuración electrónica y nuclear\(| \Psi \rangle = | \psi _ {\text {elec}} , \Phi _ {n u c} \rangle\), o en el presente caso

\[\begin{align} | G \rangle &= | g , n _ {g} \rangle \\[4pt] | E \rangle &= | e , n _ {e} \rangle \label{12.2} \end{align}\]

Implícita en este modelo hay una aproximación Born-Oppenheimer en la que los estados del producto son los autoestados de\(H_0\), i.e.

\[H _ {G} | G \rangle = \left( E _ {g} + E _ {n _ {g}} \right) | G \rangle\]

El hamiltoniano para cada superficie contiene una energía electrónica en ausencia de excitación vibratoria, y un hamiltoniano vibrónico que describe el cambio en la energía con el desplazamiento nuclear.

\[\begin{align} H _ {G} & = | g \rangle E _ {g} \langle g | + H _ {g} ( q ) \\[4pt] H _ {E} & = | e \rangle E _ {e} \langle e | + H _ {e} ( q ) \label{12.3} \end{align}\]

Para nuestros propósitos, el hamiltoniano vibrónico es armónico y tiene la misma curvatura en el suelo y estados excitados, sin embargo, el estado excitado es desplazado por d con relación al estado fundamental a lo largo de una coordenada\(q\).

\[\begin{align} H _ {g} &= \frac {p^{2}} {2 m} + \frac {1} {2} m \omega _ {0}^{2} q^{2} \label{12.4} \\[4pt] H _ {e} &= \frac {p^{2}} {2 m} + \frac {1} {2} m \omega _ {0}^{2} ( q - d )^{2} \label{12.5} \end{align}\]

El operador\(q\) actúa solo para cambiar el grado de excitación vibratoria en la\(| G \rangle\) superficie\(| E \rangle\) o.

Ahora deseamos evaluar la función de correlación dipolo

\[\begin{align} C _ {\mu \mu} (t) & = \langle \overline {\mu} (t) \overline {\mu} ( 0 ) \rangle \\[4pt] & = \sum _ {\ell = E , G} p _ {\ell} \left\langle \ell \left| e^{i H _ {0} t / h} \overline {\mu} e^{- i H _ {0} t / h} \overline {\mu} \right| \ell \right\rangle \label{12.6} \end{align} \]

Aquí\(p_{\ell}\) está la probabilidad conjunta de ocupar un determinado estado electrónico y vibracional,\(p _ {\ell} = p _ {\ell , e l e c} p _ {\ell , v i b}\). El propagador del tiempo es

\[e^{- i H _ {d} t / h} = | G \rangle e^{- i H _ {c} t h} \langle G | + | E \rangle e^{- i H _ {E} t / h} \langle E | \label{12.7}\]

Comenzamos por hacer la Aproximación del Condón, que establece que no hay dependencia nuclear para el operador dipolo. Es sólo un operador en los estados electrónicos.

\[\overline {\mu} = | g \rangle \mu _ {g e} \langle e | + | e \rangle \mu _ {e g} \langle g | \label{12.8}\]

Esta aproximación implica que las transiciones entre superficies electrónicas ocurren sin un cambio en las coordenadas nucleares, que en un diagrama de energía potencial es una transición vertical.

Bajo condiciones típicas, el sistema solo estará sobre el terreno en estado electrónico en equilibrio, y sustituyendo las Ecuaciones\ ref {12.7} y\ ref {12.8} en la Ecuación\ ref {12.6}, encontramos:

\[C _ {\mu \mu} (t) = \left| \mu _ {e g} \right|^{2} e^{- i \left( E _ {e} - E _ {g} \right) t h} \left\langle e^{i H _ {g} t h} e^{- i H _ {\ell} t / h} \right\rangle \label{12.9}\]

Aquí las oscilaciones en la brecha de energía electrónica se separan de la dinámica nuclear en el factor final, la función de desfase:

\[\begin{align} F (t) & = \left\langle e^{i H _ {g} t / \hbar} e^{- i H _ {c} t / h} \right\rangle \\[4pt] & = \left\langle U _ {g}^{\dagger} U _ {e} \right\rangle \label{12.10} \end{align}\]

El promedio\(\langle \ldots \rangle\) en Ecuaciones\ ref {12.9} y\ ref {12.10} es solo por encima de los estados vibracionales\(| n _ {g} \rangle\). Tenga en cuenta que físicamente la función de desfase describe la superposición dependiente del tiempo de la función de onda nuclear en el estado fundamental con la evolución temporal de la misma paquete de ondas proyectada inicialmente sobre el estado excitado

\[F (t) = \left\langle \varphi _ {g} (t) | \varphi _ {e} (t) \right\rangle \label{12.11}\]

Esta es una expresión perfectamente general que no depende de la forma particular del potencial. Si tienes conocimiento de los estados propios nucleares y electrónicos o de la dinámica nuclear en tu terreno y superficies de estado excitado, esta expresión es tu ruta hacia el espectro de absorción.

Para más información sobre esto ver:

• Schatz, G. C.; Ratner, M. A., Mecánica Cuántica en Química. Publicaciones de Dover: Mineola, NY, 2002; Ch. 9.
• Reimers, J. R.; Wilson, K. R.; Heller, E. J., Técnica compleja de paquetes de ondas dependientes del tiempo para sistemas de equilibrio térmico: Espectros electrónicos. J. Chem. Phys. 1983, 79, 4749-4757. 12-4

\(F(t)\)Para evaluar este problema, ayuda a darnos cuenta de que podemos escribir a los hamiltonianos nucleares como

\[\begin{align} H _ {g} &= \hbar \omega _ {0} \left( a^{\dagger} a + \ce{1/2} \right) \label{12.12} \\[4pt] H _ {e} &= \hat {D} H _ {g} \hat {D}^{\dagger} \label{12.13} \end{align} \]

Aquí\(\hat {D}\) está el operador de desplazamiento espacial

\[\hat {D} = \exp ( - i \hat {p} d / \hbar ) \label{12.14}\]

que desplaza a un operador en el espacio como:

\[\hat {D} \hat {q} \hat {D}^{\dagger} = \hat {q} - d \label{12.15}\]

Note\(\hat{p}\) es solo un operador en el grado de libertad vibracional. Ahora podemos expresar el estado excitado hamiltoniano en términos de un estado fundamental desplazado hamiltoniano en la Ecuación\ ref {12.13}, y también relacionar los propagadores del tiempo en el suelo y los estados excitados

\[e^{- i H _ {c} t / h} = \hat {D} e^{- i H _ {g} t / h} \hat {D}^{\dagger} \label{12.16}\]

Sustituir la ecuación\ ref {12.16} en la ecuación\ ref {12.10} nos permite escribir

\[\begin{align} F (t) & = \left\langle U _ {g}^{\dagger} e^{- i d p / h} U _ {g} e^{i d p / h} \right\rangle \\ & = \left\langle \hat {D} (t) \hat {D}^{\dagger} ( 0 ) \right\rangle \label{12.17} \end{align}\]

La ecuación\ ref {12.17} dice que el efecto del movimiento nuclear en la función de correlación dipolo se puede expresar como una función de correlación de tiempo para el desplazamiento de la vibración.

Para evaluar la Ecuación\ ref {12.17} la escribimos como

\[F (t) = \left\langle e^{- i d \hat {p} (t) / \hbar} e^{i d \hat {p} ( 0 ) / \hbar} \right\rangle \label{12.18}\]

desde

\[\hat {p} (t) = U _ {g}^{\dagger} \hat {p} ( 0 ) U _ {g} \label{12.19}\]

La evolución temporal de\(\hat{p}\) se obtiene expresándola en forma de operador de elevación y descenso,

\[\hat {p} = i \sqrt {\frac {m \hbar \omega _ {0}} {2}} \left( a^{\dagger} - a \right) \label{12.20}\]

y evaluando la Ecuación\ ref {12.19} usando la Ecuación\ ref {12.12}. Recordando\(a^{\dagger} a = n\), encontramos

\[\left. \begin{array} {l} {U _ {g}^{\dagger} a U _ {g} = e^{i n \omega _ {0} t} a e^{- i n \omega _ {0} t} = a e^{i ( n - 1 ) \omega _ {0} t} e^{- i n \omega _ {0} t} = a e^{- i \omega _ {0} t}} \\ {U _ {g}^{\dagger} a^{\dagger} U _ {g} = a^{\dagger} e^{+ i \omega _ {0} t}} \end{array} \right. \label{12.21}\]

lo que da

\[\hat {p} (t) = i \sqrt {\frac {m \hbar \omega _ {0}} {2}} \left( a^{\dagger} e^{i \omega _ {0} t} - a e^{- i \omega _ {0} t} \right) \label{12.22}\]

Así que para la función de desfase ahora tenemos

\[F (t) = \left\langle \exp \left[ d \left( a^{\dagger} e^{i \omega _ {0} t} - a e^{- i \omega _ {0} t} \right) \right] \exp \left[ - d \left( a^{\dagger} - a \right) \right] \right\rangle \label{12.23}\]

donde hemos definido una variable de desplazamiento adimensional

\[\underset{\sim}{d} = d \sqrt {\frac {m \omega _ {0}} {2 \hbar}} \label{12.24}\]

Desde\(a^{\dagger}\) y\(a\) no conmutar (\(\left[ a^{\dagger} , a \right] = - 1\)), dividimos los operadores exponenciales usando la identidad

\[e^{\hat {A} + \hat {B}} = e^{\hat {A}} e^{\hat {B}} e^{- \frac {1} {2} [ \hat {A} , \hat {B} ]} \label{12.25}\]

o específicamente para\(a^{\dagger}\) y\(a\),

\[e^{\lambda a^{\dagger} + \mu a} = e^{\lambda a^{\dagger}} e^{\mu a} e^{\frac {1} {2} \lambda \mu} \label{12.26}\]

Esto lleva a

\[ F (t) = \left \langle \exp \left[ \underset{\sim}{d} \,a^{\dagger}\, e^{i \omega _ {0} t} \right] \exp \left[ - \underset{\sim}{d}\, a\, e^{- i \omega _ {0} t} \right] \exp \left[ - \frac {1} {2} \underset{\sim}{d}^{2} \right] \exp \left[ - \underset{\sim}{d}\, a^{\dagger} \right] \exp [ \underset{\sim}{d}\, a ] \exp \left[ - \frac {1} {2} \underset{\sim}{d}^{2} \right] \right \rangle \label{12.27}\]

Ahora para simplificar aún más nuestro trabajo, consideremos específicamente el caso de baja temperatura en el que solo estamos en el estado vibratorio del suelo en equilibrio\(| n _ {s} \rangle = | 0 \rangle\). Desde\(a | 0 \rangle = 0\) y\(\langle 0 | a^{t} = 0\)

\[ \begin{align} e^{-\lambda a} | 0 \rangle &= | 0 \rangle \\[4pt] \langle 0 | e^{\lambda a^{\dagger}} &= \langle 0 | \label{12.28} \end{align} \]

y

\[F (t) = e^{- \underset{\sim}{d}^{2}} \left\langle 0 \left| \exp \left[ - \underset{\sim}{d} a e^{- i \omega _ {b} t} \right] \exp \left[ - \underset{\sim}{d} a^{\dagger} \right] \right| 0 \right \rangle \label{12.29}\]

En principio se trata de expresiones en las que podemos evaluar expandiendo los operadores exponenciales. Sin embargo, la evaluación se vuelve mucho más fácil si podemos intercambiar el orden de los operadores. Recordando que estos operadores no se desplazan, y usando

\[e^{\hat {A}} e^{\hat {B}} = e^{\hat {B}} e^{\hat {A}} e^{- [ \hat {B} , \hat {A} ]} \label{12.30}\]

nosotros podemos escribir

\[\begin{align} F (t) & {= e^{- \underset{\sim}{d}^{2}} \langle 0 \left| \exp \left[ - \underset{\sim}{d} a^{\dagger} \right] \exp \left[ - \underset{\sim}{d} \,a \, e^{- i \omega _ {0} t} \right] \exp \left[ \underset{\sim}{d}^{2} e^{- i \omega _ {0} t} \right] \| _ {0} \right\rangle} \\ & = \exp \left[ \underset{\sim}{d}^{2} \left( e^{- i \omega _ {0} t} - 1 \right) \right] \label{12.31} \end{align}\]

Entonces, finalmente, tenemos la función de correlación dipolo:

\[C _ {\mu \mu} (t) = \left| \mu _ {e g} \right|^{2} \exp \left[ - i \omega _ {e g} t + D \left( e^{- i \omega _ {v} t} - 1 \right) \right] \label{12.32}\]

\(D\)se conoce como el parámetro Huang-Rhys (que debe distinguirse del operador de desplazamiento\(\hat{D}\)). Es un factor adimensional relacionado con el desplazamiento cuadrático medio

\[D = d^{2} = \underset{\sim}{d}^{2} \frac {m \omega _ {0}} {2 \hbar} \label{12.33}\]

y por lo tanto representa la fuerza del acoplamiento de los estados electrónicos al grado de libertad nuclear. Tenga en cuenta que nuestra función de correlación tiene la forma

\[C _ {\mu \mu} (t) = \sum _ {n} p _ {n} \left| \mu _ {m n} \right|^{2} e^{- i \omega _ {m n} t - g (t)} \label{12.34}\]

Aquí\(g(t)\) está nuestra función de lineshape

\[g (t) = - D \left( e^{- i \omega _ {0} t} - 1 \right) \label{12.35}\]

Para ilustrar la forma de estas funciones, a continuación se trazan las partes reales e imaginarias de\(C _ {\mu \mu} (t)\),\(F(t)\),\(g(t)\) para\(D = 1\), y\(\omega_{eg} = 10\omega_0\). \(g(t)\)oscila con la frecuencia del modo vibratorio único. \(F(t)\)cuantifica la superposición de paquetes de ondas vibracionales en el suelo y el estado excitado, que alcanza su punto máximo una vez cada período vibracional. \(C _ {\mu \mu} (t)\)tiene la misma información que\(F(t)\), pero también se modula en la brecha de energía electrónica\(\omega_{eg}\).

Figura\(\PageIndex{3}\)

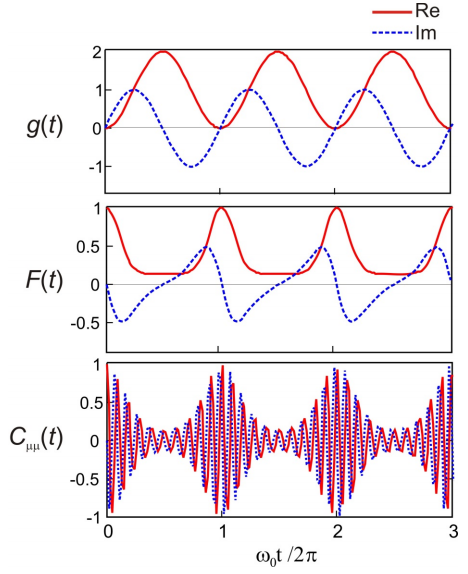
Absorción Lineshape y Franck-Condon Transiciones

El lineshape de absorción se obtiene mediante la ecuación transformadora de Fourier\ ref {12.32}

\[\begin{align} \sigma _ {a b s} ( \omega ) & = \int _ {- \infty}^{+ \infty} d t \,e^{i \omega t} C _ {\mu \mu} (t) \\[4pt] & = \left| \mu _ {e g} \right|^{2} e^{- D} \int _ {- \infty}^{+ \infty} d t\, e^{i \omega t} e^{- i \omega _ {e s} t} \exp \left[ D e^{- i \omega _ {0} t} \right] \label{12.36} \end{align}\]

Si ahora ampliamos el término final como

\[\exp \left[ D \mathrm {e}^{- i \omega _ {0} t} \right] = \sum _ {n = 0}^{\infty} \frac {1} {n !} D^{n} \left( e^{- i \omega _ {0} t} \right)^{n} \label{12.37}\]

el lineshape es

\[\sigma _ {a b s} ( \omega ) = \left| \mu _ {e g} \right|^{2} \sum _ {n = 0}^{\infty} e^{- D} \frac {D^{n}} {n !} \delta \left( \omega - \omega _ {e g} - n \omega _ {0} \right) \label{12.38}\]

El espectro es una progresión de los picos de absorción que se elevan desde\(\omega_{eg}\), separados por\(\omega_0\) una distribución de Poisson de intensidades. Se trata de una progresión vibracional que acompaña a la transición electrónica. La amplitud de cada uno de estos picos viene dada por los coeficientes Franck—Condon para la superposición de estados vibracionales en los estados suelo y excitado

\[\left| \left\langle n _ {g} = 0 | n _ {e} = n \right\rangle \right|^{2} = | \langle 0 | \hat {D} | n \rangle |^{2} = e^{- D} \frac {D^{n}} {n !}\]

Las intensidades de estos picos dependen de\(D\), lo que es una medida de la fuerza de acoplamiento entre los grados de libertad nuclear y electrónica. A continuación se ilustra un ejemplo de la forma de línea de absorción normalizada correspondiente a la función de correlación para\(D = 1\) en la Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\)

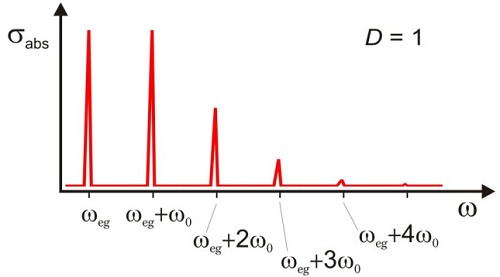
Ahora investiguemos de qué depende el lineshape de absorción\(D\).

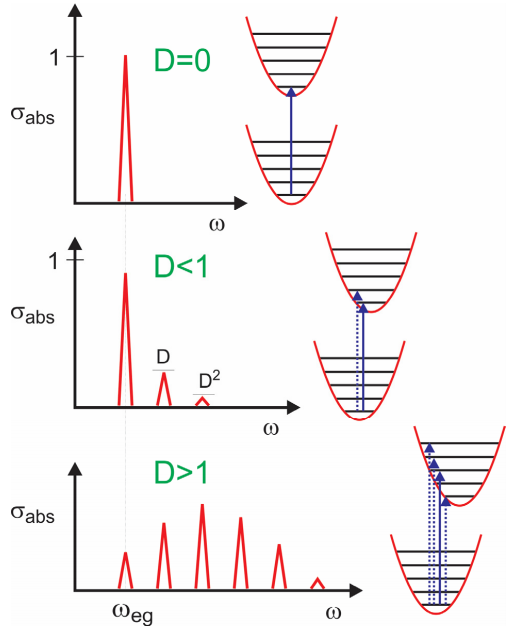
Porque\(D = 0\), no hay dependencia de la brecha de energía electrónica de\(\omega_{eg}\) la coordenada nuclear, y sólo se observa una resonancia. Porque\(D < 1\), la dependencia de la brecha de energía en\(q\) es débil y el máximo de absorción está en\(\omega_{eg}\), con la amplitud de la progresión vibrónica cayendo como\(D^n\). Para\(D >1\), el régimen de acoplamiento fuerte, la transición con la intensidad máxima se encuentra para pico en\(n \approx D\). Así\(D\) corresponde aproximadamente al número medio de cuantos vibracionales excitados desde\(q = 0\) en el estado fundamental. Este es el principio Franck-Condon, que las intensidades de transición son dictadas por el solapamiento vertical entre las funciones de onda nuclear en las dos superficies electrónicas.

Para investigar la envolvente de estas transiciones, podemos realizar una expansión de corto tiempo de la función de correlación aplicable para\(t < 1/\omega_{0}\) y para\(D \gg 1\). Si aproximamos el término oscilatorio en la función lineshape como

\[\exp \left( - i \omega _ {0} t \right) \approx 1 - i \omega _ {0} t - \frac {1} {2} \omega _ {0}^{2} t^{2} \label{12.40}\]

entonces el sobre de la forma de línea es

\[\begin{align} \sigma _ {e n v} ( \omega ) & = \left| \mu _ {e g} \right|^{2} \int _ {- \infty}^{+ \infty} d t e^{i \omega t} e^{- i \omega _ {e g} t} e^{D \left( \exp \left( - i \omega _ {0} t \right) - 1 \right)} \\ & \approx \left| \mu _ {e g} \right|^{2} \int _ {- \infty}^{+ \infty} d t e^{i \left( \omega - \omega _ {e g} t \right)} e^{D \left[ - i \omega _ {0} t - \frac {1} {2} \omega _ {0}^{2} t^{2} \right]} \\ & = \left| \mu _ {e g} \right|^{2} \int _ {- \infty}^{+ \infty} d t e^{i \left( \omega - \omega _ {e g} - D \omega _ {0} \right) t} e^{- \frac {1} {2} D \omega _ {0}^{2} t^{2}} \label{12.41} \end{align}\]

Esto se puede resolver completando la plaza, dando

\[\sigma _ {e n v} ( \omega ) = \left| \mu _ {e g} \right|^{2} \sqrt {\frac {2 \pi} {D \omega _ {0}^{2}}} \exp \left[ - \frac {\left( \omega - \omega _ {e g} - D \omega _ {0} \right)^{2}} {2 D \omega _ {0}^{2}} \right] \label{12.42}\]

La envolvente tiene un perfil gaussiano centrado en la transición vertical Franck—Condon

\[\omega = \omega _ {e g} + D \omega _ {0} \label{12.43}\]

Así podemos equiparar\(D\) con el número medio de cuantos vibracionales excitados\(| E \rangle\) en la absorción desde el estado fundamental. También, podemos definir la energía vibratoria de energía vibratoria\(| E \rangle\) en la excitación en\(q=0\)

\[ \begin{align} \lambda &= D \hbar \omega _ {0} \\[4pt] &= \frac {1} {2} m \omega _ {0}^{2} d^{2} \label{12.44} \end{align}\]

\(\lambda\)se conoce como la energía de reorganización. Este es el valor de\(H_e\) at\(q=0\), que refleja el exceso de excitación vibratoria en el estado excitado que se produce en una transición vertical desde el estado fundamental. Por lo tanto, es la energía la que debe ser disipada por la relajación vibratoria en la superficie del estado excitado a medida que el sistema se reequilibre después de la absorción.

Figura FC1.png "src=”/@api /deki/files/142180/Figure_FC1.png "/>

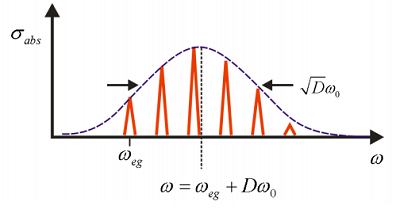
Ilustración de cómo la fuerza del acoplamiento\(D\) influye en la forma de línea de absorción\(\sigma\) (Ecuación\ ref {12.38}) y la función de correlación dipolo\(C _ {\mu \mu}\) (Ecuación\ ref {12.32}).

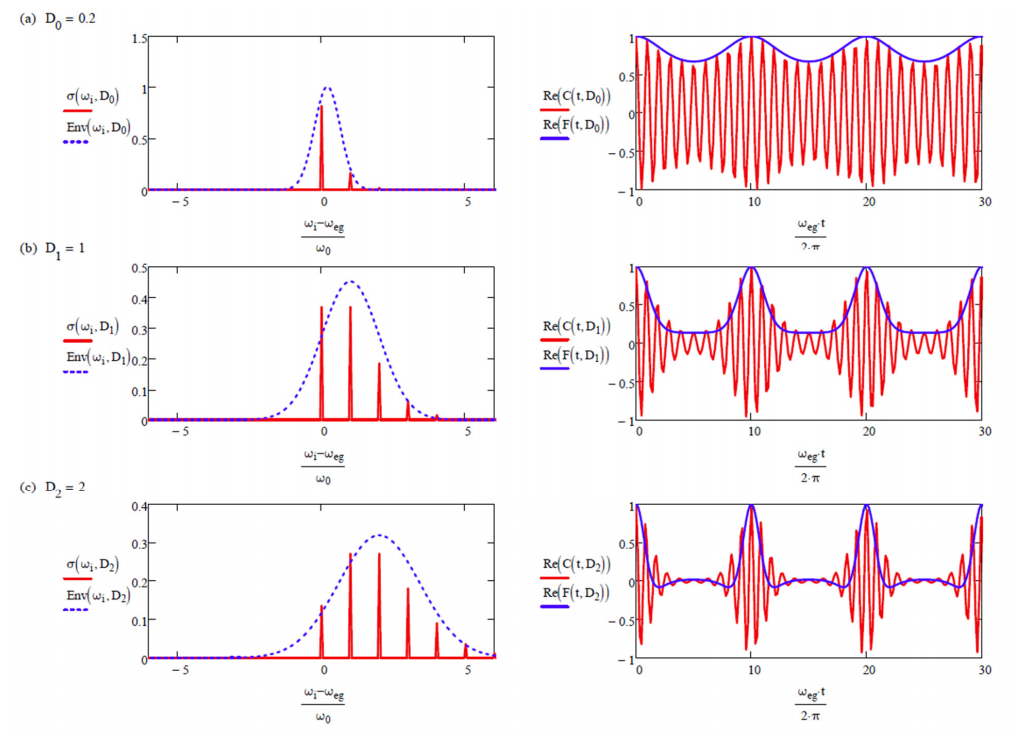
También se muestra la aproximación gaussiana al perfil de absorción (Ecuación\ ref {12.42}), y la función de desfase (Ecuación\ ref {12.31}).

Fluorescencia

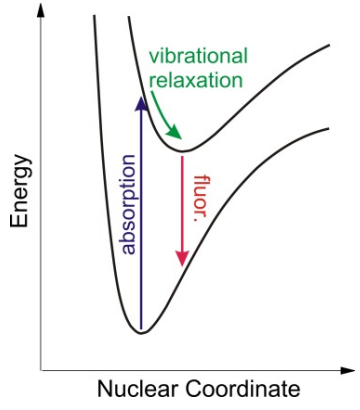
El modelo DHO también conduce a predicciones sobre la forma del espectro de emisión a partir del estado electrónicamente excitado. La excitación vibratoria en la superficie de energía potencial del estado excitado inducida por absorción electrónica se disipa rápidamente a través de la relajación vibratoria, típicamente en escalas de tiempo de picosegundos. La relajación vibratoria deja el sistema en el estado vibratorio del suelo de la superficie excitada electrónicamente, con un desplazamiento promedio que es mayor que el del estado fundamental. En ausencia de otros procesos no radiativos procesos de relajación, la forma más eficiente de relajarse de nuevo al estado fundamental es mediante emisión de luz, es decir, fluorescencia. En la aproximación del Condón esto ocurre a través de transiciones verticales desde el estado excitado mínimo a un estado vibracionalmente excitado en la superficie electrónica del suelo. La diferencia entre las frecuencias de absorción y emisión refleja la energía de la excitación inicial que se ha disipado no radiativamente en movimiento vibratorio tanto en los estados electrónicos excitados como terrestres, y se conoce como el desplazamiento de Stokes.

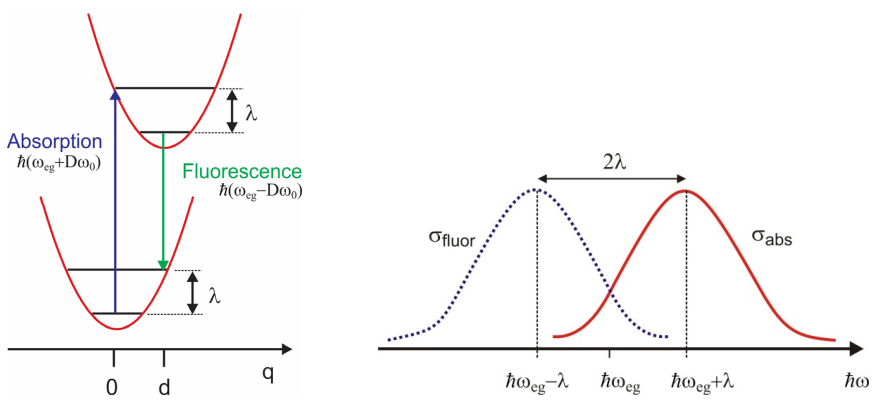
A partir del modelo DHO, la forma de línea de emisión se puede obtener de la función de correlación dipolo asumiendo que el estado inicial se equilibre en\(| e , 0 \rangle\), centrado en un desplazamiento\(q= d\), siguiendo la rápida disipación de energía\(\lambda\) en el estado excitado. Con base en la brecha de energía en\(q=d\), vemos que una emisión vertical desde este punto sale\(\lambda\) como la energía vibracional que necesita ser disipada en el estado básico para reequilibrar, y por lo tanto esperamos que el cambio de Stokes sea\(2\lambda\)

Comenzando con nuestra derivación original de la función de correlación dipolo y enfocándonos en la emisión, encontramos que la fluorescencia es descrita por

\[\begin{align} C _ {\Omega} & = \langle e , 0 | \mu (t) \mu ( 0 ) | e , 0 \rangle = C _ {\mu \mu}^{*} (t) \\ & = \left| \mu _ {e g} \right|^{2} e^{- i \omega _ {\mathrm {g}} t} F^{*} (t) \label{12.45} \\[4pt] F^{*} (t) & = \left\langle U _ {e}^{\dagger} U _ {g} \right\rangle \\[4pt] & = \exp \left[ D \left( e^{i \omega _ {0} t} - 1 \right) \right] \label{12.46} \end{align}\]

Tomamos nota de que\(C _ {\mu \mu}^{*} (t) = C _ {\mu \mu} ( - t )\) y\(F^{*} (t) = F ( - t )\).

Entonces podemos obtener el espectro de fluorescencia

\[\begin{align} \sigma _ {f} ( \omega ) & = \int _ {- \infty}^{+ \infty} d t \,e^{i \omega t} C _ {\mu \mu}^{*} (t) \\[4pt] & = \left| \mu _ {e g} \right|^{2} \sum _ {n = 0}^{\infty} e^{- D} \frac {D^{n}} {n !} \delta \left( \omega - \omega _ {e g} + n \omega _ {0} \right) \end{align} \label{12.47}\]

Se trata de un espectro con las mismas características que el espectro de absorción, aunque con simetría especular alrededor\(\omega_{eg}\).

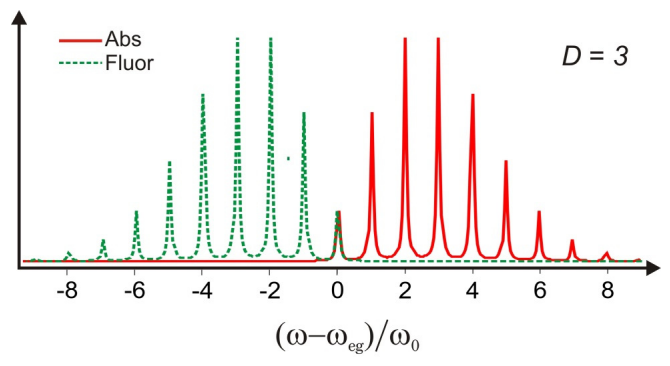
Una expansión de corto tiempo confirma que la división entre el pico de las envolturas de forma de línea de absorción y emisión es\(2 D \hbar \omega_0\), o\(2\lambda\). Además, se puede establecer que

\[\left.\begin{aligned} \sigma _ {a b s} ( \omega ) & = \int _ {- \infty}^{+ \infty} dt\, e^{i \left( \omega - \omega _ {e g} \right) t + g (t)} \\ \sigma _ {f l} ( \omega ) & = \int _ {- \infty}^{+ \infty} dt\, e^{i \left( \omega - \omega _ {e g} \right) t + g^{*} (t)} \\ g (t) & = D \left( e^{- i \omega _ {0} t} - 1 \right) \end{aligned} \right. \label{12.48}\]

Tenga en cuenta que nuestra descripción de la forma de línea de fluorescencia surgió de nuestro tratamiento semiclásico de la interacción luz-materia, y en la práctica la fluorescencia implica la emisión espontánea de luz a un campo de luz mecánica cuántica. Sin embargo, si bien el campo de luz debe manejarse de manera diferente, la forma de la función de correlación dipolo y la forma de línea resultante permanece sin cambios. Adicionalmente, asumimos que hubo una separación de escala de tiempo entre la relajación vibracional en el estado excitado y la escala de tiempo de emisión, de manera que el sistema puede considerarse balanceado en\(| e , 0 \rangle\). Cuando esta suposición no es válida entonces se debe dar cuenta de la posibilidad mucho más compleja de emisión durante el transcurso del proceso de relajación.

Lecturas

1. Mukamel, S., Principios de Espectroscopia Óptica No Lineal. Oxford University Press: Nueva York, 1995; p. 189, p. 217.
2. Nitzan, A., Dinámica Química en Fases Condensadas. Oxford University Press: Nueva York, 2006; Sección 12.5.
3. Reimers, J. R.; Wilson, K. R.; Heller, E. J., Técnica compleja de paquetes de ondas dependientes del tiempo para sistemas de equilibrio térmico: Espectros electrónicos. J. Chem. Phys. 1983, 79, 4749-4757.
4. Schatz, G. C.; Ratner, M. A., Mecánica Cuántica en Química. Publicaciones de Dover: Mineola, NY, 2002; Ch. 9.