13.2: Acoplamiento a un Baño Armónico

Cabe destacar una similitud entre el hamiltoniano para este problema del oscilador armónico desplazado, y una forma general para la interacción de un “sistema” electrónico que se observa en un experimento con un oscilador armónico “baño” cuyos grados de libertad son invisibles a lo observable, pero que influyen el comportamiento del sistema. Este razonamiento, de hecho, se desarrollará más cuidadosamente más adelante para la descripción de las fluctuaciones. Mientras que los hamiltonianos que hemos escrito hasta ahora describen el acoplamiento a un solo grado de libertad de baño, el modelo DHO se generaliza fácilmente a muchas vibraciones o un continuo de movimientos nucleares. El acoplamiento a un continuo, o un baño armónico, es el punto de partida para desarrollar cómo un sistema electrónico interactúa con un continuo de movimientos intermoleculares y fonones típicos de los sistemas de fase condensada.

Entonces, ¿qué pasa si la transición electrónica se acopla a muchas coordenadas vibracionales, cada una con su propio desplazamiento? La extensión es sencilla si todavía solo consideramos dos estados electrónicos (\(e\)y\(g\)) a los que acoplamos un conjunto de modos independientes, es decir, un baño de modos normales armónicos. Entonces podemos escribir el hamiltoniano para\(N\) vibraciones como una suma sobre todos los modos armónicos independientes

\[H _ {e} = \sum _ {\alpha = 1}^{N} H _ {e}^{( \alpha )} = \sum _ {\alpha = 1}^{N} \left( \frac {p _ {\alpha}^{2}} {2 m _ {\alpha}} + \frac {1} {2} m _ {\alpha} \omega _ {a}^{2} \left( q _ {\alpha} - d _ {\alpha} \right)^{2} \right) \label{12.49}\]

cada uno con su distinta frecuencia y desplazamiento. Podemos precisar el estado del sistema en términos de estados de producto en la ocupación electrónica y nuclear, es decir,

\[\left.\begin{aligned} | G \rangle & = | g ; n _ {1} , n _ {2} , \ldots , n _ {N} \rangle \\ & = | g \rangle \prod _ {\alpha = 1}^{N} | n _ {\alpha} \rangle \end{aligned} \right. \label{12.50}\]

Adicionalmente, reconocemos que el propagador de tiempo en la superficie electrónica de energía potencial excitada es

\[U _ {e} = \exp \left[ - \frac {i} {\hbar} H _ {e} t \right] = \prod _ {\alpha = 1}^{N} U _ {e}^{( \alpha )} \label{12.51}\]

donde

\[U _ {e}^{( \alpha )} = \exp \left[ - \frac {i} {\hbar} H _ {e}^{( \alpha )} t \right] \label{12.52}\]

Definiendo\(D _ {\alpha} = d _ {\alpha}^{2} \left( m \omega _ {\alpha} / 2 \hbar \right)\)

\[\left.\begin{aligned} F^{( \alpha )} & = \left\langle \left[ U _ {g}^{( \alpha )} \right]^{\dagger} U _ {e}^{( \alpha )} \right\rangle \\ & = \exp \left[ D _ {\alpha} \left( e^{- i \omega _ {a} t} - 1 \right) \right] \end{aligned} \right. \label{12.53}\]

la función de correlación dipolo es entonces solo un producto de múltiples funciones de desfase que caracterizan la evolución temporal de las diferentes vibraciones.

\[C _ {\mu \mu} (t) = \left| \mu _ {e g} \right|^{2} e^{- i \omega _ {e g} t} \cdot \prod _ {\alpha = 1}^{N} F^{( \alpha )} (t) \label{12.54}\]

o

\[C _ {\mu \mu} (t) = \left| \mu _ {e g} \right|^{2} e^{- i \omega _ {e g} t + g (t)} \label{12.55}\]

con

\[g (t) = \sum _ {\alpha} D _ {\alpha} \left( e^{- i \omega _ {a} t} - 1 \right) \label{12.56}\]

En el dominio del tiempo se trata de un patrón de latido complejo, que en el dominio de la frecuencia aparece como un espectro con varias progresiones vibrónicas superpuestas que siguen las reglas desarrolladas anteriormente. Además, la energía de reorganización ahora refleja al exceso total de energía potencial nuclear requerida para hacer la transición electrónica:

\[\lambda = \sum _ {\alpha} D _ {\alpha} \hbar \omega _ {\alpha} \label{12.57}\]

Llevando esto un paso más allá, surge naturalmente la generalización a un continuo de estados nucleares. Dado que tenemos una distribución continua de frecuencias de modos normales caracterizada por una densidad de estados\(W(\omega)\), y un acoplamiento dependiente de la frecuencia continuamente variable\(D ( \omega )\), podemos cambiar la suma en la Ecuación\ ref {12.56} a una integral sobre la densidad de estados:

\[g (t) = \int d \omega \,W ( \omega ) D ( \omega ) \left( e^{- i \omega t} - 1 \right) \label{12.58}\]

Aquí el producto\(W ( \omega )D ( \omega )\) es una densidad de estados ponderada por acoplamiento, y comúnmente se conoce como densidad espectral.

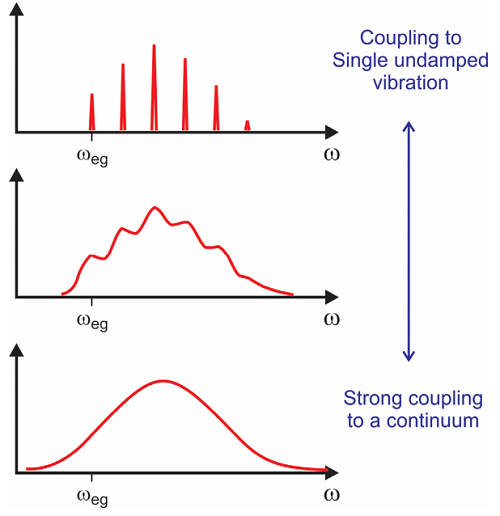
Lo que hace este tratamiento es proporcionar una forma de introducir un baño de estados con los que las parejas de transición interrogadas espectroscópicamente. El acoplamiento a un baño o continuo proporciona una manera de introducir efectos de relajación o amortiguación de la coherencia electrónica en el espectro de absorción. Se puede ver que si\(g(t)\) se asocia a una constante\(\Gamma\), obtenemos un lineshape lorentziano con ancho\(\Gamma\). Esto surge bajo ciertas circunstancias, por ejemplo si la distribución de estados y acoplamiento es grande y constante, y si la integral en la Ecuación\ ref {12.58} está sobre una distribución de bajas frecuencias, tal que\(e^{- i \omega t} \approx 1 - i \omega t\). De manera más general, la función lineshape es compleja, y la parte real describe la amortiguación y la parte imaginaria modula la frecuencia primaria y conduce a una estructura fina. Discutiremos estas circunstancias con más detalle más adelante.

Un conjunto a temperatura finita

Como se describió anteriormente, el modelo DHO monomodo anterior es para un estado puro, pero el enfoque se puede extender fácilmente para describir un conjunto canónico. En este caso, la función de correlación se promedia sobre una distribución térmica de estados iniciales. Si tomamos el estado inicial del sistema para estar en el estado básico electrónico y sus niveles vibracionales (\(n_g\)) para ser ocupados como una distribución de Boltzmann, que es característica de las muestras de temperatura ambiente, entonces la función de correlación dipolo puede escribirse como una desfase promediada térmicamente función:

\[C _ {\mu \mu} (t) = \left| \mu _ {e g} \right|^{2} e^{- i \omega _ {g} t} F (t) \label{12.59}\]

\[F (t) = \sum _ {n _ {g}} p \left( n _ {g} \right) \left\langle n _ {g} \left| U _ {g}^{\dagger} U _ {e} \right| n _ {g} \right\rangle \label{12.60}\]

\[p \left( n _ {g} \right) = \frac {e^{- \beta \ln a _ {b}}} {Z} \label{12.61}\]

Evaluar estas expresiones utilizando las estrategias desarrolladas anteriormente lleva a

\[C _ {\mu \mu} (t) = \left| \mu _ {e g} \right|^{2} e^{- i \omega _ {e g} t} \exp \left[ D \left[ ( \overline {n} + 1 ) \left( e^{- i \omega _ {0} t} - 1 \right) + \overline {n} \left( e^{+ i \omega _ {0} t} - 1 \right) \right] \right\rceil \label{12.62}\]

\(\overline {n}\)es el número de ocupación promediado térmicamente del modo vibratorio armónico.

\[\overline {n} = \left( e^{\beta \hbar \omega _ {0}} - 1 \right)^{- 1} \label{12.63}\]

Tenga en cuenta que en el límite de temperatura baja\(\overline {n} \rightarrow 0\),, y la Ecuación\ ref {12.62} es igual a nuestro resultado original Ecuación\ ref {12.32}. La función de desfase tiene dos términos subrayados en la Ecuación\ ref {12.62}, de los cuales el primero describe aquellos eventos de absorción electrónica en los que el número cuántico vibracional aumenta o se encuentra inalterado (\(n_e≥n_g\)), mientras que el segundo es para aquellos procesos donde el número cuántico vibracional disminuye o es sin cambios (\(n_e≤n_g\)). Estos últimos sólo se permiten a temperatura elevada donde se pueblan estados térmicamente excitados y se conocen como “bandas calientes”.

Ahora, calculemos el lineshape. Si separamos la función de desfase en un producto de dos términos exponenciales y expandimos cada uno de estos exponenciales, podemos transformar Fourier para dar

\[\sigma _ {a b s} ( \omega ) = \left| \mu _ {e g} \right|^{2} e^{- D ( 2 \overline {n} + 1 )} \sum _ {j = 0}^{\infty} \sum _ {k = 0}^{\infty} \left( \frac {D^{j + k}} {j ! k !} \right) ( \overline {n} + 1 )^{j} \overline {n}^{k} \delta \left( \omega - \omega _ {e g} - ( j - k ) \omega _ {0} \right) \label{12.64}\]

Aquí la suma sobre\(j\) describe\(n_e≥n_g\) las transiciones, mientras que la suma sobre\(k\) describe\(n_e≤n_g\). Para cualquier frecuencia de transición, (\(\omega \mathrm {eg}^{+} n \omega 0\)), la absorción neta es una suma sobre todas las combinaciones posibles de transiciones en la división de energía con\(n=(j-k)\). Nuevamente, si establecemos\(\overline {n} \rightarrow 0\), obtenemos nuestro resultado original Ecuación 13.1.47. Los aportes donde\(k<j\) lleva a las bandas calientes.

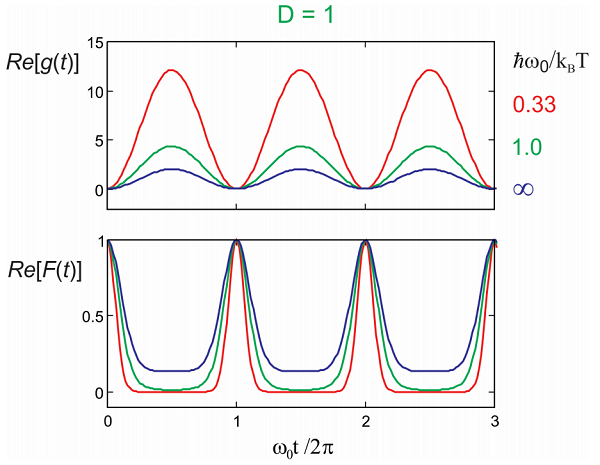
Ejemplos de dependencia de la temperatura a la forma de línea y funciones de desfase para\(D = 1\). La parte real cambia de amplitud, creciendo con la temperatura, mientras que la parte imaginaria no cambia.

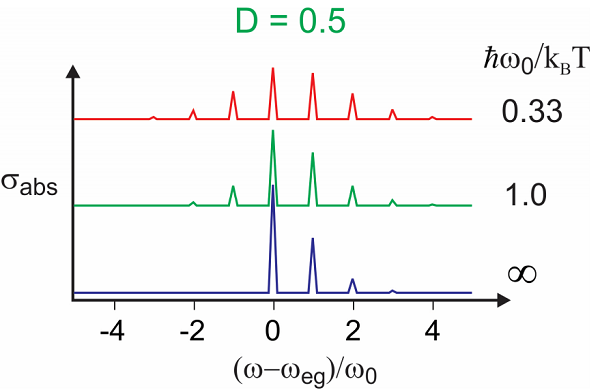
Podemos extender esta descripción para describir el acoplamiento a muchos modos nucleares independientes o el acoplamiento a un continuo. Escribimos el estado del sistema en términos del estado electrónico y los números cuánticos nucleares, es decir,\(| E \rangle = | e ; n _ {1} , n _ {2} , n _ {3} \dots \rangle\) y a partir de eso:

\[F (t) = \exp \left[ \sum _ {j} D _ {j} \left[ \left( \overline {n} _ {j} + 1 \right) \left( e^{- i \omega _ {j} t} - 1 \right) + \overline {n} _ {j} \left( e^{i \omega _ {j} t} - 1 \right) \right] \right] \label{12.65}\]

o cambiar a una integral sobre una distribución continua de frecuencias de modos normales caracterizados por una densidad de estados,\(W(\omega)\)

\[F (t) = \exp \left[ \int d \omega \, W ( \omega ) D ( \omega ) \left[ ( \overline {n} ( \omega ) + 1 ) \left( e^{- i \omega t} - 1 \right) + \overline {n} ( \omega ) \left( e^{i \omega t} - 1 \right) \right] \right] \label{12.66}\]

\(D ( \omega )\)es el acoplamiento dependiente de la frecuencia. Veamos la envolvente de la estructura nuclear en la transición haciendo una expansión a corto plazo sobre el exponencial complejo como en la Ecuación 13.1.49

\[F (t) = \exp \left[ \int d \omega \,D ( \omega ) W ( \omega ) \left( - i \omega t - ( 2 \overline {n} + 1 ) \frac {\omega^{2} t^{2}} {2} \right) \right] \label{12.67}\]

La forma de línea se calcula a partir de

\[\sigma _ {a b s} ( \omega ) = \int _ {- \infty}^{+ \infty} d t \,e^{i \left( \omega - \omega _ {e g} \right) t} \exp [ - i \langle \omega \rangle t ] \exp \left[ - \frac {1} {2} \left\langle \omega^{2} \right\rangle t^{2} \right] \label{12.68}\]

donde hemos definido la media de excitación vibratoria en la absorción

\[\begin{align} \langle \omega \rangle & = \int d \omega \, W ( \omega ) D ( \omega ) \omega \\[4pt] & = \lambda / \hbar \label{12.69} \end{align}\]

y

\[\left\langle \omega^{2} \right\rangle = \int d \omega\, W ( \omega ) D ( \omega ) \omega^{2} ( 2 \overline {n} ( \omega ) + 1 ) \label{12.70}\]

\(\left\langle \omega^{2} \right\rangle\)refleja la distribución promediada térmicamente de estados vibratorios accesibles. Completar el cuadrado de la Ecuación\ ref {12.68} da

\[\sigma _ {a b s} ( \omega ) = \left| \mu _ {e g} \right|^{2} \sqrt {\frac {2 \pi} {\left\langle \omega^{2} \right\rangle}} \exp \left[ \frac {- \left( \omega - \omega _ {e g} - \langle \omega \rangle \right)^{2}} {2 \left\langle \omega^{2} \right\rangle} \right] \label{12.71}\]

El lineshape es gaussiano, con un máximo de transición en la resonancia electrónica más energía de reorganización. Aunque el desplazamiento\(\langle \omega \rangle\) de frecuencia no depende de la temperatura, el ancho del gaussiano es dependiente de la temperatura como resultado del factor de ocupación térmica en la Ecuación\ ref {12.70}.