15.5: Teoría de Marcus para Transferencia de Electrones

El formalismo del oscilador armónico desplazado (DHO) y el Energy Gap Hamiltonian se han utilizado ampliamente para describir reacciones de transporte de carga, como la transferencia de electrones y protones. Aquí describimos las tasas de transferencia de electrones entre estados donador y aceptor débilmente acoplados cuando la energía potencial depende de una coordenada nuclear, es decir, transferencia de electrones no adiabática. Estos resultados reflejan los hallazgos de la teoría de Marcus sobre la transferencia de electrones.

Podemos representar el problema como calcular la transferencia o velocidad de reacción para la transferencia de un electrón de un donante a un aceptor

\[\ce{D + A \rightarrow D^{+} + A^{-}}\label{4.57}\]

Esta reacción está mediada por una coordenada nuclear\(q\). Esto no tiene por qué ser, y generalmente no lo es, una simple coordenada vibracional. Para la transferencia de electrones en solución, comúnmente consideramos que la transferencia de electrones progresa a lo largo de una coordenada de reordenamiento de solventes en la que el solvente reorganiza su configuración para que los dipolos o cargas ayuden a estabilizar la carga extra negativa en el sitio aceptor. Este tipo de coordenada colectiva se ilustra a continuación.

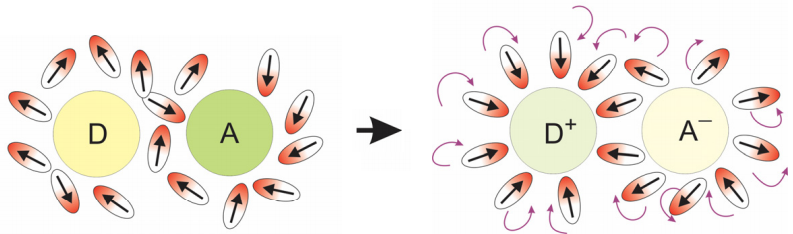
La respuesta externa del medio a lo largo de la coordenada de transferencia de electrones se conoce como transferencia de electrones de “capa externa”, mientras que la influencia de los modos vibratorios internos que promueven la ET se denomina “capa interna”. La influencia de reordenamientos colectivos de solventes o vibraciones intramoleculares se puede capturar con el uso de una transición electrónica acoplada a un baño armónico.

Normalmente asociamos las tasas de transferencia de electrones con la energía libre a lo largo de la coordenada de transferencia de electrones\(q\). Imágenes como las anteriores que ilustran estados del sistema con electrones localizados en el donador o aceptor de electrones saltando de donante a aceptor se representan conceptualmente a través de superficies de energía diabática. El acoplamiento electrónico\(J\) que da como resultado la transferencia mezcla estos estados diabáticos en la región de cruce. Desde esta superficie adiabática, la velocidad de transferencia para la reacción directa está relacionada con el flujo a través de la barrera. A partir de la teoría clásica del estado de transición podemos asociar la tasa con la barrera de energía libre utilizando

\[k _ {f} = A \exp \left( - \Delta G^{\dagger} / k _ {B} T \right)\]

Si el acoplamiento es débil, podemos describir las tasas de transferencia entre donante y aceptor en la base diabática con teoría de perturbación. Esto explica los efectos no adiabáticos y el túnel a través de la barrera.

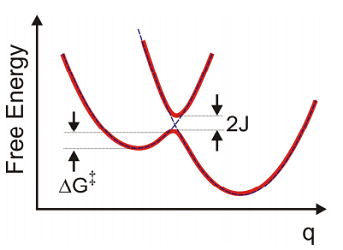
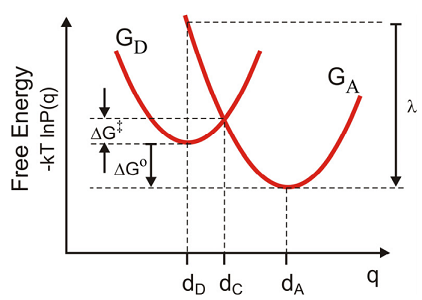
Para comenzar consideramos una derivación clásica simple para la barrera de energía libre y la tasa de transferencia de electrones de estados donadores a aceptores para el caso de estados diabáticos débilmente acoplados. Primero asumimos que la energía libre o potencial de fuerza media para el estado inicial y final,

\[\mathrm {G} ( \mathrm {q} ) = - \mathrm {k} _ {\mathrm {B}} \mathrm {T} \ln \mathrm {P} ( \mathrm {q} )\]

está bien representada por dos parábolas.

\[ \begin{align} G _ {D} ( q ) &= \frac {1} {2} m \omega _ {0}^{2} \left( q - d _ {D} \right)^{2} \label{14.58a} \\[4pt] G _ {A} ( q ) &= \frac {1} {2} m \omega _ {0}^{2} \left( q - d _ {A} \right)^{2} + \Delta G^{0} \label{14.58b} \end{align} \]

Para encontrar la altura de la barrera\(\Delta G^{\dagger}\), primero encontramos el punto de cruce\(dC\) donde

\[G_D(d_C) = G_A(d_C). \label{14.58c}\]

Sustituyendo ecuaciones\ ref {14.58a} y\ ref {14.58b} en Ecuación\ ref {14.58c}

\[ \frac {1} {2} m \omega _ {0}^{2} \left( d _ {c} - d _ {D} \right)^{2} = \Delta G^{\circ} + \frac {1} {2} m \omega _ {0}^{2} \left( d _ {C} - d _ {A} \right)^{2} \]

y resolviendo para\(d_C\) da

\[ \begin{align} d _ {C} &= \frac {\Delta G^{\circ}} {m \omega _ {0}^{2}} \left( \frac {1} {d _ {A} - d _ {D}} \right) + \frac {d _ {A} + d _ {D}} {2} \\[4pt] & = \frac {\Delta G^{\circ}} {2 \lambda} \left( d _ {A} - d _ {D} \right) + \frac {d _ {A} + d _ {D}} {2} \end{align} .\]

La última expresión proviene de la definición de la energía de reorganización (\(\lambda\)), que es la energía a disipar en la superficie aceptora si el electrón se transfiere a\(d_D\),

\[\begin{align} \lambda & = G _ {A} \left( d _ {D} \right) - G _ {A} \left( d _ {A} \right) \\ & = \frac {1} {2} m \omega _ {0}^{2} \left( d _ {D} - d _ {A} \right)^{2} \label{14.59} \end{align} \]

Entonces, la barrera de energía libre para la transferencia\(\Delta G^{\dagger}\) es

\[\begin{aligned} \Delta G^{\dagger} & = G _ {D} \left( d _ {C} \right) - G _ {D} \left( d _ {D} \right) \\ & = \frac {1} {2} m \omega _ {0}^{2} \left( d _ {C} - d _ {D} \right)^{2} \\ & = \frac {1} {4 \lambda} \left[ \Delta G^{\circ} + \lambda \right]^{2} \end{aligned}.\]

Entonces la constante de velocidad de Arrhenius es para la transferencia de electrones a través de cruce de barrera activada es

\[k _ {E T} = A \exp \left[ \frac {- \left( \Delta G^{\circ} + \lambda \right)^{2}} {4 \lambda k T} \right] \label{14.60}\]

Esta curva reproduce cualitativamente observaciones de una tasa máxima de transferencia de electrones bajo las condiciones\(- \Delta G^{\circ} = \lambda\), lo que ocurre en el caso sin barreras cuando la parábola aceptora cruza el mínimo de energía del estado donante.

Esperamos que podamos describir con mayor precisión la transferencia de electrones no adiabática utilizando el DHO o Energy Gap Hamiltonian, lo que incluirá la posibilidad de tunelizar a través de la barrera cuando las funciones de onda donador y aceptor se superpongan. Comenzamos por escribir las tasas de transferencia en términos de la energía potencial como antes. Reconocemos que cuando calculamos las tasas de transferencia promediadas térmicamente, esto equivale a describir las superficies de energía libre diabática. El hamiltoniano es

\[H = H _ {0} + V \label{14.61}\]

con

\[H _ {0} = | D \rangle H _ {D} \langle D | + | A \rangle H _ {A} \langle A | \label{14.62}\]

Aquí\(| D \rangle\) y\(| A \rangle\) se refieren al potencial donde el electrón está ya sea en el donante o aceptor, respectivamente. También recuerda que\(| D \rangle\) se refiere a los estados vibrónicos

\[| D \rangle = | d , n \rangle.\]

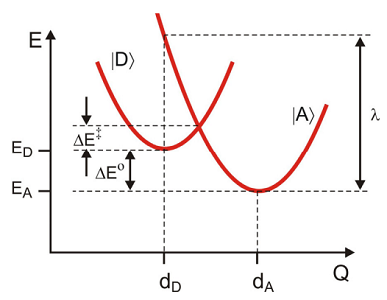
Estos se representan a través del mismo potencial armónico, desplazados uno del otro verticalmente en energía por

\[\Delta E = E _ {A} - E _ {D}\]

y horizontalmente a lo largo de las coordenadas de reacción\(q\):

\[\begin{align} H _ {D} &= | d \rangle E _ {D} \langle d | + H _ {d} \\[4pt] H _ {A} &= | a \rangle E _ {A} \langle a | + H _ {a} \label{14.63} \end{align} \]

\[\left.\begin{aligned} H _ {d} & = \hbar \omega _ {0} \left( p^{2} + \left( q - d _ {D} \right)^{2} \right) \\ H _ {a} & = \hbar \omega _ {0} \left( p^{2} + \left( q - d _ {A} \right)^{2} \right) \end{aligned} \right. \label{14.64}\]

Aquí estamos usando variables reducidas para los momentos, coordenadas y desplazamientos del oscilador armónico. Las superficies diabáticas se pueden expresar como estados de producto en las configuraciones electrónica y nuclear:\(| D \rangle = | d , n \rangle\). A la interacción entre las superficies se le asigna un acoplamiento\(J\)

\[V = J [ | d \rangle \langle a | + | a \rangle \langle d | ] \label{14.65}\]

Hemos realizado la aproximación del Condón, implicando que el elemento de la matriz de transferencia que describe la interacción electrónica no tiene dependencia de la coordenada nuclear. Por lo general, se espera que este acoplamiento electrónico disminuya exponencialmente con la separación entre orbitales donador y aceptor;

\[J = J _ {0} \exp \left( - \beta _ {E} \left( R - R _ {0} \right) \right) \label{14.66}\]

Aquí\(\beta_E\) está el parámetro que rige la dependencia de distancia de la integral de superposición. Para nuestros propósitos, aunque esto es una función de la separación donante-aceptor (R), tomamos esto para variar lentamente sobre los desplazamientos aquí investigados, y por lo tanto ser independientes de la coordenada nuclear (\(Q\)).

Marcus evaluó la expresión de la teoría de perturbación para la tasa de transferencia mediante el cálculo de los factores Franck-Condon para la superposición de superficies donadoras y aceptoras, de manera similar a nuestro tratamiento del espectro de absorción electrónica DHO. De igual manera, podemos proceder a calcular las tasas de transferencia de electrones utilizando la expresión de la Regla de Oro para la transferencia de amplitud entre dos estados

\[w _ {k \ell} = \frac {1} {\hbar^{2}} \int _ {- \infty}^{+ \infty} d t \left\langle V _ {I} (t) V _ {I} ( 0 ) \right\rangle \label{14.67}\]

Usando

\[V _ {I} (t) = e^{i H _ {0} t / \hbar} V e^{- i H _ {0} t / \hbar},\]

escribimos la tasa de transferencia de electrones en forma de autoestado DHO como

\[w _ {E T} = \frac {| J |^{2}} {\hbar^{2}} \int _ {- \infty}^{+ \infty} d t e^{- i \Delta E t / \hbar} F (t) \label{14.68}\]

donde

\[F (t) = \left\langle e^{i H _ {d} t / h} e^{- i H _ {a} t / h} \right\rangle \label{14.69}\]

Esta forma enfatiza que la velocidad de transferencia de electrones se rige por la superposición de paquetes de ondas vibracionales en las superficies de energía potencial donante y aceptor.

Alternativamente, podemos lanzar esto en la forma de la Brecha de Energía Hamiltoniana. Esto lleva consigo una imagen dinámica del evento de transferencia de electrones. La energía de los dos estados tiene energías dependientes del tiempo (fluctuantes) como resultado de su interacción con el entorno. Ocasionalmente la energía de los estados donante y aceptor coinciden que es la brecha energética entre ellos es cero. En este punto la transferencia se vuelve eficiente. Al integrar sobre la función de correlación para estas fluctuaciones de brecha de energía, caracterizamos las estadísticas para el cruce de barrera y, por lo tanto, la transferencia directa de electrones.

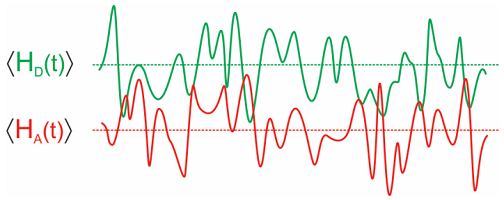
Similar a antes, definimos una brecha de energía donante-aceptor hamiltoniana

\[H _ {A D} = H _ {A} - H _ {D} \label{14.70}\]

que nos permite escribir

\[F (t) = \left\langle \exp _ {+} \left[ - \frac {i} {\hbar} \int _ {0}^{t} d t^{\prime} H _ {A D} \left( t^{\prime} \right) \right] \right\rangle \label{14.71}\]

y

\[H _ {A D} (t) = e^{i H _ {d} t / \hbar} H _ {A D} e^{- i H _ {d} t / \hbar} \label{14.72}\]

Estas expresiones y aplicación del cumulante expansio n a la ecuación nos permiten expresar la tasa de transferencia en términos de la función de lineshape y función de correlación

\[F (t) = \exp \left[ \frac {- i} {\hbar} \left\langle H _ {A D} \right\rangle t - g (t) \right] \label{14.73}\]

\[g (t) = \int _ {0}^{t} d \tau _ {2} \int _ {0}^{\tau _ {2}} d \tau _ {1} C _ {A D} \left( \tau _ {2} - \tau _ {1} \right) \label{14.74}\]

\[C _ {A D} (t) = \frac {1} {\hbar^{2}} \left\langle \delta H _ {A D} (t) \delta H _ {A D} ( 0 ) \right\rangle \label{14.75}\]

\[\left\langle H _ {A D} \right\rangle = \lambda \label{14.76}\]

La función lineshape también se puede escribir como una suma de muchas coordenadas nucleares acopladas,\(q_{\alpha}\). Esta expresión se aplica comúnmente a las contribuciones vibrónicas (capa interna) a la velocidad de transferencia:

\[\begin{align} g (t) &= - \sum _ {\alpha} \left( d _ {\alpha}^{A} - d _ {\alpha}^{D} \right)^{2} \left[ \left( \overline {n} _ {\alpha} + 1 \right) \left( e^{- i \omega _ {\alpha} t} - 1 + i \omega _ {0} t \right) + \overline {n} _ {\alpha} \left( e^{i \omega _ {a} t} - 1 - i \omega _ {0} t \right) \right] \\[4pt] &= - \sum _ {\alpha} \left( d _ {\alpha}^{A} - d _ {\alpha}^{D} \right)^{2} \left[ \operatorname {coth} \left( \beta \hbar \omega _ {\alpha} / 2 \right) \left( \cos \omega _ {\alpha} t - 1 \right) - i \left( \sin \omega _ {\alpha} t - \omega _ {\alpha} t \right) \right] \label{14.77} \end{align}\]

Sustituir la expresión por un modo armónico único en la expresión de velocidad de regla de oro da

\[\begin{align} w _ {E T} &= \frac {| J |^{2}} {\hbar^{2}} \int _ {- \infty}^{+ \infty} d t e^{- i \Delta E t / \hbar - g (t)} \label{4.78} \\[4pt] &= \frac {| J |^{2}} {\hbar^{2}} \int _ {- \infty}^{+ \infty} d t e^{- i ( \Delta E + \lambda ) t / \hbar} \exp \left[ D \left( \operatorname {coth} \left( \beta \hbar \omega _ {0} / 2 \right) \left( \cos \omega _ {0} t - 1 \right) - i \sin \omega _ {0} t \right) \right] \label{14.78} \end{align}\]

donde

\[D = \left( d _ {A} - d _ {D} \right)^{2} \label{14.79}\]

Esta expresión es muy similar a la que evaluamos para la forma de línea de absorción del modelo de Oscilador Armónico Desplazado. Se da una evaluación detallada de esta tasa de transferencia mediada vibrónicamente en Jortner.

Para tener una idea de la\(k\) dependencia de\(q\), podemos mirar el límite clásico\(\hbar \omega \ll k T\). Esto corresponde al caso en el que se está describiendo el caso de un efecto de “modo solvente” o “esfera externa” de baja frecuencia sobre la transferencia de electrones. Ahora, descuidamos la parte imaginaria\(g(t)\) y tomamos el límite

\[\operatorname {coth} ( \beta \hbar \omega / 2 ) \rightarrow 2 / \beta \hbar \omega\]

por lo

\[w _ {E T} = \frac {| J |^{2}} {\hbar^{2}} \int _ {- \infty}^{+ \infty} d t e^{- i ( \Delta E + \lambda ) t} \exp \left( - \left( \frac {2 D k _ {B} T} {\hbar \omega _ {0}} \right) \left( 1 - \cos \omega _ {0} t \right) \right) \label{14.80}\]

Tenga en cuenta que el límite de temperatura alta también significa el límite de baja frecuencia para\(\omega _ {0}\). Esto significa que podemos ampliar

\[\cos \omega _ {0} t \approx 1 - \left( \omega _ {0} t \right)^{2} / 2,\]

y encuentra

\[w _ {E T} = \frac {| J |^{2}} {\hbar} \sqrt {\frac {\pi} {\lambda k T}} \exp \left[ \frac {- ( \Delta E + \lambda )^{2}} {4 \lambda k T} \right] \label{14.81}\]

donde\(\lambda = D \hbar \omega _ {0}\). Tenga en cuenta que la barrera de activación\(\Delta E^{\dagger}\) para osciladores armónicos desplazados es\(\Delta E^{\dagger} = \Delta E + \lambda\). Para una velocidad promediada térmicamente es apropiado asociar la brecha de energía promedio con la energía libre estándar de reacción,

\[\left\langle H _ {A} - H _ {D} \right\rangle - \lambda = \Delta G^{0}.\]

Por lo tanto, esta expresión es equivalente al resultado clásico de Marcus para la tasa de transferencia de electrones

\[k _ {E T} = A \exp \left[ \frac {- \left( \Delta G^{o} + \lambda \right)^{2}} {4 \lambda k T} \right] \label{14.82}\]

donde el pre-exponencial es

\[A = 2 \pi | J |^{2} / \hbar \sqrt {4 \pi \lambda k T} \label{14.83}\]

Esta expresión muestra el comportamiento no lineal esperado para la dependencia de la velocidad de transferencia de electrones de la fuerza impulsora para la transferencia hacia adelante, es decir, la energía libre de reacción. Esto es inusual porque generalmente pensamos en términos de una relación lineal de energía libre entre la velocidad de una reacción y la constante de equilibrio:

\[\ln k \propto \ln K _ {e q}.\]

Esto lleva a pensar que la tasa debería aumentar a medida que aumentamos la energía libre de conducción para la reacción\(-\Delta G^{0}\). Este comportamiento sólo se mantiene para una pequeña región en\(\Delta G^{0}\). En cambio, eq. muestra que la tasa ET aumentará con\(-\Delta G^{0}\), hasta que se observe una tasa máxima para\(-\Delta G^{0}=\lambda\) y la tasa luego disminuya. Esta disminución de k con incremento\(-\Delta G^{0}\) se conoce como el “régimen invertido”. El comportamiento invertido significa que se necesita excitación vibracional extra para alcanzar el cruce de la curva a medida que se baja el pozo aceptor. El comportamiento de alta temperatura para el acoplamiento a un modo de baja frecuencia\(\left(100 \mathrm{~cm}^{-1} \text {at } 300 \mathrm{~K}\right)\) se muestra a la derecha, además de una caricatura que indica el desplazamiento de la curva cruzando\(\Delta G^{0}\) en incremento.

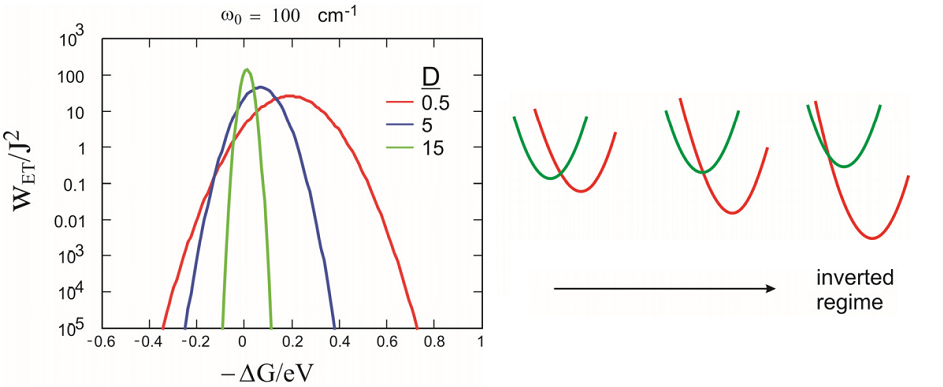
Particularmente en ET intramolecular, es común que se quiera explicar por separado la influencia de una vibración intramolecular de alta frecuencia (ET de esfera interna) que no está en el límite clásico que se aplica a la respuesta solvente clásica de baja frecuencia. Si se agrega un modo adicional de frecuencia\(\omega _ {0}\) y una tasa en forma de Ecuación\ ref {14.81} al modo de baja frecuencia, Jortner ha dado una expresión para la tasa como:

\[w _ {E T} = \frac {| J |^{2}} {\hbar} \sqrt {\frac {\pi} {\lambda _ {0} k T}} \sum _ {j = 0}^{\infty} \left( \frac {e^{- D}} {j !} D^{j} \right) \exp \left[ \frac {- \left( \Delta G^{o} + \lambda _ {0} + j \hbar \omega _ {0} \right)^{2}} {4 \lambda _ {0} k T} \right] \label{14.84}\]

Aquí\(\lambda _ {0}\) está la energía de reorganización de solvatación. Para este caso, existe el mismo régimen invertido; aunque ya\(\Delta G^{0}\) no existe la simple dependencia gaussiana de\(k\) on. La asimetría aquí existe porque la tunelización ve una barrera más estrecha en el régimen invertido que en el régimen normal. Ejemplos de las tasas obtenidas con eq. se trazan en la siguiente figura (T= 300 K).

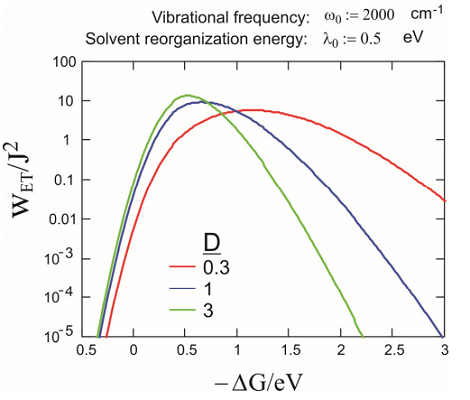
Al igual que con la espectroscopia electrónica, una manera más general y efectiva de dar cuenta de los movimientos nucleares que median en el proceso de transferencia de electrones es describir la densidad ponderada de acoplamiento de los estados como una densidad espectral. Luego podemos usar el acoplamiento a un baño armónico para describir contribuciones solventes y/o vibracionales de forma arbitraria al evento de transferencia usando

\[g (t) = \int _ {0}^{\infty} d \omega\, \rho ( \omega ) \left[ \operatorname {coth} \left( \frac {\beta \hbar \omega} {2} \right) ( 1 - \cos \omega t ) + i ( \sin \omega t - \omega t ) \right] \label{14.85}\]

Lecturas

1. Barbara, P. F.; Meyer, T. J.; Ratner, M. A., Temas contemporáneos en la investigación de transferencia de electrones. J. Phys. Chem. 1996, 100, 13148-13168, y referencias dentro.
2. Georgievskii, Y.; Hsu, C.-P.; Marcus, R. A., Respuesta lineal en teoría de reacciones de transferencia de electrones como alternativa al modelo de oscilador armónico molecular. La Revista de Física Química 1999, 110, 5307-5317.
3. Jortner, J., La energía de activación dependiente de la temperatura para la transferencia de electrones entre moléculas biológicas. Revista de Física Química 1976, 64, 4860-4867.
4. Marcus, R. A.; Sutin, N., Transferencias de electrones en química y biología. Biochimica et Biophysica Acta (BBA) - Opiniones sobre Bioenergética 1985, 811, 265-322.
5. Nitzan, A., Dinámica Química en Fases Condensadas. Oxford University Press: Nueva York, 2006; Cap. 10