16.1: Relajación Vibracional

Aquí queremos abordar cómo el exceso de energía vibracional sufre una relajación energética irreversible como resultado de interacciones con otros grados de libertad intra e intermoleculares. ¿Por qué es importante este proceso? Es el proceso fundamental por el cual se termalizan los estados de no equilibrio. Como químicos, esto juega un papel particularmente importante en las reacciones químicas, donde la relajación vibratoria eficiente de una especie activada es importante para estabilizar el producto y no permitir que se vuelva a cruzar al pozo reactivo. Además, el raro evento de activación para reacciones químicas es similar al reverso de este proceso. Aunque veremos específicamente los acoplamientos vibracionales y la relajación, los principios son los mismos para la relajación electrónica de la población a través del acoplamiento electrónico-fonón y la relajación espina - celosía.

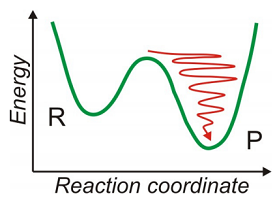
Para una molécula aislada con pocas coordenadas vibracionales, un estado vibracional excitado debe relajarse interactuando con las vibraciones internas restantes o los grados de libertad rotacional y traslacional. Si se debe disipar mucha energía, la relajación radiativa puede ser más probable. En la fase condensada, la relajación suele estar mediada por las interacciones con el ambiente, por ejemplo, el disolvente o la red. El solvente o celosía forma un continuo de movimientos intermoleculares que pueden absorber la energía de la relajación vibracional. Quantum mecánicamente esto significa que la relajación vibracional (la aniquilación de un cuántico vibracional) conduce a la excitación del movimiento solvente o reticular (creación de una vibración intermolecular que aumenta la ocupación de estados mentirosos superiores).

Para las moléculas poliatómicas es común pensar en la relajación energética de estados vibracionales altos (\(k T \ll \hbar \omega _ {0}\)) en términos de redistribución de energía en cascada a través de modos acoplados de la molécula y su entorno que conducen finalmente al equilibrio térmico. Buscamos formas de describir estos procesos de relajación altamente no equilibrados en sistemas cuánticos.

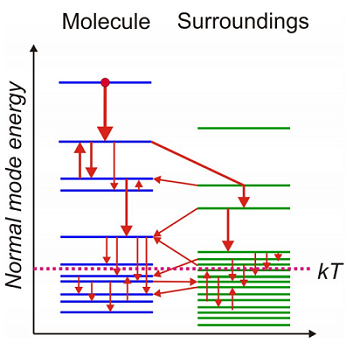
La relajación vibratoria clásica refleja el entorno ejerciendo una fricción sobre la coordenada vibratoria, lo que amortigua su amplitud y calienta la muestra. Hemos visto que una ecuación de Langevin para un oscilador que experimenta una fuerza fluctuante\(f(t)\) describe tal proceso:

\[\ddot {Q} (t) + \omega _ {0}^{2} Q^{2} - \gamma \dot {Q} = f (t) / m \label{15.1}\]

Esta ecuación asigna una tasa de amortiguación fenomenológica\(\gamma\) a la relajación vibratoria que deseamos describir. Sin embargo, sabemos que en el límite de tiempo largo, el sistema debe termalizarse y la disipación de energía está relacionada con las fluctuaciones del ambiente a través de la clásica relación fluctuación-disipación. Específicamente,

\[\langle f (t) f ( 0 ) \rangle = 2 m \gamma k _ {B} T \delta (t) \label{15.2}\]

Descripciones clásicas más generales relacionan las tasas de relajación vibracional con la función de correlación para las fuerzas fluctuantes que actúan sobre la coordenada excitada.

En estas imágenes clásicas, la relajación eficiente requiere una coincidencia de frecuencias entre el período vibratorio del oscilador excitado y el espectro de fluctuación del ambiente. Dado que estas fluctuaciones están dominadas por movimientos son de la escala de energía de\(k_BT\), tales modelos no funcionan de manera efectiva para vibraciones de alta frecuencia cuya frecuencia\(\omega \gg k_BT/\hbar\). Nos gustaría desarrollar un modelo cuántico que permita estos procesos y comprender la correspondencia entre estas imágenes clásicas y la relajación cuántica.

Tratemos el problema de un sistema vibratorio\(H_S\) que se relaja a través de un acoplamiento débil\(V\) a un continuo de estados de baño\(H_B\) utilizando la teoría de la perturbación. Los autoestados de\(H_S\) son\(| a \rangle\) y los de\(H_B\) son\(| \alpha \rangle\). Aunque nuestro tratamiento perturbador anterior no satisfizo la conservación de energía, aquí podemos cuidarlo tratando explícitamente los estados de baño.

\[\begin{align} H &= H _ {0} + V \label{15.3} \\[4pt] H _ {0} &= H _ {S} + H _ {B} \label{15.4} \end{align}\]

con

\[\begin{align} H _ {S} &= | a \rangle E _ {a} \langle a | + | b \rangle E _ {b} \langle b | \label{15.5} \\[4pt] H _ {B} &= \sum _ {\alpha} | \alpha \rangle E _ {\alpha} \langle \alpha | \label{15.6} \\[4pt] H _ {0} | a \alpha \rangle &= \left( E _ {a} + E _ {\alpha} \right) | a \alpha \rangle \label{15.7} \end{align}\]

Describiremos las transiciones de un estado inicial\(| i \rangle = | a \alpha \rangle\) con energía\(E _ {a} + E _ {\alpha}\) a un estado final\(| f \rangle = | b \beta \rangle\) con energía\(E _ {b} + E _ {\beta}\). Dado que esperamos que la conservación de energía se mantenga, esto sin duda requiere que un cambio en los estados del sistema requerirá un cambio igual y opuesto de energía en el baño.

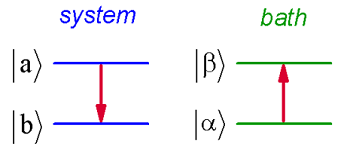
Inicialmente, tomamos\(p_a=1\) y\(p_b=0\). Si el potencial de interacción es\(V\), la regla de oro de Fermi dice que la transición de\(| i \rangle\) a\(| f \rangle\) viene dada por

\[\begin{align} k _ {f i} &= \frac {2 \pi} {\hbar} \sum _ {i , f} p _ {i} | \langle i | V | f \rangle |^{2} \delta \left( E _ {f} - E _ {i} \right) \label{15.8} \\[4pt] &= \frac {2 \pi} {\hbar} \sum _ {a , \alpha , b , \beta} p _ {a , \alpha} | \langle a \alpha | V | b \beta \rangle |^{2} \delta \left( \left( E _ {b} + E _ {\beta} \right) - \left( E _ {a} + E _ {\alpha} \right) \right) \\[4pt] &= \frac {1} {\hbar^{2}} \int _ {- \infty}^{+ \infty} d t \sum _ {a , \alpha \atop b , \beta} p _ {a , \alpha} \langle a \alpha | V | b \beta \rangle \langle b \beta | V | a \alpha \rangle e^{- i \left( E _ {b} - E _ {a} \right) + \left( E _ {\beta} - E _ {\alpha} \right) ) t / \hbar} \label{15.10} \end{align}\]

La ecuación\ ref {15.10} es solo una reformulación de la versión de dominio de tiempo de la ecuación\ ref {15.8}

\[k _ {f _ {f}} = \frac {1} {\hbar^{2}} \int _ {- \infty}^{+ \infty} d t \langle V (t) V ( 0 ) \rangle \label{15.11}\]

con

\[V (t) = e^{i H _ {0} t} V e^{- i H _ {0} t} \label{15.12}\]

Ahora, el elemento matriz implica tanto la evaluación tanto en el sistema como en el estado de baño, pero si escribimos esto en términos de un elemento de matriz en la coordenada del sistema\(V _ {a b} = \langle a | V | b \rangle\):

\[\langle a \alpha | V | b \beta \rangle = \left\langle \alpha \left| V _ {a b} \right| \beta \right\rangle \label{15.13}\]

Entonces podemos escribir la tasa como

\[\begin{align} k_{b a} &=\frac{1}{\hbar^{2}} \int_{-\infty}^{+\infty} d t \sum_{\alpha, \beta} p_{\alpha}\left\langle\alpha\left|e^{+i E_{\alpha} t} V_{a b} e^{-i E_{\beta} t}\right| \beta\right\rangle\left\langle\beta\left|V_{b a}\right| \alpha\right\rangle e^{-i \omega_{b a} t} \label{15.14} \\[4pt] &=\frac{1}{\hbar^{2}} \int_{-\infty}^{+\infty} d t\left\langle V_{a b}(t) V_{b a}(0)\right\rangle_{B} e^{-i \omega_{b a} t} \label{15.15} \end{align}\]

\[V _ {a b} (t) = e^{i H _ {B} t} V _ {a b} e^{- i H _ {B} t} \label{15.16}\]

La ecuación\ ref {15.15} dice que la tasa de relajación está determinada por una función de correlación

\[C _ {b a} (t) = \left\langle V _ {a b} (t) V _ {b a} ( 0 ) \right\rangle \label{15.17}\]

que describe los cambios dependientes del tiempo en el acoplamiento entre\(b\) y\(a\). La dependencia temporal de la interacción surge de la interacción con el baño; de ahí su evolución temporal bajo\(H_B\). El subíndice\(\langle \cdots \rangle _ {B}\) significa un promedio térmico de equilibrio sobre los estados de baño

\[\langle \cdots \rangle _ {B} = \sum _ {\alpha} p _ {\alpha} \langle \alpha | \cdots | \alpha \rangle \label{15.18}\]

Tenga en cuenta también que la Ecuación\ ref {15.15} es similar pero no es una transformada de Fourier del todo. Esta expresión dice que la tasa de relajación viene dada por la transformada de Fourier de la función de correlación para el acoplamiento fluctuante evaluado en la brecha de energía entre los estados de estado inicial y final.

Alternativamente, podríamos pensar en la velocidad en términos de una densidad espectral de acoplamiento vibracional, y la velocidad viene dada por su magnitud en la brecha de energía del sistema\(\omega _ {b a}\).

\[k _ {b a} = \frac {1} {\hbar^{2}} \tilde {C} _ {b a} \left( \omega _ {a b} \right) \label{15.19}\]

donde la representación espectral\(\tilde {C} _ {b a} \left( \omega _ {\omega b} \right)\) se define como la transformada de Fourier de\(C _ {b a} (t)\).

Vibración acoplada a un baño armónico

Para evaluar estas expresiones, comencemos por considerar el caso específico de una vibración del sistema acoplada a un baño armónico, que describiremos por una densidad espectral. Imagina que preparamos el sistema en un estado vibracional excitado en\(v=|1\rangle\) y queremos describir la relajación\(v=|0\rangle\).

\[H _ {S} = \hbar \omega _ {0} \left( P^{2} + Q^{2} \right) \label{15.20}\]

\[H _ {B} = \sum _ {\alpha} \hbar \omega _ {\alpha} \left( p _ {\alpha}^{2} + q _ {\alpha}^{2} \right) = \sum _ {\alpha} \hbar \omega _ {\alpha} \left( a _ {\alpha}^{\dagger} a _ {\alpha} + \frac {1} {2} \right) \label{15.21}\]

Tomaremos que la interacción sistema-baño sea lineal en las coordenadas del baño:

\[V = H _ {S B} = \sum _ {\alpha} c _ {\alpha} Q q _ {\alpha} \label{15.22}\]

Aquí\(\mathcal {C} \alpha\) hay una constante de acoplamiento que describe la fuerza de la interacción entre el sistema y el modo de baño\(\alpha\). Tenga en cuenta, que esta forma sugiere que la vibración del sistema es un modo local que interactúa con un conjunto de vibraciones normales del baño.

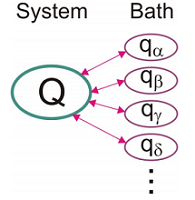
Para el caso de relajación cuántica única de\(| a \rangle = | 1 \rangle\) a\(b = | 0 \rangle\), podemos escribir el elemento de la matriz de acoplamiento como

\[V _ {b a} = \sum _ {\alpha} \xi _ {a b , \alpha} \left( a _ {\alpha}^{\dagger} + a _ {\alpha} \right) \label{15.23}\]

donde

\[\xi _ {a b , \alpha} = c _ {\alpha} \frac {\sqrt {m _ {\varrho} m _ {q} \omega _ {0} \omega _ {\alpha}}} {2 \hbar} \langle b | Q | a \rangle \label{15.24}\]

Nota

Nótese que estamos utilizando una propiedad de equilibrio, la función de correlación de acoplamiento, para describir un proceso de no equilibrio, la relajación de un estado excitado. Subyacentes a la validez de las expresiones están los principios de respuesta lineal. En la práctica esto implica también una separación en escala de tiempo entre el equilibrio del baño y la relajación del estado del sistema. La función de correlación del baño debe funcionar bien si se ha equilibrado rápidamente, aunque el sistema no lo haya hecho. Una instancia en la que esto funcionaría bien es la espectroscopia electrónica, donde la relajación y la termalización en el estado excitado ocurren en escalas de tiempo de picosegundos, mientras que la relajación electrónica de la población es en escalas de tiempo de nanosegundos.

Aquí\(\langle b | Q | a \rangle\) se toma el elemento matriz en la evaluación\(\xi _ {a b , \alpha}\). Evaluar la ecuación\ ref {15.17} es ahora casi lo mismo que los problemas que hemos tenido anteriormente:

\[\begin{align} \left\langle V _ {a b} (t) V _ {b a} ( 0 ) \right\rangle _ {B} &= \left\langle e^{i H _ {B} t} V _ {a b} e^{- i H _ {B} t} V _ {b a} \right\rangle _ {B} \\[4pt] &= \sum _ {\alpha} \xi _ {\alpha}^{2} \left[ \left( \overline {n} _ {\alpha} + 1 \right) e^{- i \omega _ {\alpha} t} + \overline {n} _ {\alpha} e^{+ i \omega _ {\alpha} t} \right] \label{15.25} \end{align}\]

aquí\(\overline {n} _ {\alpha} = \left( e^{\beta \hbar \omega _ {\alpha}} - 1 \right)^{- 1}\) está el número de ocupación promediado térmicamente del modo de baño en\(\omega_{\alpha}\). Al evaluar esto aprovechamos las relaciones que hemos utilizado antes

\[\overline {n} _ {\alpha} = \left( e^{\beta \hbar \omega _ {\alpha}} - 1 \right)^{- 1} \label{15.26}\]

\[\left. \begin{array} {l} {\left\langle a _ {\alpha} a _ {\alpha}^{\dagger} \right\rangle = \overline {n} _ {\alpha} + 1} \\ {\left\langle a _ {\alpha}^{\dagger} a _ {\alpha} \right\rangle = \overline {n} _ {\alpha}} \end{array} \right. \label{15.27}\]

Entonces, ahora por transformación de Fourier (Ecuación\ ref {15.25}) tenemos la tasa como

\[k _ {b a} = \frac {1} {\hbar^{2}} \sum _ {\alpha} \left[ \xi _ {\alpha} \right] _ {a b}^{2} \left[ \left( \overline {n} _ {\alpha} + 1 \right) \delta \left( \omega _ {b a} + \omega _ {\alpha} \right) + \overline {n} _ {\alpha} \delta \left( \omega _ {b a} - \omega _ {\alpha} \right) \right] \label{15.28}\]

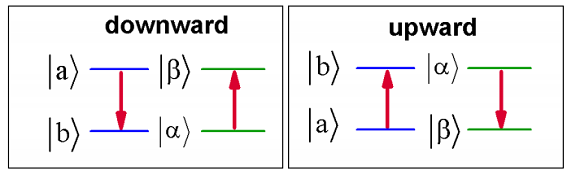
Esta expresión describe dos procesos de relajación que dependen de la temperatura. El primero está permitido en\(T = 0\, K\) y es obedece\(- \omega _ {b a} = \omega _ {\alpha}\). Esto implica eso\( E _ {a} > E _ {b} \), y que una pérdida de energía en el sistema se equilibra con una subida igual en la energía del baño. Eso es\(| \beta \rangle = | \alpha + 1 \rangle\). El segundo término sólo está permitido para temperaturas elevadas. Describe la relajación del sistema por transferencia a un estado energético superior\(E _ {b} > E _ {a}\), con una disminución concertada de la energía del baño (\(| \beta \rangle = | \alpha - 1 \rangle\)). Naturalmente, este proceso se desvanece si no hay energía térmica en el baño.

Nota

Existe una analogía exacta entre este problema y la interacción de la materia con un campo de radiación cuántica. El potencial de interacción es en cambio un potencial de vector cuántico y el baño es el campo de fotones de diferentes modos electromagnéticos. La ecuación\ ref {15.28} describe tiene dos términos que describen los procesos de emisión y absorción. El término principal describe la posibilidad de emisión espontánea, donde un sistema material puede relajarse en ausencia de luz emitiendo un fotón a la misma frecuencia.

Para modelar con mayor precisión la relajación debido a un continuo de modos, podemos reemplazar la suma explícita sobre los estados de baño con una integral sobre una densidad de estados de baño\(W\)

\[k _ {b a} = \frac {1} {\hbar^{2}} \int d \omega _ {\alpha} W \left( \omega _ {\alpha} \right) \xi _ {b a}^{2} \left( \omega _ {\alpha} \right) \left[ \left( \overline {n} \left( \omega _ {\alpha} \right) + 1 \right) \delta \left( \omega _ {b a} + \omega _ {\alpha} \right) + \overline {n} \left( \omega _ {\alpha} \right) \delta \left( \omega _ {b a} - \omega _ {\alpha} \right) \right] \label{15.29}\]

También podemos definir una densidad espectral, que es la densidad de estados ponderada por acoplamiento vibracional:

\[\rho \left( \omega _ {\alpha} \right) \equiv W \left( \omega _ {\alpha} \right) \xi _ {b a}^{\mathcal {E}} \left( \omega _ {\alpha} \right) \label{15.30}\]

Entonces la tasa de relajación es:

\[\left.\begin{aligned} k _ {b a} & = \frac {1} {\hbar^{2}} \int d \omega _ {\alpha} W \left( \omega _ {\alpha} \right) \xi _ {b a}^{2} \left( \omega _ {\alpha} \right) \left[ \left( \overline {n} \left( \omega _ {\alpha} \right) + 1 \right) \delta \left( \omega _ {b a} + \omega _ {\alpha} \right) + \overline {n} \left( \omega _ {\alpha} \right) \delta \left( \omega _ {b a} - \omega _ {\alpha} \right) \right] \\ & = \frac {1} {\hbar^{2}} \left[ \left( \overline {n} \left( \omega _ {b a} \right) + 1 \right) \rho _ {b a} \left( \omega _ {a b} \right) + \overline {n} \left( \omega _ {b a} \right) \rho _ {b a} \left( - \omega _ {a b} \right) \right] \end{aligned} \right. \label{15.31}\]

Vemos que la transformada de Fourier de la función de correlación de acoplamiento fluctuante, es equivalente a la densidad ponderada por acoplamiento de estados, que evaluamos en\(\omega _ {b a}\) o\(-\omega _ {b a}\) dependiendo de si estamos mirando transiciones hacia arriba o hacia abajo. Tenga en cuenta que\(\overline {n}\) todavía se refiere al número de ocupación para el baño, aunque se evalúa en la división de energía entre los estados del sistema inicial y final. La ecuación\ ref {15.31} es una expresión cuántica completa, y obedece al equilibrio detallado entre las tasas de transición ascendente y descendente entre dos estados:

\[k _ {b a} = \exp \left( - \beta \hbar \omega _ {a b} \right) k _ {a b} \label{15.32}\]

De nuestra descripción del sistema de dos niveles en un baño armónico, vemos que la relajación de alta frecuencia (\(k T < < \hbar \omega _ {0}\)) solo procede con la energía del sistema entrando en un modo del baño a la misma frecuencia, pero a frecuencias más bajas (\(k T \approx \hbar \omega _ {0}\)) esa energía puede fluir tanto hacia el baño como desde el baño hacia atrás en el sistema. Cuando la vibración tiene energías que se pueblan térmicamente en el baño, volvemos al cuadro clásico de una vibración en un ambiente fluctuante que puede disipar la energía de la vibración además de dar patadas que aumentan la energía de la vibración. Tenga en cuenta que en un esquema de relajación en cascada, a medida que uno se acerca a kT, la fracción de transiciones que aumentan la energía del sistema aumenta. También, señalar que el acoplamiento bi-lineal en la Ecuación\ ref {15.22} y utilizado en nuestro tratamiento de las fluctuaciones cuánticas puede asociarse con fluctuaciones del baño que inducen cambios en la energía (relajación) y desplazamientos de frecuencia (desfase).

Relajación multicuántica de moléculas poliatómicas

3 La relajación vibracional de moléculas poliatómicas en sólidos o en solución implica el acoplamiento anarmónico de energía entre las vibraciones internas de la molécula, también llamada IVR (redistribución interna de energía vibratoria). Las interacciones mecánicas entre múltiples modos de vibración de la molécula actúan para revolver rápidamente la energía depositada en una coordenada vibracional y conducir a un flujo de energía en cascada hacia el equilibrio.

Para este problema el acoplamiento bilineal anterior no captura el proceso de relajación adecuado. En cambio, podemos expresar la energía potencial molecular en términos de modos normales de vibración bien definidos para el sistema y el baño, y estos interactúan débilmente a través de pequeños términos anarmónicos en el potencial. Entonces podemos extender el enfoque perturbador anterior para incluir el efecto de múltiples vibraciones de aceptación del sistema o baño. Para un conjunto de coordenadas del sistema y del baño, la energía potencial para la interacción entre el sistema y el baño se puede ampliar como

\[V _ {S} + V _ {S B} = \frac {1} {2} \sum _ {a} \frac {\partial^{2} V} {\partial Q _ {a}^{2}} Q _ {a}^{2} + \frac {1} {6} \sum _ {a , \alpha , \beta} \frac {\partial^{3} V} {\partial Q _ {a} \partial q _ {\alpha} \partial q _ {\beta}} Q _ {a , b , \alpha} q _ {\beta} + \frac {1} {6} \sum _ {a , b , \alpha} \frac {\partial^{3} V} {\partial Q _ {a} \partial Q _ {b} \partial q _ {\alpha}} Q _ {a} Q _ {b} q _ {\alpha} \cdots \label{15.33}\]

Centrándose explícitamente en el primer término de expansión cúbica, para un oscilador de sistema:

\[V _ {S} + V _ {S B} = \frac {1} {2} m \Omega^{2} Q^{2} + V^{( 3 )} Q q _ {\alpha} q _ {\beta} \label{15.34}\]

Aquí, el potencial de interacción sistema-baño describe el caso de un acoplamiento anarmónico cúbico que implica una vibración del sistema\(Q\) interactuando débilmente con dos vibraciones del baño\(\frac {9} {2} \alpha\) y\(9 _ {\beta}\), así que eso\(\hbar \Omega \gg V^{( 3 )}\). La energía depositada en la vibración del sistema se disipará a las dos vibraciones del baño, un proceso de tres cuánticos. Los términos de expansión de orden superior describirían interacciones que involucran cuatro o más cuantos.

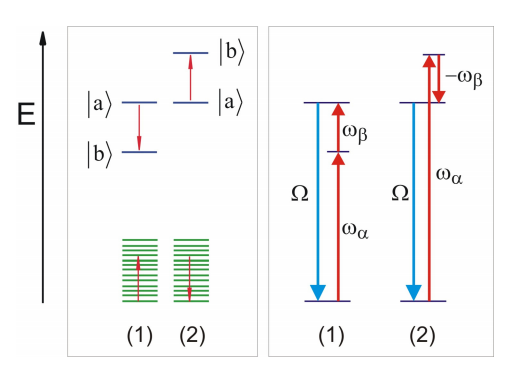
Trabajando específicamente con el ejemplo cúbico, podemos usar el modelo de baño armónico para calcular la tasa de relajación energética. Esta imagen es aplicable si un modo vibracional de frecuencia se\(\Omega\) relaja transfiriendo su energía a otra vibración cercana en energía (\(\infty _ {\alpha}\)), y la diferencia de energía\(\omega _ {\beta}\) se explica por un continuo de movimientos intermoleculares. Para este caso se puede mostrar

\[k _ {b a} = \frac {1} {\hbar^{2}} \left[ \left( \overline {n} \left( \omega _ {\alpha} \right) + 1 \right) \left( \overline {n} \left( \omega _ {\beta} \right) + 1 \right) \rho _ {b a} \left( \omega _ {a b} \right) + \left( \overline {n} \left( \omega _ {\alpha} \right) + 1 \right) \overline {n} \left( \omega _ {\beta} \right) \rho _ {b a} \left( \omega _ {a b} \right) \right] \label{15.35}\]

donde\(\rho ( \omega ) \equiv W ( \omega ) \left( V^{( 3 )} ( \omega ) \right)^{2}.\). Aquí hemos tomado,\(\Omega , \omega _ {\alpha} \gg \omega _ {\beta}\). Estos dos términos describen dos posibles vías de relajación, la primera en la que la aniquilación de un cuántico de\(\Omega\) conduce a una creación de un cuántico cada uno de\(\omega_{\alpha} \text { and } \omega_{\beta}\). El segundo término describe la disipación de energía mediante el acoplamiento a una vibración de mayor energía, siendo absorbida el exceso de energía del baño. La aniquilación de un cuántico de\(\Omega\) conduce a una creación de un cuántico de\(\omega_{\alpha}\) y la aniquilación de un cuántico de\(\omega_{\beta}\). Naturalmente este último término sólo se permite cuando hay suficiente energía térmica presente en el baño.

Cálculos de velocidad usando relajación vibratoria clásica

En general, nos gustaría una forma práctica de calcular las tasas de relajación, y calcular las funciones de correlación cuántica no es práctico. ¿Cómo utilizamos los cálculos clásicos para el baño, por ejemplo, a partir de una simulación clásica de dinámica molecular? ¿Hay alguna manera de obtener una tasa mecánica cuántica?

El primer problema es que la función de correlación cuántica es compleja\(C _ {a b}^{*} (t) = C _ {a b} ( - t )\) y la función de correlación clásica es real y uniforme\(C _ {C l} (t) = C _ {C l} ( - t )\). Para conectar estas dos funciones de correlación, se puede derivar un factor de corrección cuántica que permite predecir la función de correlación cuántica sobre la base de la clásica. Esto se basa en el supuesto de que a alta temperatura debería ser posible sustituir la función de correlación clásica con la parte real de la función de correlación cuántica

\[C _ {c} (t) \Rightarrow C _ {b n}^{\prime} (t) \label{15.36}\]

Para realizar este ajuste partimos de la expresión de dominio de frecuencia derivada de la expresión de balance detallado\(\tilde {C} ( - \omega ) = e^{- \beta \hbar \omega} \tilde {C} ( \omega )\)

\[\tilde {C} ( \omega ) = \frac {2} {1 + \exp ( - \beta \hbar \omega )} \tilde {C}^{\prime} ( \omega ) \label{15.37}\]

Aquí\(\tilde {C}^{\prime} ( \omega )\) se define como la transformada de Fourier de la parte real de la función de correlación cuántica. Entonces la tasa de relajación vibracional es

\[k _ {b a} = \frac {4} {\hbar^{2} \left( 1 + \exp \left( - \hbar \omega _ {b a} / k T \right) \right)} \int _ {0}^{\infty} d t e^{- i \omega _ {\omega a} t} \operatorname {Re} \left[ \left\langle V _ {a b} (t) V _ {b a} ( 0 ) \right\rangle \right] \label{15.38}\]

Ahora vamos a suponer que se puede reemplazar un cálculo clásico de la función de correlación aquí como en la Ecuación\ ref {15.36}. El término principal en el frente puede considerarse un “factor de corrección cuántica” que da cuenta del balance detallado de las tasas codificadas en la densidad espectral cuántica.

En la práctica, dicho cálculo podría hacerse con simulaciones de dinámica molecular. Aquí se tiene una caracterización explícita de las fuerzas intermoleculares que actuarían para amortiguar el modo vibratorio excitado. Se pueden calcular las interacciones sistema-baño expandiendo el potencial vibratorio del sistema en las coordenadas del baño

\[\left.\begin{aligned} V _ {S} + V _ {s B} & = V _ {0} + \sum _ {\alpha} \frac {\partial V^{\alpha}} {\partial Q} Q + \sum _ {\alpha} \frac {\partial^{2} V^{\alpha}} {\partial Q^{2}} Q^{2} + \cdots \\ & = V _ {0} + F Q + G Q^{2} + \cdots \end{aligned} \right. \label{15.39}\]

Aquí\(V^{\alpha}\) representa el potencial de una interacción de una coordenada solvente que actúa sobre la coordenada del sistema vibracional excitado\(Q\). El segundo término en esta expansión\(FQ\) depende linealmente de las\(\alpha\) coordenadas del sistema\(Q\) y del baño, y podemos usar la variación en este parámetro para calcular la función de correlación para el potencial de interacción fluctuante. ¡Tenga en cuenta que\(F\) es la fuerza sobre la que ejercen las moléculas\(Q\)! Así, la función de correlación clásica relevante para la relajación vibratoria es una función de correlación de fuerzas

\[C _ {C l} (t) = \langle F (t) F ( 0 ) \rangle \label{15.40}\]

\[k _ {C l} = \frac {1} {k T} \int _ {0}^{\infty} d t \cos \omega _ {b a} t \langle F (t) F ( 0 ) \rangle \label{15.41}\]

Lecturas

1. Egorov, S. A.; Rabani, E.; Berna, B. J., Procesos de relajación no radiativa en fases condensadas: baños cuánticos versus clásicos. J. Chem. Phys. 1999, 110, 5238-5248.
2. Kenkre, V. M.; Tokmakoff, A.; Fayer, M. D., Teoría de la relajación vibracional de moléculas poliatómicas en líquidos. The Journal of Chemical Physics 1994, 101, 10618.
3. Nitzan, A., Dinámica Química en Fases Condensadas. Oxford University Press: Nueva York, 2006; Capítulo 11.
4. Oxtoby, D. W., Relaxión poblacional vibracional en líquidos. Adv. Chem. Phys. 1981, 47, 487- 519.
5. Skinner, J. L., Aproximaciones semiclásicas a constantes de tasa de regla de oro. La Revista de Física Química 1997, 107, 8717-8718.
6. Slichter, C. P., Principios de Resonancia Magnética, con Ejemplos de Física de Estado Sólido. Harper & Row: Nueva York, 1963.