2.1: Respuesta, Relajación y Correlación

A principios del siglo XXI, la termodinámica de sistemas alejados del equilibrio sigue siendo poco entendida. Sin embargo, resulta que muchos fenómenos de no equilibrio pueden describirse bastante bien en términos de fluctuaciones de equilibrio; esto es especialmente cierto en sistemas cercanos al equilibrio\([1,2]\).

Al designar un sistema como “casi equilibrio”, queremos decir que el sistema está perturbado desde su estado de equilibrio por alguna fuerza externa dependiente del tiempo\(f(t)\). La fuerza externa es determinista, no aleatoria; ejemplos típicos incluyen fuerzas mecánicas y fuerzas debidas a un campo eléctrico o magnético aplicado. Esta fuerza aleja los valores de expectativa de algunos de los observables del sistema de sus valores de equilibrio. Por ejemplo, un típico observable\(A\) afectado por la fuerza externa podría ser la velocidad del sistema o su momento magnético. Si la respuesta de lo observable\(A\) a la fuerza externa\(f(t)\) satisface la propiedad de linealidad

\[\delta A(\lambda f(t), t)=\lambda \delta A(f(t), t)\]

donde\(\delta A=A-\langle A\rangle_{e q}\) y\(\lambda\) describe la fuerza de la fuerza, entonces llamamos el comportamiento dependiente del tiempo de\(A\) la respuesta lineal de\(A\) a la fuerza externa\(f(t)\). La propiedad de linealidad Eq. (2.1) implica que la forma de la curva de respuesta\(A\) vs\(t\) es independiente del valor de\(\lambda\) en el caso de respuesta lineal.

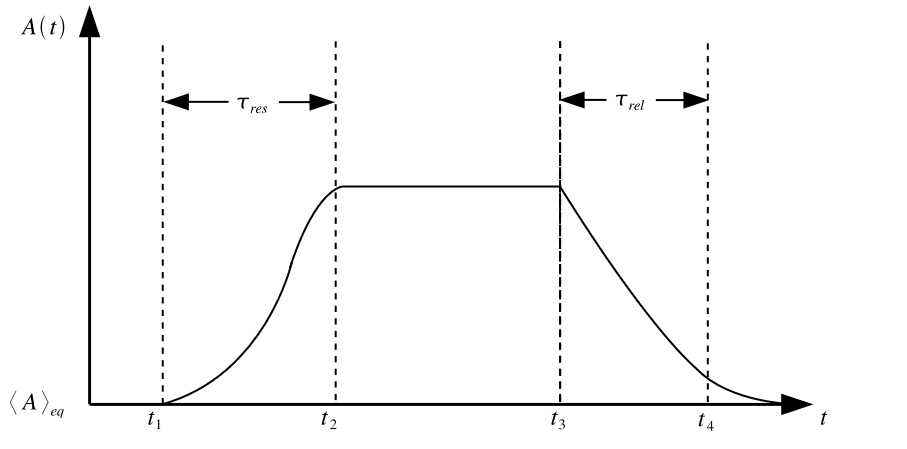
Después de lograr un estado estacionario de no equilibrio de corta duración (entre\(t_{2}\) y\(t_{3}\) en la Figura 2.1), se permite que el sistema se relaje de nuevo al equilibrio. Este proceso también se conoce como regresión. La respuesta lineal y la regresión de un sistema impulsado desde el equilibrio se describen en términos de la función de correlación temporal de lo observable\(A\), y así pasamos primero a la definición y propiedades de la función de correlación de tiempo\([3,4]\).

La función\(C_{A A}\left(t, t^{\prime}\right)\) de correlación temporal del observable\(A\) se define por

\[C_{A A}\left(t, t^{\prime}\right)=\left\langle A(t) A\left(t^{\prime}\right)\right\rangle=\frac{\operatorname{Tr}\left[A(t) A\left(t^{\prime}\right) \rho_{e q}\right]}{\operatorname{Tr}\left[\rho_{e q}\right]}\]

Aquí,\(\rho_{e q}\) denota la matriz de densidad de equilibrio del sistema; de ahí que el promedio denotado por\(\langle\rangle\) es el promedio conjunto. Esta función describe cómo se correlaciona el valor de\(A\) en\(t\) el tiempo con su

Figura 2.1: Respuesta, estado estacionario de no equilibrio y relajación

valor en el momento en\(t^{\prime} ;\) que a veces se le conoce como la función de autocorrelación de\(A\) para distinguirlo de las funciones de correlación entre\(A\) y otros observables.

Para un sistema que es invariante traslacional en el tiempo, a menudo elegimos por conveniencia establecer\(t^{\prime}=0\) y soltar el subíndice\(C_{A A}\), de modo que la función de correlación de tiempo se vuelva simplemente

\[C(t)=\langle A(t) A(0)\rangle\]

La función de correlación puede, en general, tomar valores complejos. Este resultado está en consonancia con nuestra comprensión fenomenológica de la mecánica cuántica de la siguiente manera. Para medir la función de correlación de una A observable, la cantidad A debe medirse dos veces (primero en el tiempo cero, luego nuevamente en el tiempo\(t\)). Sin embargo, la primera medición en\(t=0\) colapsa el sistema wavepacket, y el estado que habría sido exhibido por el sistema imperturbable en el momento\(t\) se vuelve irrecuperable.

Ahora identificamos algunas características y propiedades importantes de las funciones de correlación.

1. Todos los productos interiores\(\langle X \mid Y\rangle\) satisfacen la desigualdad Schwarz

\[|\langle X \mid Y\rangle|^{2} \leq\left\langle X^{2}\right\rangle\left\langle Y^{2}\right\rangle\]

Así la función de correlación para cualquier proceso de relajación tiene la propiedad

\[C^{2}(t)=|\langle A(t) \mid A(0)\rangle|^{2} \leq\left\langle A^{2}(t) A^{2}(0)\right\rangle \leq\left\langle A^{2}(0)\right\rangle^{2}=C^{2}(0)\]

La segunda desigualdad anterior surge del hecho de que\(A^{2}(t)<A^{2}(0)\) para los procesos de relajación cuando\(t>0\). De manera más concisa, la desigualdad de Schwarz implica que

\[|C(t)| \leq C(0)\]

3. Las funciones de correlación son invariables en el tiempo, es decir, su valor depende únicamente del intervalo de tiempo entre las dos mediciones del observable:

\[\langle A(t) A(0)\rangle=\left\langle A\left(t-t_{0}\right) A\left(t_{0}\right)\right\rangle=\langle A(0) A(-t)\rangle\]

4. La invarianza temporal imparte las siguientes identidades en la derivada de tiempo de una función de correlación de tiempo:

\[\dot{C}(t)=\langle\dot{A}(t) A(0)\rangle=-\langle A(0) \dot{A}(-t)\rangle=-\langle A(t) \dot{A}(0)\rangle\]

5. Si el valor de equilibrio de\(A\) es\(\langle A\rangle_{e q}=0\), entonces el límite de largo plazo de la función de correlación es cero,

\[\lim _{t \rightarrow \infty}\langle A(t) A(0)\rangle=\langle A\rangle_{e q}\langle A(0)\rangle=0\]

6. Para los sistemas cuánticos, las propiedades de invarianza en el tiempo implican eso\(C(-t)=C^{*}(t)\). En el límite clásico, la función de correlación siempre es de valor real, por lo que esta relación se vuelve\(C(-t)=\)\(C(t)\) y\(C(t)\) es así pareja. El hecho de que las funciones de correlación clásicas sean de valor real debería parecer sensato porque podemos (y hacemos) medir funciones de correlación todos los días para sistemas clásicos, por ejemplo, cuando tratamos de regular un cordón colgando del techo. En este caso, determinamos el momento y el lugar adecuados para aplicar una fuerza estable externa buscando correlaciones de tiempo entre los diversos movimientos que experimenta el cordón. Tenga en cuenta que\(C(t)\) es impar con\(C(0)=0\) para las funciones clásicas de correlación de tiempo.
7. Para los sistemas ergódicos, la función de correlación de tiempo se puede calcular como un promedio de tiempo en lugar de un promedio de conjunto:

\[\langle A(t) A(0)\rangle=\lim _{\tau \rightarrow \infty} \frac{1}{\tau} \int_{0}^{\tau} A\left(t+\tau^{\prime}\right) A\left(\tau^{\prime}\right) d \tau^{\prime}\]

Dado que la mayoría de los sistemas susceptibles de análisis por los métodos de la mecánica estadística son inherentemente ergódicos, generalmente somos libres de elegir cualquier formulación con la que sea más fácil trabajar. El promedio de tiempo suele ser más fácil de implementar experimentalmente porque solo requiere integración a lo largo de una trayectoria en lugar de un muestreo simultáneo de cada estado accesible al sistema.

Ejemplo: El oscilador armónico lineal clásico con masa\(m\) y frecuencia\(\omega\) obedece a la ecuación de movimiento

\[\ddot{x}+\omega^{2} x=0\]

Si proporcionamos condiciones iniciales\(x(0)\) y\(\dot{x}(0)=v(0)\), entonces esta ecuación de movimiento tiene la solución de forma cerrada

\[x(t)=x(0) \cos \omega t+\frac{v(0)}{\omega} \sin \omega t\]

Tomando el producto interno de\(x(t)\) con el valor inicial\(x(0)\), encontramos

\[\langle x(t) x(0)\rangle=\left\langle x^{2}(0)\right\rangle \cos \omega t+\frac{\langle v(0) x(0)\rangle}{\omega} \sin \omega t\]

El segundo término es cero porque\(\langle x(0)\rangle=0\), por lo que la función de correlación de tiempo es solo

\[C(t)=\left\langle x^{2}(0)\right\rangle \cos \omega t\]

Finalmente, invocando el resultado de equipartición\(\left\langle x^{2}(0)\right\rangle=\frac{k T}{m \omega^{2}}\), donde\(k\) está la constante de Boltzmann, la función de correlación para el oscilador armónico lineal clásico es

\[C(t)=\frac{k T}{m \omega^{2}} \cos \omega t\]