2.2: Teoría de Regresión Onsager

A primera vista, la relajación de las perturbaciones macroscópicas de no equilibrio en un sistema puede parecer completamente ajena a la regresión de las fluctuaciones microscópicas en el sistema de equilibrio correspondiente. Sin embargo, están íntimamente relacionados por los llamados teoremas de fluctuación-disipación. La existencia de este vínculo entre las fluctuaciones microscópicas y la relajación macroscópica fue conjeturada por Lars Onsager en 1931, unos veinte años antes de que finalmente se demostrara ser cierta; de ahí que a menudo se le refiera como la hipótesis de regresión de Onsager.

Para formular la hipótesis, consideramos un observable\(A\) con\(\langle A\rangle_{e q}=0\) que adquiere un valor promedio de no equilibrio\(\Delta A\) debido a una fuerza externa aplicada\(f\) que actúa durante el intervalo de tiempo\(t \leq 0\) pero que se convierte idénticamente cero para\(t>0\).

Para\(t \leq 0\), el promedio de conjunto de se\(\Delta A\) puede expresar como

\[\Delta A=\frac{\left\langle A e^{-\beta(H-f A)}\right\rangle}{\left\langle e^{-\beta(H-f A)}\right\rangle} \approx \beta f\left[\langle A(0) A(0)\rangle-\langle A(0)\rangle^{2}\right]=\beta f C(0)\]

donde la aproximación que se está haciendo es el truncamiento de la serie Taylor para cada exponencial a primer orden.

Pues\(t>0\), el sistema evoluciona según\(H\) en lugar de\(H-f A\), por lo que ya no\(\Delta A\) es estacionario, sino que adquiere una dependencia del tiempo:

\[\Delta A=\frac{\left\langle A(t) e^{-\beta(H-f A)}\right\rangle}{\left\langle e^{-\beta(H-f A)}\right\rangle} \approx \beta f\left[\langle A(t) A(0)\rangle-\langle A(0)\rangle^{2}\right]=\beta f C(t)\]

La hipótesis de Onsager establece que la relajación del valor de no equilibrio de\(\Delta A\) está relacionada con su valor\(t=0\) en la misma manera que la función de correlación de tiempo para una fluctuación espontánea se relaciona con su valor en\(t=0\):

\[\frac{\Delta A(t)}{\Delta A(0)}=\frac{C(t)}{C(0)}\]

Ejemplo\(\PageIndex{1}\)

La teoría del estado de transición de la cinética química se puede formular a través de la relación Onsager que acabamos de presentar. Considerar un equilibrio químico establecido entre dos especies A y B,

\[\mathrm{A} \underset{k_{b}}{\stackrel{k_{f}}{\rightleftharpoons}} \mathrm{B}\]

con constante de velocidad hacia adelante\(k_{f}\) y constante de tasa hacia atrás\(k_{b}\).

Poblaciones de equilibrio

Podemos describir la dinámica poblacional de A y B determinísticamente en el límite macroscópico a través de un par de ecuaciones diferenciales acopladas,

\[\left\{\begin{array}{l} \dot{P}_{\mathrm{A}}=-k_{f} P_{\mathrm{A}}+k_{b} P_{\mathrm{B}} \\ \dot{P}_{\mathrm{B}}=k_{f} P_{\mathrm{A}}-k_{b} P_{\mathrm{B}} \end{array}\right.\]

El estado de equilibrio de este sistema satisface la condición de equilibrio detallada

\[k_{f}\left\langle P_{\mathrm{A}}\right\rangle=k_{b}\left\langle P_{\mathrm{B}}\right\rangle\]

donde los corchetes angulares denotan los valores de equilibrio de las poblaciones. Tomando las poblaciones para ser normalizadas a la unidad\(\left\langle P_{\mathrm{A}}\right\rangle+\left\langle P_{\mathrm{B}}\right\rangle=1\),, podemos expresar\(\left\langle P_{\mathrm{A}}\right\rangle\) en términos de las constantes de tasa:

\[\left\langle P_{\mathrm{A}}\right\rangle=\frac{\left\langle P_{\mathrm{A}}\right\rangle}{\left\langle P_{\mathrm{A}}\right\rangle+\left\langle P_{\mathrm{B}}\right\rangle}=\frac{k_{b}}{k_{f}+k_{b}}\]

Por simplicidad notacional, introducimos\(k=k_{f}+k_{b}\) y nos referimos a las poblaciones de equilibrio\(\left\langle P_{\mathrm{A}}\right\rangle\) y\(\left\langle P_{\mathrm{B}}\right\rangle\) por\(q_{\mathrm{A}}\) y\(q_{\mathrm{B}}\), respectivamente. Con esta nueva notación, podemos expresar las poblaciones de equilibrio de A y B como

\[\left\{\begin{array}{l} q_{\mathrm{A}}=\frac{k_{b}}{k} \\ q_{\mathrm{B}}=\frac{k_{f}}{k} \end{array}\right.\]

Si el estado inicial es toda la especie A, la solución a las ecuaciones diferenciales acopladas indica una decaimiento al equilibrio con constante de velocidad\(k\), que podemos escribir en términos de\(\Delta P_{\mathrm{A}}(t)=P_{\mathrm{A}}(t)-q_{\mathrm{A}}\) como

\[\Delta P_{\mathrm{A}}(t)=\Delta P_{\mathrm{A}}(0) e^{-k t}\]

Dejando de lado este resultado por un momento, tenga en cuenta que si consideramos que las energías de las especies A y B son pozos potenciales conectados a lo largo de una coordenada de reacción\(x\), entonces podemos escribir una expresión para la fluctuación en el número de ocupación\(n\) para cada especie como una función de\(x\). La barrera entre los pozos de potencial A y B es máxima en\(x=x_{b}\); ver Figura 2.2.

Figura 2.2: Proyección de la superficie de energía potencial conectando las especies A y B a lo largo de la coordenada\(x\)

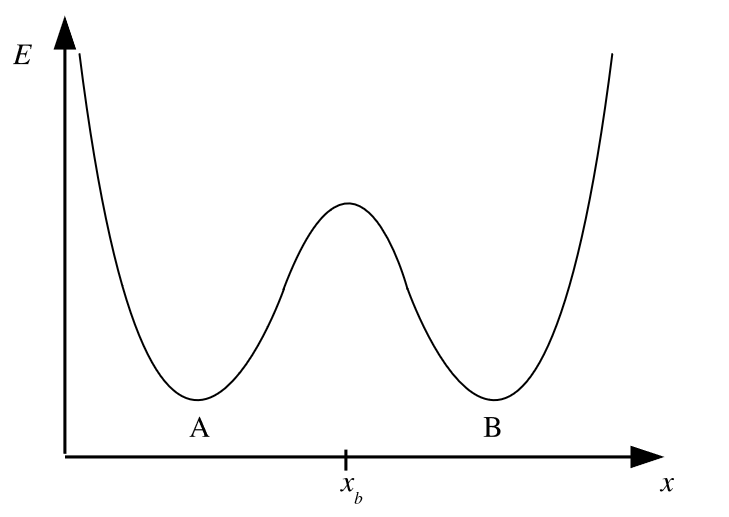
Aplicación de la hipótesis de regresión Onsager

Para reflejar el hecho de que una partícula a la izquierda de la barrera es la especie A y una partícula a la derecha es la especie B, escribimos los números de ocupación en términos de la función de paso Heaviside,

\[\left\{\begin{array}{l} n_{\mathrm{A}}=\theta\left(x_{b}-x\right) \\ n_{\mathrm{B}}=\theta\left(x-x_{b}\right) \end{array}\right.\]

donde\(\left\langle n_{\mathrm{A}}\right\rangle=q_{\mathrm{A}}\) y\(\left\langle n_{\mathrm{B}}\right\rangle=q_{\mathrm{B}} .\) Aplicando la hipótesis de regresión de Onsager a este ejemplo, podemos relacionar la disipación de\(P_{\mathrm{A}}\) con las fluctuaciones en el número de ocupación de la siguiente manera:

\[\frac{C(t)}{C(0)}=\frac{\left\langle\delta n_{\mathrm{A}}(t) \delta n_{\mathrm{A}}(0)\right\rangle}{\left\langle\delta n_{\mathrm{A}}^{2}(0)\right\rangle}=\frac{\Delta P_{\mathrm{A}}(t)}{\Delta P_{\mathrm{A}}(0)}=e^{-k t}\]

La segunda igualdad surge de nuestra ecuación de tasa integrada para la disipación de\(P_{\mathrm{A}}\). También tenga en cuenta que

\[\left\langle\delta n_{\mathrm{A}}^{2}\right\rangle=\left\langle n_{\mathrm{A}}^{2}\right\rangle-\left\langle n_{\mathrm{A}}\right\rangle^{2}=q_{\mathrm{A}}-q_{\mathrm{A}}^{2}=q_{\mathrm{A}}-q_{\mathrm{A}}\left(1-q_{\mathrm{B}}\right)=q_{\mathrm{A}} q_{\mathrm{B}}\]

Diferenciando la relación fluctuación-disipación anterior con respecto a\(t\) e invocando la identidad que se acaba de mostrar, encontramos

\[k e^{-k t}=-\frac{\left\langle\delta \dot{n}_{\mathrm{A}}(t) \delta n_{\mathrm{A}}(0)\right\rangle}{\left\langle\delta n_{\mathrm{A}}^{2}(0)\right\rangle}=\frac{\left\langle n_{\mathrm{A}}(t) \dot{n}_{\mathrm{A}}(0)\right\rangle}{q_{\mathrm{A}} q_{\mathrm{B}}}\]

Refundiendo esta ecuación en términos de la coordenada de reacción\(x\), se llega a una expresión para la dependencia del tiempo de la constante de velocidad hacia adelante\(k_{f}(t)\),

\[k_{f}(t)=k_{f} e^{-k t}=\frac{\left\langle\theta\left(x(t)-x_{b}\right) \delta\left(x_{b}-x(0)\right) v\right\rangle}{\left\langle\theta\left(x_{b}-x(t)\right)\right\rangle}\]

donde\(v=\dot{n}_{\mathrm{A}}(0)\) es la velocidad inicial de reacción.

Expresión para la constante de velocidad TST

Finalmente, para determinar la constante de velocidad de la teoría del estado de transición (TST), consideramos nuestra expresión dependiente del tiempo\(k_{f}\) en el límite de tiempo corto, ya que los estados de transición generalmente solo sobreviven unas pocas vibraciones moleculares. En este límite,

\[\lim _{t \rightarrow 0^{+}} k_{f}(t)=\frac{\left\langle\theta\left(x\left(0^{+}\right)-x_{b}\right) \delta\left(x_{b}-x(0)\right) v\right\rangle}{\left\langle n_{\mathrm{A}}\right\rangle}=\frac{\left\langle\theta(v) \delta\left(x_{b}-x(0)\right) v\right\rangle}{\left\langle n_{\mathrm{A}}\right\rangle}\]

A partir de la teoría cinética de los gases, reconocemos que

\[\langle\theta(v) v\rangle=\sqrt{\frac{k_{B} T}{2 \pi m}}=(2 \pi m \beta)^{-1 / 2}\]

Si estipulamos ahora que la altura de la barrera es\(E_{b}\), algún reordenamiento de las fórmulas precedentes revela que

\[\frac{\left\langle\delta\left(x_{b}-x\right)\right\rangle}{\left\langle\theta\left(x_{b}-x\right)\right\rangle}=\sqrt{\frac{m \omega^{2} \beta}{2 \pi}} e^{-\beta E_{b}}\]

donde\(\omega\) está la frecuencia fundamental del pozo potencial izquierdo. De ello se deduce que la constante de velocidad TST toma la forma simple

\[k_{T S T}=\frac{\omega}{2 \pi} e^{-\beta E_{b}}\]

Para concluir nuestra excursión a la cinética de TST, tenga en cuenta que la relación

\[\frac{k(t)}{k_{T S T}}=\frac{\left\langle\theta\left(x(t)-x_{b}\right) \delta\left(x(0)-x_{b}\right) v\right\rangle}{\left\langle\theta\left(x\left(0^{+}\right)-x_{b}\right) \delta\left(x(0)-x_{b}\right) v\right\rangle}\]

siempre es menor o igual a uno. Este resultado indica que el flujo TST está parcialmente atrapado en el pozo de producto mientras que parte del flujo TST vuelve a roscarse al estado reactivo. Este resultado está en consonancia con nuestra intuición de la dinámica química en que cada reacción macroscópica es, hasta cierto punto, un proceso de establecer el equilibrio más que un flujo perfecto de todos los reactivos a todos los productos.