3.1: Dispersión de luz

Funciones de dispersión y correlación

Una partícula o campo de luz que se propaga a través del espacio puede ser descrito por un vector de onda\(\vec{k}\). La dirección de\(k\) indica la dirección de propagación de la onda, y la magnitud de\(k\) indica el número de onda, o longitud de onda inversa, de la onda. La dispersión ocurre cuando una onda de propagación se encuentra con un medio que altera la magnitud o dirección de su vector de onda. En esta sección, mostraremos que el comportamiento de la luz dispersada desde un medio está relacionado con las funciones de correlación de densidad del medio. Como resultado, se pueden usar experimentos de dispersión de luz para sondear la estructura de un material.

Dispersión elástica

Neutrón o dispersión de luz

En esta sección, queremos describir el comportamiento de una partícula o campo de luz que sufre dispersión elástica desde un medio. Esta discusión podría aplicarse a la dispersión de rayos X, protones, neutrones o electrones, entre otros.

La dispersión elástica ocurre cuando no hay transferencia de energía de la partícula al medio de dispersión. La dirección del vector de onda de la partícula cambia, pero su número de onda (o frecuencia) sigue siendo el mismo. En la Figura 3.1 se representa un esquema del proceso de dispersión. La partícula incidente o campo de luz con vector de onda\(\overrightarrow{k_{o}}\) se dispersa de la muestra en el punto\(\vec{r}\), cambiando su vector de onda a\(\overrightarrow{k_{f}}\). El vector\(\overrightarrow{k_{f}}\) tiene la misma magnitud que\(\overrightarrow{k_{o}}\), pero una dirección diferente. La luz dispersada se detecta en el punto\(\overrightarrow{r^{\prime}}\).

Figura 3.1: Dispersión elástica de una partícula o campo de luz de un medio

La partícula dispersa o el campo de luz se pueden modelar como una onda esférica. La expresión mecánica cuántica para esta onda es

\[\Psi_{s}=\frac{i}{\hbar} \int \frac{e^{i k\left|\vec{r}-\overrightarrow{r^{\prime}}\right|}}{\left|\vec{r}-\overrightarrow{r^{\prime}}\right|} e^{i \overrightarrow{k_{o}} \cdot \overrightarrow{r^{\prime}}} \rho\left(\overrightarrow{r^{\prime}}\right) d \overrightarrow{r^{\prime}}\]

donde\(\rho(\vec{r})\) está la densidad de los agentes de dispersión y la integral se lleva a cabo sobre todos los agentes de dispersión.

En la mayoría de los experimentos de dispersión de luz, la distancia desde la muestra hasta el detector de luz es significativamente mayor que el tamaño de la muestra misma. En este caso es válido hacer el supuesto de que\(r>>r^{\prime}\). Entonces

\[e^{i k\left|\vec{r}-\vec{r}^{\prime}\right|} \rightarrow e^{i k r-i \overrightarrow{k_{f}} \cdot \overrightarrow{r^{\prime}}}\]

y la función wavefunction se puede escribir

\[\Psi_{s}=\frac{i}{\hbar} \frac{e^{i k r}}{r} \int \rho\left(\overrightarrow{r^{\prime}}\right) e^{-i\left(\overrightarrow{k_{f}}-\overrightarrow{k_{o}}\right) \cdot \overrightarrow{r^{\prime}}} d \overrightarrow{r^{\prime}}=\frac{i}{\hbar} \frac{e^{i k r}}{r} \int \rho\left(\overrightarrow{r^{\prime}}\right) e^{-i \vec{k} \cdot \vec{r}^{\prime}} d \overrightarrow{r^{\prime}}\]

donde\(\vec{k}=\overrightarrow{k_{f}}-\overrightarrow{k_{o}}\) está la diferencia entre el vector de onda inicial y disperso.

También podemos suponer que el medio está compuesto por partículas puntuales, por lo que la densidad es la suma sobre todos los puntos

\[\rho(\vec{r})=\sum_{i=1}^{N} a_{i} \delta\left(\vec{r}-\vec{r}_{i}\right)=a \sum_{i=1}^{N} \delta\left(\vec{r}-\vec{r}_{i}\right)\]

Entonces la función de onda simplifica a

\[\Psi_{s}=\frac{i}{\hbar} \frac{e^{i k r}}{r} a \sum_{i=1}^{N} e^{-i \vec{k} \cdot \overrightarrow{r_{i}}} \propto a \sum_{i=1}^{N} e^{-i \vec{k} \cdot \overrightarrow{r_{i}}}\]

En experimentos de dispersión de luz, la cantidad medida es la intensidad de la luz dispersada sobre el ángulo abarcado por el detector. Esta cantidad se llama sección transversal de dispersión\(\frac{d \sigma}{d \Omega}\), y es proporcional al cuadrado de la función de onda:

\[I(\vec{k})=\left|\Psi_{s}\right|^{2} \propto \frac{1}{r^{2}} \frac{d \sigma}{d \Omega}=\frac{a^{2}}{r^{2}}\left\langle\left.\sum_{i=1}^{N} e^{-i \vec{k} \cdot \vec{r}_{i}}\right|^{2}\right\rangle=\frac{a^{2}}{r^{2}} N S(\vec{k})\]

donde\(S(\vec{k})\) se llama el factor de estructura estática, y se define como:

\[S(\vec{k})=\frac{1}{N}\left\langle\left|\sum_{i=1}^{N} e^{-i \vec{k} \cdot \vec{r}_{i}}\right|^{2}\right\rangle\]

Para encontrar la intensidad de dispersión, debemos evaluar este término.

El factor de estructura estática

El factor de estructura estática se puede reescribir como:

\[S(k)=\frac{1}{N}\left\langle\rho_{k} \rho_{-k}\right\rangle\]

donde

\[\rho_{k}=\int e^{-i \vec{k} \cdot \vec{r}} \rho(\vec{r}) d \vec{r}\]

y\(\rho(r)\) es la densidad de números locales. Para un líquido homogéneo,\(\langle\rho(r)\rangle=\rho_{o}\).

Para modelar sistemas reales, podemos simplificar los cálculos expresando las correlaciones de densidad como una suma de la densidad homogénea\(\rho_{o}\) y las fluctuaciones locales\(\delta \rho\).

\[\rho(r)=\rho_{o}+\delta \rho\]

Usando esta separación, la función de dispersión se puede escribir en dos piezas:

\[S(k)=\frac{1}{N}\left\langle\rho_{k} \rho_{-k}\right\rangle=\rho_{0}(2 \pi)^{3} \delta(\vec{k})+\frac{1}{N}\left\langle\delta \rho_{k} \delta \rho_{-k} \mid\right\rangle\]

El primer término surge del fondo homogéneo y se denomina dispersión hacia adelante. El segundo término da la dispersión de las fluctuaciones de densidad. En un gas ideal, no hay interacción entre las partículas\(\delta \rho=0\), por lo que solo hay dispersión hacia adelante.

La función de correlación de densidad También es útil pensar en la dispersión en el espacio real. Definir la función de correlación de densidad\(G(\vec{r})\) como la transformada de Fourier\(S(k)\) en el espacio de coordenadas.

\[\begin{aligned} G(\vec{r})=\frac{1}{(2 \pi)^{3}} \int S(\vec{k}) e^{-i \vec{k} \cdot \vec{r}} d \vec{k} \\ =\frac{1}{N} \frac{1}{(2 \pi)^{3}} \int e^{-i \vec{k} \cdot \vec{r}}\left\langle\sum_{i} e^{i \vec{k} \cdot \vec{r}_{i}} \sum_{j} e^{-i \vec{k} \cdot \vec{r}_{j}}\right\rangle d \vec{k} \\ =\frac{1}{N} \sum_{i, j}\left\langle\delta\left(\vec{r}-\vec{r}_{i, j}\right)\right\rangle \end{aligned}\]

A partir de esto, podemos ver que la transformada de Fourier del factor de estructura da probabilidad de encontrar dos partículas separadas por un vector\(\vec{r}\).

También podemos escribir la función de correlación de densidad en una forma ligeramente diferente:

\[\begin{aligned} G(\vec{r})=\frac{1}{N} \sum_{i, j} \int d \overrightarrow{r_{o}}\left\langle\delta\left(\overrightarrow{r_{i}}-\overrightarrow{r_{o}}-\vec{r}\right) \delta\left(\overrightarrow{r_{j}}-\overrightarrow{r_{o}}\right)\right\rangle \\ =\frac{1}{N} \int d \overrightarrow{r_{o}}\left\langle\rho\left(\overrightarrow{r_{o}}+\vec{r}\right) \rho\left(\overrightarrow{r_{o}}\right)\right\rangle=\frac{V}{N}\langle\rho(\vec{r}) \rho(0)\rangle=\frac{1}{\rho_{o}}\langle\rho(\vec{r}) \rho(0)\rangle \end{aligned}\]

La función de distribución de pares\(\quad\)

Para comprender mejor la interpretación física del factor de estructura y la función de correlación de densidad, podemos reescribirlos en términos de la función de distribución de pares\(g(r)\). La función de distribución de pares viene dada por:

\[g(r)=\frac{1}{N^{2}} \sum_{i \neq j}\left\langle\delta\left(\vec{r}-\vec{r}_{i, j}\right)\right\rangle\]

Esto da la probabilidad de que, si tengo una sola partícula\(i\), podré encontrar otra partícula\(j\) a una\(\vec{r}\) distancia. Se define sólo para términos con\(i \neq j\). Podemos escribir\(g(r)\) como:

\[g(r)=h(r)+1\]

donde\(h(r)\) está la función de correlación de pares. La transformada de Fourier de la función de distribución de pares se puede escribir:

\[\tilde{g}(\vec{k})=\tilde{h}(\vec{k})+(2 \pi)^{3} \delta(\vec{k})\]

Esto nos permite reescribir el factor de estructura y la función de correlación de densidad en términos de las interacciones entre pares individuales de partículas.

Figura 3.2: La función de distribución de pares

Para escribir el factor de estructura\(S(k)\) y la función de correlación de densidad\(G(r)\) en términos de la función de distribución de pares, separe las sumaciones en términos con\(i=j\) y términos con\(i \neq j\). El factor de estructura está escrito:

\[S(k)=\frac{1}{N} \sum_{i, j}\left\langle e^{-i k r_{i}} e^{i k r_{j}}\right\rangle\]

Los términos con\(i=j\) cada uno aportan un valor de\(\frac{1}{N}\). Después de tomar la suma sobre todas\(N\) las partículas, esto da un valor de 1.

\[S(k)=1+\sum_{i \neq j}\left\langle e^{-i k\left(r_{i}-r_{j}\right)}\right\rangle=1+\rho \tilde{g}(k)=1+\rho \tilde{h}(\vec{k})+(2 \pi)^{3} \delta(\vec{k}) \rho\]

Ahora bien, los dos primeros términos\(1+\rho \tilde{h}(\vec{k})\) dan la dispersión debido a la estructura molecular, o fluctuaciones. El tercer término da la dispersión hacia adelante, que como comentamos anteriormente es la dispersión que esperaríamos en un sistema sin fluctuaciones (un gas ideal).

La función de correlación de densidad está escrita:

\[G(\vec{r})=\frac{1}{N}\left\langle\sum_{i, j} \delta\left(r_{i, j}-r\right)\right\rangle\]

cuando\(i=j\), estamos discutiendo una sola partícula. Por lo tanto,\(r_{i, j}=0\) y cada término contribuye\(\frac{1}{N} \delta(\vec{r})\). Después de tomar la suma sobre todas\(N\) las partículas, las\(N\) cancelas y nos quedamos con\(\delta(\vec{r})\).

\[\begin{aligned} & G(\vec{r})=\delta(\vec{r})+\frac{1}{N}\left\langle\sum_{i \neq j} \delta\left(r_{i, j}-r\right)\right\rangle \\ =& \delta(\vec{r})+\rho g(\vec{r})=\delta(\vec{r})+\rho(h(\vec{r})+1) \end{aligned}\]

Al escribir las expresiones para\(S(\vec{k})\) y\(G(\vec{r})\) en términos de\(g(\vec{r})\), su interpretación física se vuelve más clara. La función de distribución de pares para un líquido típico y un sólido típico se muestran en la Figura\(3.3\) y la Figura\(3.4\). Si una partícula tiene un radio\(d\), entonces claramente ninguna otra partícula puede estar más cerca que la distancia\(d\). Por lo tanto, tanto para el sólido como para el líquido,\(g(\vec{r})\) tiene un valor de 0 desde una distancia 0 a una distancia\(d\). En este punto, la probabilidad aumenta rápidamente y comienza a oscilar alrededor de un valor de 1. En un líquido, hay una estructura de corto alcance ya que las interacciones intermoleculares débiles forman una serie de conchas de solvatación alrededor de una partícula. Sin embargo, estas fuerzas solo actúan a corto alcance, y a medida que la distancia aumenta la correlación disminuye a cero. En un sólido, la estructura persiste a lo largo de la muestra, y por lo tanto las oscilaciones no se decaen.

Dispersión inelástica

En la sección anterior se describió el comportamiento de una partícula al sufrir un evento de dispersión elástica. En esta sección, abordaremos el fenómeno de la dispersión inelástica, que se aplica principalmente a los campos de luz. La dispersión inelástica ocurre cuando la luz dispersa transfiere algo de energía al material de dispersión. Mientras que un evento de dispersión elástica solo causa un cambio en la dirección del vector de onda, un evento de dispersión inelástica provoca tanto un cambio en la dirección como en el número de onda de la luz dispersada. En otras palabras, la onda dispersa se convierte en frecuencia dispersa. La\(3.5\) figura muestra un esquema de un evento de dispersión inelástica.

Intensidad dispersa

Para calcular la intensidad de la luz dispersada a partir de un evento de dispersión inelástica, podemos seguir un proceso muy similar al que usamos para la dispersión elástica: modelar la luz dispersada como una onda esférica, y simplificarla asumiendo que la distancia desde la muestra hasta el detector de luz es grande comparada con el tamaño de la muestra, y que el medio esté compuesto por partículas puntuales. Sin embargo, hay una diferencia importante. Dado que la luz dispersada puede transferir energía al material, la posición de las partículas ahora depende del tiempo. La función de onda dispersa es entonces:

Figura 3.3: Función de distribución de pares para un líquido

Figura 3.4: Función de distribución de pares para un sólido

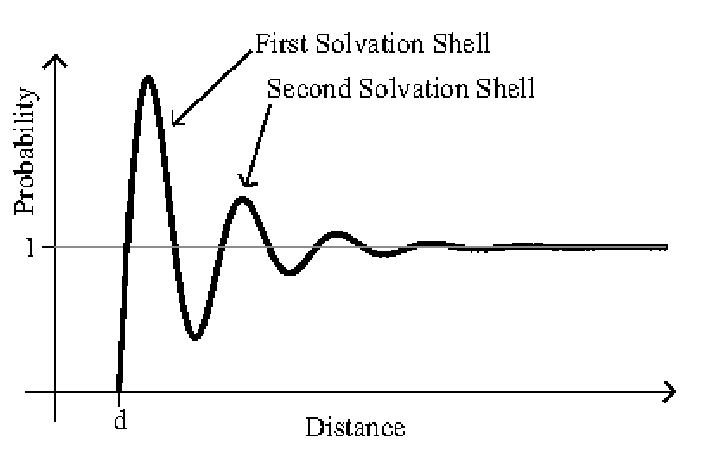
Figura 3.5: Esquema de un Evento de Dispersión Inelástica

\[\Psi_{s} \propto \frac{a}{r} \sum_{i=1}^{N} e^{-i \vec{k} \cdot \vec{r}_{i}(t)}\]

que da una sección transversal diferencial de:

\[\frac{d \sigma}{d \Omega d \omega}=a^{2}\left\langle\sum_{i} e^{-i \vec{k} \cdot \overrightarrow{r_{i}}(t)} \sum_{j} e^{-i \vec{k} \cdot \overrightarrow{r_{j}}(t)}\right\rangle\]

Al tomar la transformada temporal de Fourier, podemos encontrar el factor de estructura:

\[\begin{aligned} \frac{d \sigma}{d \Omega d \omega}=a^{2} \int e^{i w t} &\left\langle\sum_{i} e^{-i \vec{k} \cdot \vec{r}_{i}(t)} \sum_{j} e^{-i \vec{k} \cdot \vec{r}_{j}(t)} d t\right\rangle \\ &=a^{2} N S(\vec{k}, \omega) \end{aligned}\]

Tenga en cuenta que el factor\(S\) de estructura ahora depende tanto del vector de onda como\(\vec{k}\) de la frecuencia\(\omega\). Por lo tanto, se llama el Factor de Estructura Dinámica.

La función de dispersión intermedia

La función de dispersión intermedia se define como la transformada de Fourier del factor de estructura dinámica en tiempo real.

\[\begin{aligned} F(\vec{k}, t)=\frac{1}{2 \pi} \int S(\vec{k}, \omega) e^{i \omega t} d \omega \\ S(\vec{k}, \omega)=\int F(\vec{k}, t) e^{-i \omega t} d t \end{aligned}\]

Se llama la función de dispersión intermedia es porque tiene una variable, la dimensión espacial\(k\), expresada en el espacio de Fourier, y la otra variable, la dimensión de tiempo\(t\), expresada en el espacio real. Se puede expresar explícitamente como:

\[F(\vec{k}, t)=\frac{1}{N}\left\langle\rho_{k}(t) \rho_{-k}(0)\right\rangle\]

donde:

\[\rho_{k}(t)=\sum_{i} e^{-i \vec{k} \cdot \overrightarrow{r_{i}}(t)}\]

Tenga en cuenta que esta función se ve idéntica al factor estructural estático de la sección 1, excepto que ahora la densidad es una función del tiempo.

La función Van Hove

La función Van Hove se define como la transformada de Fourier de la función de dispersión intermedia en el espacio real.

\[G(\vec{r}, t)=\frac{1}{(2 \pi)^{3}} \int F(\vec{k}, t) e^{i \vec{k} \cdot \vec{r}} d \vec{k}=\frac{1}{N} \sum_{i, j}\left\langle\delta\left(\vec{r}_{i}(t)-\overrightarrow{r_{j}}(0)-\vec{r}\right)\right\rangle\]

La función Van Hove también se puede expresar como

\[\begin{aligned} G(\vec{r}, t)=\frac{1}{N} \int d \overrightarrow{r_{o}}\left\langle\sum_{i} \delta\left(\overrightarrow{r_{i}}(t)-\vec{r}-\overrightarrow{r_{o}}\right) \sum_{j} \delta\left(\overrightarrow{r_{j}}(0)-\overrightarrow{r_{o}}\right)\right\rangle \\ =\frac{1}{N} \int d \overrightarrow{r_{o}}\left\langle\rho\left(\vec{r}+\overrightarrow{r_{o}}, t\right) \rho\left(\overrightarrow{r_{o}}, 0\right)\right\rangle \\ =\frac{V}{N}\langle\rho(\vec{r}, t) \rho(0,0)\rangle \end{aligned}\]

donde\(\frac{V}{N}=\rho_{o}^{-1}\). La función Van Hove describe la fluctuación de densidades en diferentes momentos y posiciones.

Puede ser difícil hacer un seguimiento de las muchas funciones utilizadas para describir la dispersión inelástica. En la siguiente tabla se resumen estas funciones y sus diferentes variables espaciales y temporales.

Nombre	Símbolo	Dimensión espacial	Dimensión Temporal
Factor de estructura dinámica	\(S(\vec{k}, \omega)\)	Fourier,\(\vec{k}\)	Fourier,\(\omega\)
Función de dispersión intermedia	\(F(\vec{k}, t)\)	Fourier,\(\vec{k}\)	Real,\(t\)
Función Van Hove	\(G(\vec{r}, t)\)	Real,\(\vec{r}\)	Real,\(t\)

5. Si solo nos interesa la estructura espacial, podemos realizar una suma sobre la dimensión temporal:

\[S(\vec{k})=\frac{1}{2 \pi} \int S(\vec{k}, \omega) d \omega=F(\vec{k}, 0)\]

Esto da la estructura espacial.

6. La densidad se puede expresar nuevamente como la suma de un fondo constante\(\rho_{o}\) y fluctuaciones\(\delta \rho:\)

\[\rho=\rho_{o}+\delta \rho\]

Entonces el factor de estructura dinámica se puede expresar como

\[S(\vec{k}, w)=(2 \pi)^{4} \delta(\vec{k}) \delta(\omega) \rho_{o}+\int e^{i \omega t} \frac{1}{N}\left\langle\delta \rho_{k}(t) \delta \rho_{-k}(0)\right\rangle d t\]

En el primer término,\(\vec{k}=0\) y\(\omega=0\). Esta es la onda delantera, elástica, no dispersa para un gas ideal. El segundo término da el espectro de fluctuaciones de densidad en el fluido.