3.2: Ecuaciones hidrodinámicas de Navier-Stokes
- Page ID
- 76110
Ecuaciones Básicas
Conservación de la Masa
Considere un volumen fijo en el espacio, como el que se muestra en la Figura\(3.6\)
El número total de partículas en la región en cualquier momento se puede encontrar tomando la suma sobre la densidad en todos los puntos:
\[N=\int_{V} \rho(\vec{r}) d \vec{r}\]
El cambio en el\(N\) tiempo depende del flujo, que se puede encontrar por integración sobre una superficie o un volumen
\[\frac{d N}{d t}=J_{i n}-J_{o u t}=-\oint_{\partial V} \vec{J} \cdot d \vec{S}=-\int \vec{\nabla} \cdot \vec{J} d V\]
Podemos reescribir el cambio en el número de partículas en términos de densidad:
\[\frac{d N}{d t}=\int \frac{d \rho}{d t} d \vec{r}=-\int \vec{\nabla} \cdot \vec{J} d V\]
Eliminar la integración espacial y reorganizar
\[\frac{d \rho}{d t}+\vec{\nabla} \cdot \vec{J}=0\]
Para expresar la ecuación en términos de densidad y velocidad, reescribimos el flujo como\(\vec{J}=\rho \vec{v}\), de manera que
\[\nabla \vec{J}=\vec{\nabla} \cdot(\rho \vec{v})\]
Entonces la conservación de la masa viene dada por:
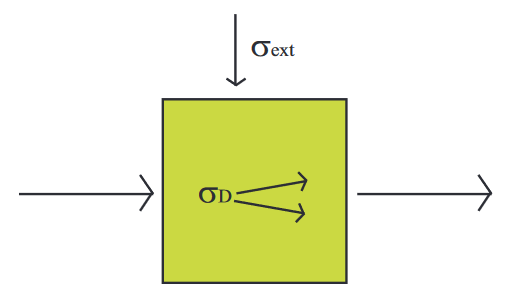
Ecuaciones de continuidad En general, para cualquier cantidad dinámica\(A\), podemos definir una densidad\(\rho\) y escribir una ecuación de continuidad.
Esta ecuación estará determinada por la interacción entre corrientes\(\vec{J}\) y fuentes\(\sigma\).
\[\frac{\partial \rho A}{\partial t}+\vec{\nabla} \cdot \vec{J}=\sigma\]
La corriente total\(\vec{J}\) puede modelarse como la suma de un término conservador\(\vec{J}_{V}=\rho A \vec{v}\) y un término disipativo\(\vec{J}_{D}\).
\[\vec{J}=\vec{J}_{V}+\vec{J}_{D}\]
La fuente\(\sigma\) puede escribirse como la suma de fuentes externas\(\sigma_{\text {ext }}\) y fuentes de producción\(\sigma_{D}\)
\[\sigma=\sigma_{\text {ext }}+\sigma_{D}\]
Por lo tanto, la ecuación de continuidad para\(A\) puede escribirse de manera más explícita como
\[\frac{\partial \rho A}{\partial t}+\vec{\nabla} \cdot(\rho A \vec{v})+\vec{\nabla} \cdot \vec{J}_{D}=\sigma_{e x t}+\sigma_{D}\]
En el mundo físico hay cinco cantidades conservadas: la densidad, el impulso (en tres direcciones) y la energía (o entropía).
\[A=\{1, m \vec{v}, S\}\]
Por lo tanto, encontraremos cinco ecuaciones de continuidad. Ya encontramos la ecuación de continuidad para la densidad, y en las dos secciones siguientes encontraremos las ecuaciones para el impulso y la entropía.
Ecuación de impulso (ecuaciones de Navier-Stokes)
Para encontrar la ecuación de continuidad para el impulso, sustituya\(A=m \vec{v}\) en la ecuación de continuidad general.
\[\frac{\partial \rho m \vec{v}}{\partial t}+\vec{\nabla} \cdot(\rho m \vec{v}: \vec{v})+\vec{\nabla} \cdot \overrightarrow{\vec{J}}_{D}=\vec{\sigma}_{e x t}+\vec{\sigma}_{D}\]
Suponemos que la fuerza de producción es cero. La fuerza externa es la presión, que actúa para crear un impulso neto o aceleración.
\[\vec{\sigma}_{\text {ext }}=\rho \vec{F}-\vec{\nabla} P\]
Los términos que representan la corriente conservadora y disipativa son ambos tensores. Esto se debe a que el impulso es un vector, y así la corriente, que representa el cambio de impulso, debe ser un tensor. La corriente conservadora viene dada por
\[\overrightarrow{\vec{J}}_{V}=(\rho m \vec{v}: \vec{v})\]
La corriente disipativa es el tensor de tensión\(\overrightarrow{\vec{J}}_{D}=-\overrightarrow{\vec{\Pi}}\). La ecuación de continuidad para el impulso se puede escribir como
\[m \frac{\partial \rho \vec{v}}{\partial t}+\vec{\nabla} \cdot(\rho m \vec{v}: \vec{v})+\vec{\nabla} P=\rho \vec{F}+\vec{\nabla} \cdot \overrightarrow{\vec{\Pi}}\]
Echemos un vistazo más de cerca al tensor de estrés. Para un medio isotrópico, el tensor de tensión se puede expresar como
\[\Pi_{i, j}=\eta_{B}(\vec{\nabla} \cdot \vec{v}) \delta_{i, j}+\eta\left(\partial_{i} v_{j}+\partial_{j} v_{i}-\frac{2}{3}(\vec{\nabla} \cdot \vec{v}) \delta_{i, j}\right)\]
donde\(\eta_{B}\) esta la viscosidad aparente. Da el cambio esperado en el volumen resultante de una tensión aplicada. Así mismo,\(\eta\) es la viscosidad de cizallamiento. Esto da la cantidad esperada de cizallamiento, o cambio de forma, resultante de una tensión aplicada. El término final\(\partial_{i} v_{j}+\partial_{j} v_{i}-\frac{2}{3} \nabla \vec{v} \delta_{i, j}\) es un componente simétrico sin trazas que cambia la forma, pero no el volumen, del medio.
Podemos expresar el cambio en el tensor de estrés como
\[(\vec{\nabla} \cdot \overrightarrow{\mathrm{\Pi}})_{i}=\sum_{j} \nabla_{j} \Pi_{j, i}=\left(\frac{1}{3} \eta+\eta_{B}\right) \nabla_{i}(\vec{\nabla} \cdot \vec{v})+\eta \nabla^{2} v_{i}\]
Con esto, podemos reescribir la ecuación de continuidad de impulso como
\[m \frac{\partial \rho \vec{v}}{\partial t}+\vec{\nabla} \cdot(\rho m \vec{v}: \vec{v})+\vec{\nabla} P=\left(\frac{1}{3} \eta+\eta_{B}\right) \vec{\nabla}(\vec{\nabla} \cdot \vec{v})+\eta \nabla^{2} \vec{v}\]
A esto también se le llama la ecuación de Navier-Stokes.
Ecuación de entropía (difusión de calor)
Para encontrar la ecuación de continuidad para la entropía, sustituya\(A=s\) a la ecuación de continuidad general. En este caso, estamos pensando en la entropía para cada partícula y no en todo el sistema, por lo que\(s\) se usa una minúscula.
\[\frac{\partial \rho s}{\partial t}+\vec{\nabla} \cdot(\rho s \vec{v})+\vec{\nabla} \cdot \vec{J}_{D}=\sigma_{e x t}+\sigma_{D}\]
Podemos simplificar esta expresión asumiendo que no hay fuerzas que creen o destruyan la entropía, por lo que también\(\sigma_{\text {ext }}+\sigma_{D}=0\) sabemos que la entropía fluye de altas temperaturas a bajas temperaturas, por lo que
\[\vec{J}_{D} \propto-\vec{\nabla} \cdot \vec{T}\]
Escribe esto explícitamente usando la constante\(\lambda\)
\[\vec{J}_{D}=-\frac{\lambda \vec{\nabla} T}{T}\]
Luego, sustituya esto para obtener la ecuación de continuidad
\[\frac{\partial \rho s}{\partial t}+\vec{\nabla} \cdot(\rho s \vec{v})-\lambda \vec{\nabla} \cdot\left(\frac{\vec{\nabla} T}{T}\right)=0\]
Ahora tenemos expresiones para las 5 ecuaciones de continuidad para el número de partículas, el impulso y la energía.
\[\begin{aligned} \frac{d \rho}{d t}+\vec{\nabla} \cdot(\rho \vec{v}) &=0 \\ m \frac{\partial \rho \vec{v}}{\partial t}+\vec{\nabla} \cdot(\rho m \vec{v}: \vec{v})+\vec{\nabla} P &=\vec{\nabla} \cdot \overrightarrow{\vec{\Pi}} \\ \frac{\partial \rho s}{\partial t}+\vec{\nabla} \cdot(\rho s \vec{v})-\lambda \vec{\nabla} \cdot\left(\frac{\vec{\nabla} T}{T}\right) &=0 \end{aligned}\]
La solución a este conjunto de ecuaciones da\(\rho(k, t)\). Aunque es imposible de resolver analíticamente, se pueden obtener soluciones aproximadas linealizando las ecuaciones.
Ecuaciones hidrodinámicas linealizadas
Las ecuaciones hidrodinámicas son imposibles de resolver analíticamente. Sin embargo, es posible obtener soluciones aproximadas linealizando las ecuaciones. Definir el operador
\[\mathcal{L}(A)=\frac{\partial A}{\partial t}\]
Para una cantidad independiente del tiempo\(A_{S}\),
\[\mathcal{L}\left(A_{S}\right)=\frac{\partial A_{S}}{\partial t}=0\]
Podemos construir cualquier cantidad\(A\) como la suma de una parte independiente del tiempo, “estable”\(A_{S}\) y una parte fluctuante\(\delta A\)
\[A=A_{S}+\delta A\]
Entonces podemos escribir\(\mathcal{L}(A)\) como una expansión. Si truncamos la expansión en el primer orden, término lineal, encontramos que
\[\mathcal{L}(A)=\mathcal{L}\left(A_{S}+\delta A\right)=\mathcal{L}\left(A_{S}\right)+\mathcal{L}(\delta A)=\frac{\partial \delta A}{\partial t}\]
Para una solución homogénea,\(\rho\) es una constante. No hay movimiento cinético colectivo, solo pequeños movimientos de Boltzmann que promedian a cero. Por lo tanto,\(\overrightarrow{v_{o}}=0\). La entropía también es una constante. Por lo tanto, tenemos tres constantes:
\[\rho_{o}, \overrightarrow{v_{o}}=0, S_{o}\]
Dado que la densidad, la velocidad y la entropía son constantes para una solución homogénea, podemos construir estas cantidades para una solución no homogénea expandiéndonos alrededor de ellas:
\[\begin{aligned} \rho=\rho_{o}+\delta \rho \\ S=S_{o}+\delta S \\ \vec{v} \end{aligned}\]
También podemos expandirnos alrededor de una temperatura y presión constantes:
\[\begin{aligned} &T=T_{o}+\delta T \\ &P=P_{o}+\delta P \end{aligned}\]
Comience sustituyendo la expansión de densidad en la ecuación de continuidad de densidad
\[\begin{aligned} \frac{d}{d t}\left(\rho_{o}+\delta \rho\right)+\vec{\nabla} \cdot\left[\left(\rho_{o}+\delta \rho\right) \vec{v}\right]=0 \\ \frac{d \delta \rho}{d t}+\vec{\nabla} \cdot\left(\rho_{o} \vec{v}\right)=0 \end{aligned}\]
Esta es la ecuación de continuidad de densidad numérica linealizada. Para llegar a la expresión final, hemos utilizado eso\(\frac{d \rho_{o}}{d t}=0\). También hemos ignorado el término\(\vec{\nabla} \cdot(\delta \rho \vec{v})\) porque es de orden cuadrático y podemos suponer que es despreciable. Para linealizar la ecuación de continuidad para la entropía, comience por expandir la expresión original.
\[\rho \frac{\partial \delta s}{\partial t}+s_{o} \frac{\partial \rho}{\partial t}+s_{o} \vec{\nabla} \cdot(\rho \vec{v})+\rho \vec{\nabla} \cdot(\delta s \vec{v})-\lambda \vec{\nabla} \cdot\left(\frac{\vec{\nabla} T}{T}\right)=0\]
El segundo y tercer término se pueden combinar y pasarán a cero por conservación de masa. El cuarto término es despreciable. Luego, sustituyendo en las expansiones y manteniendo solo los términos lineales, la expresión se simplifica para:
\[\rho_{o} \frac{\partial \delta s}{\partial t}-\frac{\lambda}{T_{o}} \nabla^{2} \delta T=0\]
De igual manera podemos linealizar la ecuación de continuidad del momentum, la solución es
\[m \rho_{o} \frac{\partial \vec{v}}{\partial t}+\vec{\nabla} \delta P=\left(\frac{1}{3} \eta+\eta_{B}\right)(\vec{\nabla}: \vec{\nabla}) \cdot \vec{v}+\eta \nabla^{2} \vec{v}\]
En resumen, las ecuaciones hidrodinámicas linealizadas vienen dadas por
\[\begin{aligned} \frac{d \delta \rho}{d t}+\rho_{o} \vec{\nabla} \cdot \vec{v} &=0 \\ m \rho_{o} \frac{\partial \vec{v}}{\partial t}+\nabla \delta P &=\left(\frac{1}{3} \eta+\eta_{B}\right)(\vec{\nabla}: \vec{\nabla}) \cdot \vec{v}+\eta \nabla^{2} \vec{v} \\ \rho_{o} \frac{\partial \delta s}{\partial t}-\frac{\lambda}{T_{o}} \nabla^{2} \delta T &=0 \end{aligned}\]
Modos hidrodinámicos transversales
Para resolver la ecuación del valor propio, necesitamos descomponer la velocidad en sus componentes transversales y longitudinales. Comience por reescribir la velocidad en términos de sus componentes de Fourier
\[\vec{v}(r, t)=\frac{1}{(2 \pi)^{3}} \int \vec{v}(k, t) e^{i \vec{k} \cdot \vec{r}} d \vec{k}\]
A través de la sustitución, la ecuación de continuidad de impulso se
\[m \rho_{o} \frac{\partial \overrightarrow{v_{k}}}{\partial t}+i \vec{k} P_{k}=\left(\frac{1}{3} \eta+\eta_{B}\right)(i \vec{k})\left(i \vec{k} \cdot \overrightarrow{v_{k}}\right)+\eta(\vec{k})^{2} \overrightarrow{v_{k}}\]
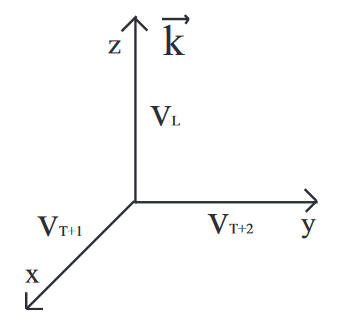
Ahora, descomponerse\(\vec{v}(k, t)\) en sus 3 componentes
\[v(k, t)=v_{x k}(t) \hat{x}+v_{y k}(t) \hat{y}+v_{z k}(t) \hat{z}\]
Un modo longitudinal es aquel en el que el vector de velocidad apunta paralelo al\(\vec{k}\) vector, y un modo transversal es aquel en el que el vector de velocidad apunta perpendicular al\(\vec{k}\) vector. Podemos decidir arbitrariamente que el\(\vec{k}\) vector apunta en la\(z\) dirección. Por lo tanto,\(v_{z k}(t)\) es la corriente longitudinal\(v_{x k}(t)\) y y\(v_{y k}(t)\) son las corrientes transversales.
que es fácil de resolver, dando la solución
\[v_{T k}(t)=v_{T k}(0) e^{-\gamma_{T} k^{2} t}\]
donde\(\gamma_{T}=\frac{\eta}{m \rho_{o}}\) está la viscosidad cinemática de cizallamiento.
Este resultado parece una ecuación de difusión
\[\frac{\partial P_{k}}{\partial t}=-D k^{2} P_{k}\]
Por lo tanto, se\(\gamma_{T}\) puede interpretar como constante de difusión para la velocidad.
Modos hidrodinámicos longitudinales
Resolviendo las ecuaciones de continuidad
Es mucho más difícil de resolver para el componente de velocidad longitudinal de la corriente porque no tantos términos van a cero.
Transformada de Fourier de la densidad Comience por escribir la densidad en términos de sus componentes de Fourier
\[\vec{\rho}(r, t)=\frac{1}{(2 \pi)^{3}} \int \vec{\rho}(k, t) e^{i \vec{k} \vec{r}} d \vec{k}\]
Usando esta expresión, las ecuaciones hidrodinámicas linealizadas se pueden escribir en términos de los componentes de Fourier de la densidad. Tenga en cuenta que en adelante, por brevedad, dejaremos caer los\(\delta\) signos de las variables transformadas. Los lectores deben tener en cuenta que estas variables\(k\) -espacio siempre se refieren a la transformada de Fourier de las fluctuaciones alejadas del equilibrio.
\[\begin{aligned} \frac{d \rho_{k}}{d t}+i k \rho_{o} v_{k} &=0 \\ m \rho_{o} \frac{\partial v_{k}}{\partial t}+i k P_{k}+\left(\frac{4}{3} \eta+\eta_{B}\right) k^{2} v_{k} &=0 \\ \rho_{o} \frac{\partial s_{k}}{\partial t}+\frac{\lambda}{T_{o}} k^{2} T_{k} &=0 \end{aligned}\]
También denotamos la velocidad en\(v_{k}\) cuanto a la simplicidad. No obstante, es importante recordar que esto sólo se refiere a la velocidad longitudinal,\(v_{z, k}\). Elección de variables independientes Como está escrito, las tres ecuaciones de continuidad tienen cinco variables:\(\rho_{k}, v_{k}, T_{k}, P_{k}\), y\(S_{k}\). Por suerte, estas variables no son todas independientes. Dejar\(\rho_{k}, v_{k}\), y\(T_{k}\) ser las tres variables independientes. Podemos usar relaciones termodinámicas para reescribir\(P_{k}\) y\(S_{k}\) en términos de estas variables.
La energía libre de Helmholtz es una función de la temperatura y la densidad,\(F(T, \rho)\). Podemos escribir esto en forma diferencial:
\[d F=-S d T+P d \rho\]
Este es un diferencial total de la forma:
\[d z=\left(\frac{\partial z}{\partial x}\right)_{y} d x+\left(\frac{\partial z}{\partial y}\right)_{x} d y\]
Usando esto, podemos escribir la entropía\(S\) y la presión\(P\) en forma diferencial
\[\begin{aligned} S=-\left(\frac{\partial F}{\partial T}\right)_{\rho} \\ P=\left(\frac{\partial F}{\partial \rho}\right)_{T} \end{aligned}\]
Definir la variable\(\alpha\) como
\[\alpha=\left(\frac{\partial P}{\partial T}\right)_{\rho}=\frac{\partial}{\partial T}\left(\frac{\partial F}{\partial \rho}\right)_{T}=\frac{\partial}{\partial \rho}\left(\frac{\partial F}{\partial T}\right)_{\rho}=-\left(\frac{\partial S}{\partial \rho}\right)_{T}\]
Aquí hemos utilizado la propiedad de que para funciones continuas, las segundas derivadas parciales mixtas son iguales. Esto da una de las relaciones Maxwell.
También utilizaremos un par de relaciones bien conocidas, la velocidad isotérmica del sonido:
\[c_{T}=\sqrt{\frac{1}{m}\left(\frac{\partial P}{\partial \rho}\right)_{T}}\]
y el calor específico:
\[C_{V}=T\left(\frac{\partial S}{\partial T}\right)_{\rho}\]
Con estas relaciones en la mano, podemos reescribir la presión\(P\) y la entropía\(S\) en términos de temperatura\(T\) y densidad\(\rho\):
\[\begin{aligned} d P=\left(\frac{\partial P}{\partial \rho}\right)_{T} d \rho+\left(\frac{\partial P}{\partial T}\right)_{\rho} d T=m C_{T}^{2} d \rho+\alpha d T \\ T_{o} d S=T_{o}\left(\frac{\partial S}{\partial \rho}\right)_{T} d \rho+T_{o}\left(\frac{\partial S}{\partial T}\right)_{\rho} d T=-T_{o} \alpha d \rho+C_{V} d T \end{aligned}\]
Las ecuaciones condensadas Con estas sustituciones, podemos reescribir las ecuaciones de continuidad en términos de las variables independientes\(\rho_{k}, v_{k}\), y\(T_{k}\).
\[\begin{aligned} \frac{d \rho_{k}}{d t}+i k \rho_{o} v_{k} &=0 \\ \dot{v}_{k}+\frac{i k}{m \rho_{o}}\left[C_{T}^{2} m \rho_{k}+\alpha T_{k}\right]+b k^{2} v_{k} &=0 \\ \dot{T}_{k}+i k\left(\frac{T_{o} \alpha \rho_{o}}{C_{V}}\right) v_{k}+a k^{2} T_{k} &=0 \end{aligned}\]
donde hemos definido las constantes\(a\) y\(b\)
\[\begin{aligned} a=\frac{\lambda}{\rho_{o} C_{V}} \\ b=\left(\eta_{B}+\frac{4}{3} \eta\right) \frac{1}{m \rho_{o}} \end{aligned}\]
y\(\rho_{k}=-i k \rho_{o} v_{k}\) se utiliza para simplificar la última ecuación.
La transformación de Laplace Para simplificar aún más las ecuaciones, use la transformada de Laplace de cada variable:
\[\begin{array}{llll} \hat{\rho}_{k}(z)=\int_{0}^{\infty} e^{-z t} \rho_{k}(t) d t & \text { and } & \rho_{k}(t)=\frac{1}{2 \pi i} \int_{\delta-i \infty}^{\delta+i \infty} e^{z t} \hat{\rho}_{k}(z) d z \\ \hat{v}_{k}(z)=\int_{0}^{\infty} e^{-z t} v_{k}(t) d t & \text { and } & v_{k}(t)=\frac{1}{2 \pi i} \int_{\delta-i \infty}^{\delta+i \infty} e^{z t} \hat{v}_{k}(z) d z \\ \hat{T}_{k}(z)=\int_{0}^{\infty} e^{-z t} T_{k}(t) d t \quad \text { and } & T_{k}(t)=\frac{1}{2 \pi i} \int_{\delta-i \infty}^{\delta+i \infty} e^{z t} \hat{T}_{k}(z) d z \end{array}\]
Usando esta transformación, las ecuaciones de continuidad se pueden reescribir (en forma de matriz):
\[\left[\begin{array}{ccc} z & i k \rho_{o} & 0 \\ i k \frac{C_{T}^{2}}{\rho_{o}} & z+b k^{2} & \frac{i k}{m \rho_{o}} \alpha \\ 0 & \frac{i k}{C_{V}} \alpha T_{o} \rho_{o} & z+a k^{2} \end{array}\right]=\left[\begin{array}{c} \hat{\rho}_{k} \\ \hat{v}_{k} \\ \hat{T}_{k} \end{array}\right]=\left[\begin{array}{c} \rho_{k}(0) \\ v_{k}(0) \\ T_{k}(0) \end{array}\right] .\]
Identidades termodinámicas
Velocidad isotérmica y adiabática del sonido
Las\(c_{T}\) velocidades adiabáticas\(c_{s}\) e isotérmicas del sonido vienen dadas por:
\[\begin{aligned} c_{S}^{2}=\frac{1}{m}\left(\frac{\partial P}{\partial \rho}\right)_{S} \\ c_{T}^{2}=\frac{1}{m}\left(\frac{\partial P}{\partial \rho}\right)_{T} \end{aligned}\]
Podemos reescribir estas cantidades usando:
\[\left(\frac{\partial P}{\partial \rho}\right)_{T}=\frac{\left(\frac{\partial P}{\partial S}\right)_{T}}{\left(\frac{\partial \rho}{\partial S}\right)_{T}}=\frac{\left(\frac{\partial P}{\partial T}\right)_{S}\left(\frac{\partial T}{\partial S}\right)_{P}}{\left(\frac{\partial \rho}{\partial T}\right)_{S}\left(\frac{\partial T}{\partial S}\right)_{\rho}}=\frac{C_{V}}{C_{P}}\left(\frac{\partial P}{\partial \rho}\right)_{S}\]
Aquí, hemos utilizado las capacidades de\(C_{P}\) calor de volumen constante\(C_{V}\) y presión constante:
\[\begin{aligned} &C_{V}=T\left(\frac{\partial S}{\partial T}\right)_{\rho} \\ &C_{P}=T\left(\frac{\partial S}{\partial T}\right)_{P} \end{aligned}\]
y la identidad para los diferenciales:
\[\left(\frac{\partial x}{\partial y}\right)_{z}=\left(\frac{\partial x}{\partial z}\right)_{y}\left(\frac{\partial z}{\partial y}\right)_{x}\]
Ahora, podemos demostrar que la relación es igual a:
\[\frac{c_{T}^{2}}{c_{S}^{2}}=\frac{\frac{1}{m} \frac{C_{V}}{C_{P}}\left(\frac{\partial P}{\partial \rho}\right)_{S}}{\frac{1}{m}\left(\frac{\partial P}{\partial \rho}\right)_{S}}=\frac{C_{V}}{C_{P}}=\frac{1}{\gamma}\]
Las identidades termodinámicas se pueden utilizar para reescribir la cantidad
\[m C_{T}^{2}\left(C_{P}-C_{V}\right)\]
Comience por escribir la expresión explícitamente en términos de variables termodinámicas:
\[m C_{T}^{2}\left(C_{P}-C_{V}\right)=T\left(\frac{\partial P}{\partial \rho}\right)_{T}\left[\left(\frac{\partial S}{\partial T}\right)_{P}-\left(\frac{\partial S}{\partial T}\right)_{\rho}\right]\]
Para simplificar esta expresión, usaremos otra identidad para diferenciales:
\[\left(\frac{\partial x}{\partial y}\right)_{z}=\left(\frac{\partial x}{\partial y}\right)_{w}+\left(\frac{\partial x}{\partial w}\right)_{y}\left(\frac{\partial w}{\partial y}\right)_{z}\]
Usando esta identidad, combinada con la identidad introducida en la sección anterior, podemos reescribir el primer término en la expresión:
\[\left(\frac{\partial S}{\partial T}\right)_{P}=\left(\frac{\partial S}{\partial T}\right)_{\rho}+\left(\frac{\partial S}{\partial \rho}\right)_{T}\left(\frac{\partial \rho}{\partial T}\right)_{P}=\left(\frac{\partial S}{\partial T}\right)_{\rho}-\left(\frac{\partial S}{\partial \rho}\right)_{T}\left(\frac{\partial \rho}{\partial P}\right)_{T}\left(\frac{\partial P}{\partial T}\right)_{\rho}\]
Ahora, conecte esto a la expresión anterior y cancele términos, para obtener la nueva identidad:
\[m C_{T}^{2}\left(C_{P}-C_{V}\right)=-T_{o}\left(\frac{\partial S}{\partial \rho}\right)_{T}\left(\frac{\partial P}{\partial T}\right)_{\rho}\]
Compresibilidad adiabática e isotérmica
Las\(\chi_{T}\) compresibilidades adiabáticas\(\chi_{S}\) e isotérmicas vienen dadas por:
\[\begin{aligned} \chi_{S} &=\frac{1}{\rho}\left(\frac{\partial \rho}{\partial P}\right)_{S} \\ \chi_{T} &=\frac{1}{\rho}\left(\frac{\partial \rho}{\partial P}\right)_{T} \end{aligned}\]
Por lo tanto,
\[\gamma=\frac{C_{P}}{C_{V}}=\frac{\chi_{T}}{\chi_{S}}=\frac{c_{S}^{2}}{c_{T}^{2}}\]
Eigensolution
Ahora, podemos resolver el conjunto de ecuaciones de continuidad para la densidad. La densidad se puede encontrar a partir de:
\[\hat{\rho}(z)=\frac{\operatorname{Det}^{\prime} M(1 \mid 1)}{\operatorname{Det} M}=\left(M^{-1}\right)_{11} \rho(0)\]
Tenga en cuenta que la transformada de Laplace de la función de dispersión intermedia es:
\[\hat{F}(\vec{k}, z)=\left(M^{-1}\right)_{11}\left\langle\left|\rho_{k}\right|^{2}\right\rangle\]
Para resolver para\(\hat{\rho}(z)\), encontrar\(\operatorname{Det}^{\prime} M(1 \mid 1)\) y\(\operatorname{Det} M\).
\[\begin{aligned} \operatorname{Det}^{\prime} M(1 \mid 1)=\left(z+a k^{2}\right)\left(z+b k^{2}\right)+\frac{k^{2} T_{o} \alpha^{2}}{m C_{V}} \\ =\left(z+a k^{2}\right)\left(z+b k^{2}\right)+k^{2} C_{T}^{2}(\gamma-1) \end{aligned}\]
y
\[\text { Det } M=z\left(z+a k^{2}\right)\left(z+b k^{2}\right)+z k^{2} c_{S}^{2}+z k^{4} c_{T}^{2}\]
donde hemos utilizado algunas de las identidades termodinámicas definidas en la sección anterior.
Las frecuencias propias se pueden obtener de\(\operatorname{Det} M(z)=0\). Los valores propios se pueden resolver mediante perturbación\(z=s_{o}+s_{1} k+s_{2} k+\ldots\). Las soluciones son
\[\begin{aligned} z_{\pm}=-a \frac{c_{T}^{2}}{c_{S}^{2}} k^{2}=-\frac{a}{T} k^{2} \\ z_{\pm}=\pm i c_{S} k-\Gamma k^{2} \end{aligned}\]
donde
\[\Gamma=\frac{1}{2}\left[(a+b)-\frac{a}{\gamma}\right]\]
A primer orden en\(k\), tenemos
\[\left(M^{-1}\right)_{11}=\frac{\operatorname{Det}^{\prime} M(1 \mid 1)}{\operatorname{Det} M} \approx \frac{z^{2}+\left(1-\frac{1}{\gamma}\right) c_{S}^{2} k^{2}}{z^{3}+z k^{2} c_{S}^{2}}=\left(1-\frac{1}{\gamma}\right) \frac{1}{z}+\frac{1}{\gamma} \frac{1}{z^{2}+k^{2} c_{S}^{2}}\]
Entonces, a segundo orden en\(k\), tenemos
\[\hat{\rho}_{k}(t)=\hat{\rho_{k}}(0)\left[\left(1-\frac{1}{\gamma}\right) e^{-\frac{a}{\gamma} k^{2} t}+\frac{1}{\gamma} \cos \left(c_{S} k t\right) e^{-\Gamma k^{2} t}\right]\]
El primer término da las contribuciones de las fluctuaciones térmicas, mientras que el segundo término da la solución para una onda acústica amortiguada. Observe que la intensidad integrada del primer término es\(\left(1-\frac{1}{\gamma}\right)\) y la intensidad integrada del segundo término lo es\(\frac{1}{\gamma}\).
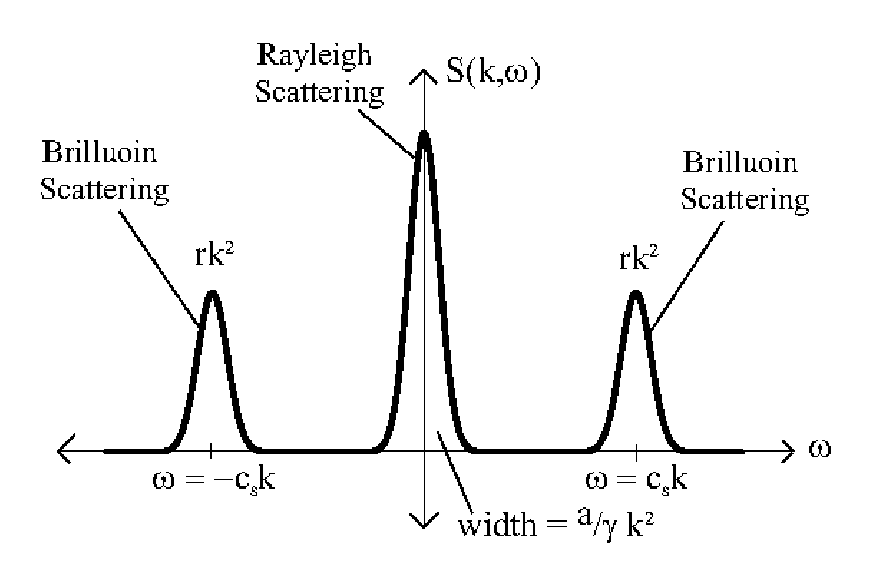
Dispersión de luz
La relación Landau-Placzek da la relación entre la intensidad de dispersión térmica y acústica
\[\frac{I_{\text {thermal }}}{I_{\text {acoustic }}}=\frac{\left\langle(\delta \rho)^{2}\right\rangle_{\text {thermal }}}{\left\langle(\delta \rho)^{2}\right\rangle_{\text {mech }}}=\frac{\left(\frac{\partial \rho}{\partial S}\right)_{P}^{2}\left\langle\Delta S^{2}\right\rangle}{\left(\frac{\partial \rho}{\partial P}\right)_{S}^{2}\left\langle\Delta P^{2}\right\rangle}=\frac{C_{P}-C_{V}}{C_{V}}=\gamma-1\]
Obsérvese que el factor de estructura dinámica es el doble de la parte real de la transformada de Laplace de la función de dispersión intermedia (Figura 3.9):
\[S(\vec{k}, \omega)=\int_{\infty}^{\infty} F(\vec{k}, t) e^{-i \omega t} d t=2 \operatorname{Re} \hat{F}(z=-i \omega)\]
El valor inicial de esta función es
\[F(k, 0)=\frac{1}{N}\left\langle\left|\delta \rho_{k}\right|^{2}\right\rangle=\rho_{o} h+1=\frac{\rho_{o} \chi_{T}}{\beta}\]
Dispersión Acústica
Al ignorar el acoplamiento al flujo de entropía, tenemos
\[d P=\left(\frac{\partial P}{\partial \rho}\right)_{S} d \rho\]
para que
\[\begin{array}{r} \frac{d \delta \rho_{k}}{d t}+i k \rho_{o} v_{k}=0 \\ \dot{v_{k}}+i c_{S}^{2} k \rho_{k}+b k^{2} v_{k}=0 \end{array}\]
Para un gas ideal,\(b=0\), y así conseguimos una onda de sonido que se propaga
\[z=\pm i c_{S} k\]
En un líquido viscoso,\(b \neq 0\), y así obtenemos una onda acústica que se propaga con un término de amortiguación
\[z=\pm i c_{S} k-\frac{1}{2} b k^{2}\]


