2.3: La teoría molecular cinética de los gases

Los modelos teóricos que intentan describir la naturaleza de los gases se remontan a las primeras investigaciones científicas sobre la naturaleza de la materia ¡e incluso antes! Alrededor del 50 a.C., Lucrecio, filósofo romano, propuso que los cuerpos macroscópicos estaban compuestos por átomos que chocan continuamente entre sí y están en constante movimiento, a pesar de la realidad observable de que el cuerpo mismo es como reposo. Sin embargo, las ideas de Lucrecio fueron ignoradas en gran medida, ya que se desviaron de las de Aristóteles, cuyos puntos de vista fueron más ampliamente aceptados en ese momento.

En 1738, Daniel Bernoulli (Bernoulli, 1738) publicó un modelo que contiene el marco básico para la moderna teoría cinética molecular. Rudolf Clausius amplió el modelo en 1857 introduciendo (entre otras cosas) el concepto de camino libre medio (Clausius, 1857). Estas ideas fueron desarrolladas aún más por Maxwell (Maxwell, Molecules, 1873). Pero, debido a que la teoría atómica no se abrazó completamente a principios del ^siglo XX, no fue hasta que Albert Einstein publicó una de sus obras seminales describiendo el movimiento browniano (Einstein, 1905) en la que modeló la materia usando una teoría cinética de moléculas que la idea de un atómico (o molecular) foto realmente se afianzó en la comunidad científica.

En su forma moderna, la Teoría Cinética Molecular de los gases se basa en cinco postulados básicos.

1. Las partículas de gas obedecen las leyes de movimiento de Newton y viajan en líneas rectas a menos que choquen con otras partículas o con las paredes del contenedor.
2. Las partículas de gas son muy pequeñas en comparación con los promedios de las distancias entre ellas.
3. Las colisiones moleculares son perfectamente elásticas para que se conserve la energía cinética.
4. Las partículas de gas no interactúan con otras partículas excepto a través de colisiones. No hay fuerzas atractivas ni repulsivas entre las partículas.
5. La energía cinética promedio de las partículas en una muestra de gas es proporcional a la temperatura.

Cualitativamente, este modelo predice la forma de la ley de gas ideal.

1. Más partículas significa más colisiones con la pared (\(p \propto n\))
2. Un volumen más pequeño significa colisiones más frecuentes con la pared (\(p \propto 1/V\))
3. Velocidades moleculares más altas significan colisiones más frecuentes con las paredes (\(p \propto T\))

Al juntar todos estos rendimientos

\[ p \propto \dfrac{nT}{V} =k \dfrac{nT}{V}\]

¡que es exactamente la forma de la ley de gas ideal! El resto del trabajo consiste en derivar un valor para la constante de proporcionalidad (\(k\)) que sea consistente con la observación experimental.

Para simplificar, imagine una colección de partículas de gas en un contenedor de volumen fijo con todas las partículas viajando a la misma velocidad. ¿Qué implicaciones tendría la teoría molecular cinética en una muestra de este tipo? Un enfoque para responder a esta pregunta es derivar una expresión de la presión del gas.

La presión se va a determinar considerando las colisiones de moléculas de gas con la pared del contenedor. Cada colisión impartirá algo de fuerza. Entonces, cuanto mayor sea el número de colisiones, mayor será la presión. Además, cuanto mayor sea la fuerza impartida por colisión, mayor será la presión. Y finalmente, cuanto mayor sea el área sobre la que se propagan las colisiones, menor será la presión.

\[ p \propto \dfrac{ (\text{number of collisions}) \times (\text{force imparted per collision})}{area}\]

Figura\(\PageIndex{1}\): El “volumen de colisión” es el subconjunto del volumen total que contiene moléculas que realmente colisionarán con el área\(A\) en el intervalo de tiempo\(\Delta t\).

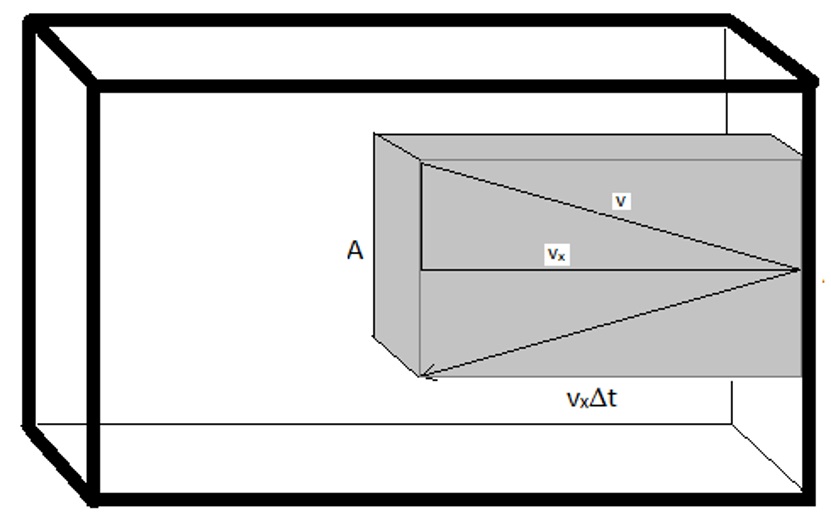
En primer lugar, la presión que ejerce el gas sobre las paredes del contenedor se debe enteramente a la fuerza impartida cada vez que una molécula choca con la superficie interior del contenedor. Esta fuerza se escalará por el número de moléculas que golpeen el área de la pared en un tiempo dado. Por esta razón, es conveniente definir un “volumen de colisión”.

\[ V_{col}= (v_x \cdot \Delta t) \cdot A\]

donde\(v_x\) está la velocidad que las moléculas están viajando en la dirección x,\(\Delta t\) es el intervalo de tiempo (el producto de\(v_x·\Delta T\) da la longitud a la caja de volumen de colisión) y A es el área de la pared con la que colisionarán las moléculas. La mitad de las moléculas dentro de este volumen chocarán con la pared ya que la mitad viajará hacia ella y la otra mitad viajará lejos de ella. El número de moléculas en este volumen de colisión vendrá dado por el número total de moléculas en la muestra y la fracción del volumen total que es el volumen de colisión. Y así, el número de moléculas que colisionarán con la pared viene dado por

\[ N_{col} =\dfrac{1}{2} N_{tot} \dfrac{V_{col}}{V}\]

Y así el número de moléculas que chocan con la pared será

\[ N_{col} =\dfrac{1}{2} N_{tot} \dfrac{(v_x \cdot \Delta t) \cdot A}{V}\]

La magnitud de esa fuerza impartida por colisión estará determinada por la velocidad de cambio de momento de cada partícula a medida que golpea la superficie. Se puede calcular determinando el cambio de impulso total y dividiendo por el tiempo total requerido para el evento. Dado que cada molécula colisionante cambiará su velocidad de v _x a —v _x, la magnitud del cambio de momento es de 2 (mv _x). Así, la fuerza impartida por colisión viene dada por

\[ F = \dfrac{2(mv_x)}{\Delta t}\]

y la fuerza total impartida es

\[\begin{align} F_{tot} &= N_{col} \dfrac{2 (mv_x)}{\Delta t} \\[4pt] &= \dfrac{1}{2} N_{tot} \left[ \dfrac{(v_x\Delta t)A}{V} \right] \left[ \dfrac{2(m v_x)}{\Delta t} \right] \\[4pt] &= N_{tot} \left(\dfrac{mv_x^2}{V} \right) A \end{align}\]

Dado que la presión se da como la fuerza total ejercida por unidad de área, la presión viene dada por

\[p = \dfrac{F_{tot}}{A} = N_{tot} \left( \dfrac{mv_x^2}{V} \right) = \dfrac{N_{tot}m}{V} v_x^2\]

La pregunta entonces se convierte en cómo lidiar con el término velocidad. Inicialmente, se asumió que todas las moléculas tenían la misma velocidad, por lo que la magnitud de la velocidad en la dirección x era meramente una función de la trayectoria. Sin embargo, las muestras reales de gases comprenden moléculas con una distribución completa de velocidades moleculares y trayectorias. Para hacer frente a esta distribución de valores, reemplazamos (\(v_x^2\)) con el promedio cuadrado de velocidad en la dirección x\(\langle v_x \rangle ^2\).

\[p = \dfrac{N_{tot}m}{V} \langle v_x \rangle ^2 \label{press}\]

La función de distribución para velocidades en la dirección x, conocida como distribución Maxwell-Boltzmann, viene dada por:

\[f(v_x) = \underbrace{\sqrt{ \dfrac{m}{2\pi k_BT} }}_{\text{normalization term}} \underbrace{\exp \left(\dfrac{-mv_x^2}{2k_BT} \right)}_{\text{exponential term}}\]

Esta función tiene dos partes: una constante de normalización y un término exponencial. La constante de normalización se deriva al señalar que

\[\int _{-\infty}^{\infty} f(v_x) dv_x =1 \label{prob}\]

Normalización de la distribución Maxwell-Boltzmann

La distribución Maxwell-Boltzmann tiene que normalizarse porque es una distribución de probabilidad continua. Como tal, la suma de las probabilidades para todos los valores posibles de v _x debe ser unidad. Y dado que\(v_­x\) puede tomar cualquier valor entre -∞ y ∞, entonces la Ecuación\ ref {prob} debe ser verdadera. Entonces, si\(f(v_x)\) se supone que la forma de

\[f(v_x) = N \exp - \left(\dfrac{mv_x^2}{2k_BT} \right)\]

La constante de normalización se\(N\) puede encontrar en

\[ \int_{-\infty}^{\infty} f(v_x) dv_x = \int_{-\infty}^{\infty} N \exp \left(\dfrac{-mv_x^2}{2k_BT} \right) dv_x =1\]

La expresión se puede simplificar dejando\(\alpha = m/2k_BT\). Entonces se escribe de manera más simple

\[ N \int_{-\infty}^{\infty} \exp \left(\dfrac{-mv_x^2}{2k_BT} \right) dv_x =1\]

Una tabla de integrales definidas dice que

\[ \int_{-\infty}^{\infty} e^{- a x^2} dx = \sqrt{\dfrac{\pi}{a}}\]

Entonces

\[ N \sqrt{\dfrac{\pi}{\alpha}} = \left( \dfrac{m}{2\pi k_BT} \right) ^{1/2}\]

Y así la función de distribución normalizada viene dada por

\[ f(v_x) = \left( \dfrac{m}{2\pi k_BT} \right) ^{1/2} \text{exp} \left( \dfrac{m v_x^2}{2 k_BT} \right) \label{MB}\]

Calcular un promedio a partir de una distribución de probabilidad

Calcular un promedio para un conjunto finito de datos es bastante fácil. El promedio se calcula por

\[ \bar{x} = \dfrac{1}{N} \sum_{i=1}^N x_i\]

Pero, ¿cómo se procede cuando el conjunto de datos es infinito? ¿O cómo procede uno cuando todo lo que uno sabe son las probabilidades para cada posible resultado medido? ¡Resulta que eso también es bastante simple!

\[ \bar{x} = \sum_{i=1}^N x_i P_i\]

donde\(P_i\) está la probabilidad de medir el valor\(x_i\). Esto también se puede extender a problemas donde las propiedades medibles no son discretas (como los números que resultan de rodar un par de dados) sino que provienen de una población parental continua. En este caso, si la probabilidad es de medir un resultado específico, el valor promedio puede ser determinado por

\[\bar{x} = \int x P(x) dx\]

donde\(P(x)\) es la función que describe la distribución de probabilidad, y con la integración teniendo lugar a través de todos los valores posibles que x puede tomar.

Calcular el valor promedio de\(v_x\)

Un valor que es útil (y se utilizará en desarrollos posteriores) es la velocidad promedio en la dirección x. Esto se puede derivar usando la distribución de probabilidad, como se muestra en el cuadro de desarrollo matemático anterior. El valor promedio de\(v_x\) viene dado por

\[ \langle v_x \rangle = \int _{-\infty}^{\infty} v_x (f(v_x) dx\]

Esta integral será, por necesidad, cero. Este debe ser el caso ya que la distribución es simétrica, de manera que la mitad de las moléculas se desplazan en la dirección +x, y la mitad en la dirección —x. Estas mociones tendrán que cancelar. Entonces, se dará un resultado más satisfactorio al considerar la magnitud de\(v_x\), lo que da la velocidad en la dirección x. Dado que esto no puede ser negativo, y dada la simetría de la distribución, el problema se vuelve

\[ \langle |v_x |\rangle = 2 \int _{0}^{\infty} v_x (f(v_x) dx\]

Es decir, consideraremos sólo la mitad de la distribución, para luego duplicar el resultado para dar cuenta de la mitad que ignoramos.

Por simplicidad, escribiremos la función de distribución como

\[ f(v_x) = N \exp(-\alpha v_x^2)\]

donde

\[ N= \left( \dfrac{m}{2\pi k_BT} \right) ^{1/2} \]

y

\[\alpha = \dfrac{m}{2k_BT}.\]

Una tabla de integrales definidas muestra

\[ \int_{0}^{\infty} x e^{- a x^2} dx = \dfrac{1}{2a}\]

por lo

\[ \langle v_x \rangle = 2N \left( \dfrac{1}{2\alpha}\right) = \dfrac{N}{\alpha}\]

Sustituir nuestras definiciones por\(N\) y\(\alpha\) producir

\[ \langle v_x \rangle = \left( \dfrac{m}{2\pi k_BT} \right)^{1/2} \left( \dfrac{2 k_BT}{m} \right) = \left( \dfrac{2\pi k_BT}{ \pi m} \right)^{1/2} \]

Esta expresión indica la velocidad promedio para el movimiento de en una dirección.

Sin embargo, las muestras de gas reales tienen moléculas no solo con una distribución de velocidades moleculares y también una distribución aleatoria de direcciones. Usando propiedades de magnitud vectorial normal (o simplemente usando el Teorema de Pitágoras), se puede ver que

\[ \langle v \rangle^2 = \langle v_x \rangle^2 + \langle v_y \rangle^2 + \langle v_z \rangle^2\]

Dado que la dirección de desplazamiento es aleatoria, la velocidad puede tener cualquier componente en las direcciones x, y o z con igual probabilidad. Como tal, el valor promedio de los componentes x, y o z de velocidad debe ser el mismo. Y así

\[ \langle v \rangle^2 = 3 \langle v_x \rangle^2\]

Sustituyendo esto en la expresión de presión (Ecuación\ ref {press}) rinde

\[ p =\dfrac{ N_{tot}m}{3V} \langle v \rangle^2\]

Todo lo que queda es determinar la forma de distribución de las magnitudes de velocidad que pueden tomar las moléculas de gas. Una de las primeras personas en abordar esta distribución fue James Clerk Maxwell (1831-1879). En su artículo de 1860 (Maxwell, Ilustraciones de la teoría dinámica de los gases. Parte 1. Sobre los movimientos y colisiones de esferas perfectamente elásticas, 1860), propuso una forma para esta distribución de velocidades que demostró ser consistente con las propiedades observadas de los gases (como sus viscosidades). Derivó esta expresión a partir de una transformación del sistema de coordenadas de coordenadas cartesianas (\(x\),\(y\),\(z\)) a coordenadas polares esféricas (\(v\),\(\theta\),\(\phi\)). En este nuevo sistema de coordenadas, v representa la magnitud de la velocidad (o la velocidad) y todos los datos direccionales se transportan en los ángulos\(\theta\) y\(\phi\). La unidad de volumen infinitesimal se convierte

\[ dx\,dy\,dz\, = v^2 \sin( \theta) \,dv\,d\theta \,d\phi\]

Aplicando esta transformación de coordenadas, e ignorando la parte angular (ya que solo le interesaba la velocidad) la distribución de Maxwell (Ecuación\ ref {MB}) tomó la siguiente forma

\[ f(v) = N v^2 \text{exp} \left( \dfrac{m v^2}{2 k_BT} \right) \label{MBFullN}\]

Esta función tiene tres partes básicas: una constante de normalización (\(N\)), una dependencia de la velocidad (\(v^2\)) y un término exponencial que contiene la energía cinética (\(½ mv^2\)). Dado que la función representa la fracción de moléculas con la velocidad\(v\), la suma de las fracciones para todas las velocidades posibles debe ser la unidad. Esta suma se puede calcular como una integral. La constante de normalización asegura que

\[ \int_0^{\infty} f(v) dv = 1\]

Elegir la constante de normalización como

\[ N =4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 }\]

produce la forma final de la distribución Maxwell de velocidades moleculares.

\[ N =4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } v^2 \text{exp} \left( \dfrac{m v^2}{2 k_BT} \right) \label{MBFull}\]

A bajas velocidades, el\(v^2\) término hace que la función aumente al aumentar\(v\), pero luego a valores mayores de\(v\), el término exponencial hace que vuelva a caer asintóticamente a cero. La distribución se extenderá sobre un mayor rango de velocidad a temperaturas más altas, pero colapsará a un rango menor de valores a temperaturas más bajas (Cuadro 2.3.1).

Figura 2.3.1: Distribución Maxwell de velocidades para moléculas de hidrógeno a diferentes temperaturas.

Cálculo de la Velocidad Media

Usando la distribución Maxwell como distribución de probabilidades, se puede determinar la velocidad molecular promedio en una muestra de moléculas de gas.

\[ \begin{align} \langle v \rangle & = \int _{-\infty}^{\infty} v \,f(v) dv \\ & = \int _{-\infty}^{\infty} v\, 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } v^2 \text{exp} \left( \dfrac{m v^2}{2 k_BT} \right)\ dv \\ & = 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } \int _{-\infty}^{\infty} v^3 \text{exp} \left( \dfrac{m v^2}{2 k_BT} \right)\ dv \end{align}\]

Lo siguiente se puede encontrar en una tabla de integrales:

\[ \int_0^{\infty} x^{2n+1} e^{-ax^2} dx = \dfrac{n!}{2a^{n+1}}\]

Entonces

\[\langle v \rangle = 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } \left[ \dfrac{1}{2 \left( \dfrac{m}{2 k_B T} \right) ^2 } \right]\]

Lo que simplifica

\[\langle v \rangle = \left( \dfrac{8 k_BT}{\pi m} \right) ^{1/2} \]

Nota: ¡el valor de\(\langle v \rangle \) es el doble del\(\langle v_x \rangle \) que se derivó en un ejemplo anterior!

\[\langle v \rangle = 2\langle v_x \rangle \]

Ejemplo\(\PageIndex{1}\):

¿Cuál es el valor promedio de la velocidad al cuadrado según la ley de distribución Maxwell?

Solución:

\[ \begin{align} \langle v^2 \rangle & = \int _{-\infty}^{\infty} v^2 \,f(v) dv \\ & = \int _{-\infty}^{\infty} v^2\, 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } v^2 \text{exp} \left( \dfrac{m v^2}{2 k_BT} \right)\ dv \\ & = 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } \int _{-\infty}^{\infty} v^4 \text{exp} \left( \dfrac{m v^2}{2 k_BT} \right)\ dv \end{align}\]

Una tabla de integrales indica que

\[ \int_0^{\infty} x^{2n} e^{-ax^2} dx = \dfrac{1 \cdot 3 \,cdot 5 \dots (2n-1)}{2^{n+1}a^n} \sqrt{\dfrac{\pi}{a}}\]

Sustitución (señalando que\(n = 2\)) rinde

\[\langle v^2 \rangle = 4\pi \sqrt{\left( \dfrac{m}{2\pi k_BT} \right) ^3 } \left[ \dfrac{1 \cdot 3}{2^3 \left( \dfrac{m}{2 k_BT} \right) ^2 } \sqrt{\dfrac{\pi}{\left( \dfrac{m}{2 k_BT} \right)}} \right]\]

lo que simplifica

\[\langle v^2 \rangle = \dfrac{3 k_BT}{ m} \]

Nota: La raíz cuadrada de esta velocidad cuadrada promedio se denomina velocidad media cuadrática (RMS) y tiene el valor

\[v_{rms} = \sqrt{ \langle v^2 \rangle } = \left( \dfrac{3 k_BT}{ m} \right)^{1/2}\]

Toda la distribución también se ve afectada por la masa molecular. Para las moléculas más ligeras, la distribución se extiende a través de un rango más amplio de velocidades a una temperatura dada, pero colapsa a un rango más pequeño para las moléculas más pesadas (Cuadro 2.3.2).

Figura 2.3.2: Distribución Maxwell de velocidades a 800 K para diferentes gases de diferentes masas moleculares.

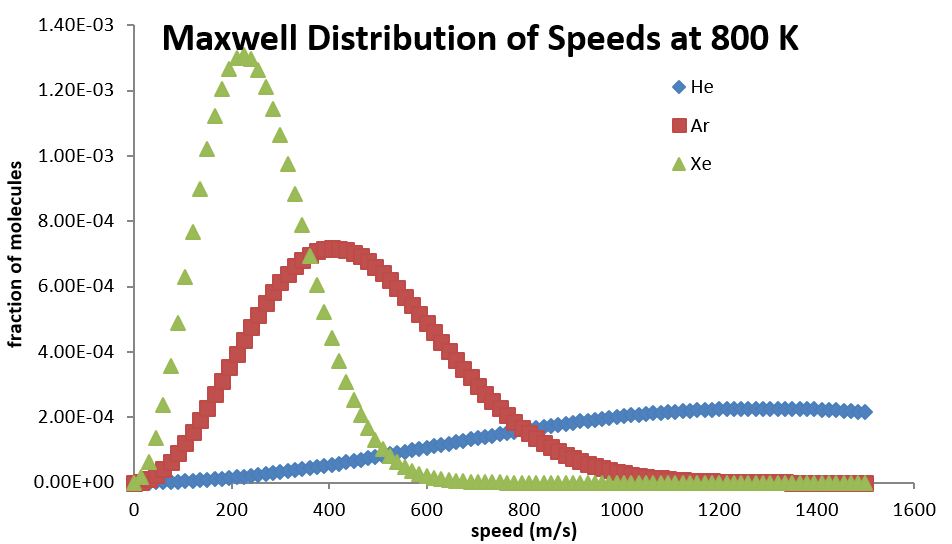
La función de distribución de probabilidad también se puede utilizar para derivar una expresión para las velocidades más probables speed (\(v_{mp}\)\(v_{ave}\)), promedio () y raíz cuadrática media (\(v_{rms}\)) en función de la temperatura y masas de las moléculas en la muestra. La velocidad más probable es la que tiene la probabilidad máxima. Esa será la velocidad que arroje el valor máximo de\(f(v)\). Se encuentra resolviendo la expresión

\[ \dfrac{d}{dv} f(v) = 0\]

por el valor de\(v\) eso lo hace cierto. Este será el valor que dé el valor máximo de\(f(v)\) para la temperatura dada. De igual manera, el valor promedio se puede encontrar utilizando la distribución de la siguiente manera

\[ v_{ave} = \langle v \rangle \]

y la velocidad de raíz cuadrática media (RMS) al encontrar la raíz cuadrada del valor promedio de\(v^2\). Ambos se demostraron arriba.

\[ v_{rms} = \sqrt{ \langle v^2 \rangle} \]